
FYZIKA I •
FYZIKA II •
FYZIKA •
TEORETICKÁ MECHANIKA (TF1) •
KVANTOVÁ TEORIE (TF2)
STATISTICKÁ FYZIKA (TF3) •
VZTAH MATEMATIKY A FYZIKY (TF4) •
OBECNÁ RELATIVITA (TF4)
ELEKTROMAGNETICKÉ POLE (TF4) •
FYZIKA PLAZMATU •
ASTROFYZIKA •
ASTRONOMICKÝ KURZ
ELEKTŘINA A MAGNETIZMUS (MIT) •
MODULY •
STŘEDNÍ ŠKOLY
FYZIKA – RELATIVITA
|
|
Základní principy |
|
|
Některé experimenty |
|
|
Lorentzova transformace |
|
|
Základní vztahy |
|
|
Některé čtyřvektory |
|
|
Některé vztahy z OTR |
|
|
Některé důsledky OTR |
Základní principy
| Klasický princip relativity | Mechanické děje dopadnou ve
všech inerciálních soustavách stejně. Žádný z inerciálních
systémů není nijak privilegován. Tento princip vychází z Galileovy
transformace mezi dvěma souřadnicovými systémy vzájemně se pohybujícími
v ose x
konstantní rychlostí v:
t′ = t x′ = x − υt y′ = y z′ = z Derivováním podle času dostaneme klasické skládání rychlostí: ux′ = ux − υ uy′ = uy uz′ = uz Dalším derivováním zjistíme, že zrychlení v obou soustavách jsou stejná a = a′. To znamená, že v obou soustavách působí i stejné síly a platí klasický princip relativity. |
| Speciální relativita | 1. Mechanické i
elektromagnetické děje dopadnou ve všech inerciálních systémech stejně.
Žádný z inerciálních systémů není nijak privilegován.
2. Rychlost světla je ve všech inerciálních souřadnicových soustavách stejná. Princip konstantní rychlosti světla je obsažen v Maxwellových rovnicích a je podpořen celou řadou experimentů, z nichž nejznámější je Michelsonův experiment. Odpovídající transformace se nazývá Lorentzova transformace a nevede již k prostému skládání rychlostí. Délky tyčí a časové intervaly závisí na volbě souřadnicového systému. |
| Obecná relativita | 1. Všechny děje dopadnou v
libovolném souřadnicovém systému stejně. Žádný systém není nijak
privilegován.
2. Gravitaci a setrvačné děje od sebe nelze odlišit. V urychlující se raketě dochází ke stejným dějům jako ve skutečném gravitačním poli. Naopak ve volně padajícím letadle pociťujeme stav beztíže a gravitační pole nevnímáme. Bohužel jen na chvíli. Vyjádřením tohoto faktu je tzv. princip ekvivalence. |
| Princip ekvivalence | Setrvačná a gravitační hmotnost jsou si navzájem úměrné, při vhodné volbě jednotek jsou si rovné. Princip ekvivalence vede k neodlišitelnosti setrvačných a gravitačních jevů a umožňuje popisovat gravitaci za pomocí křivého časoprostoru. |
| Silný princip ekvivalence | Energie odpovídající elektromagnetickému poli se také projevuje jako setrvačná hmotnost. I tato hmotnost má své gravitační účinky. |
| Velmi silný princip ekvivalence | Energie, která by odpovídala samotnému gravitačnímu poli má také projevy jako setrvačná a gravitační hmotnost. |
| Matematický popis OTR | 1. Každé těleso zakřivuje svou
přítomností prostor a čas kolem sebe.
2. V tomto zakřiveném prostoročase se tělesa pohybují po nejrovnějších možných drahách (geodetikách). Tělesa tedy časoprostor sama vytvářejí, bez nich časoprostor neexistuje a nemá smysl. |
Některé experimenty |
|
| Michelsonův-Morleyův (1887) | Zjišťoval rozdíl v rychlosti šíření světla v pohyblivé soustavě ve dvou navzájem kolmých směrech. Výsledek tohoto i dalších experimentů (Kennedy-Thorndike, Rayleigh-Brace, Trouton-Noble) byl jednoznačný: Světlo se šíří za všech okolností stejnou rychlostí c. |
| Eötvösův (1889) | Ověření ekvivalence setrvačné a gravitační hmotnosti. Základem
experimentu byly dvě koule stejné hmotnosti, zavěšené ve vodorovné rovině na
torzním vlákně. Na rotující Zemi na koule působí kombinace gravitačních sil
(souvisí s gravitační hmotností) a odstředivých sil (souvisí se setrvačnou
hmotností). V případě, že by obě hmotnosti nebyly stejné by došlo ke zkroucení
vlákna vlivem nenulového momentu sil. Nic takového nebylo pozorováno. Relativní
přesnost Eötvösova experimentu byla 10−8. Pozdější experimenty
ověřily ekvivalenci setrvačné a gravitační hmotnosti s vyšší přesností
1909: Pekar, Feket; 10−9 |
| Waagův | Hledání inerciálního systému. Globální inerciální systém neexistuje. Zkonstruovat lze jen lokální inerciální systém. Tím je každá po krátkou dobu volně gravitující klec (například utržený výtah). Právě takovýto systém je inerciální a platí v něm zákony speciální relativity. Tedy tělesa se pohybují konstantními rychlostmi a po přímkách, světlo se pohybuje po přímce rychlostí c. V tomto inerciálním systému je gravitační pole odtransformováno volným pádem „klece“. Nejsou však odtransformovány vyšší derivace pole. Haroldův Waagův experiment dokazuje, že ve volně gravitující kleci se tělesa pohybují po přímkách. Popis tohoto experimentu naleznete na stránkách o Astrofyzice, v pasáži Gravitace v kapitole Obecná teorie relativity. |
| Poundův-Rebkův (1960) | V gravitačním poli dochází ke změně chodu času. Foton vystupující z gravitačního pole libovolného tělesa (Slunce, Země) mění svou frekvenci (odpovídá tikotu pomyslných hodin) a tím vlnovou délku, rudne. Naopak fotony vstupující do gravitačního pole těles modrají. Zmodrání fotonu na Zemi bylo pozorováno Pound a Rebkem při průletu starou vodárenskou věží vysokou 22.6 m v roce 1960. K detekci změny frekvence byl využit Mösbauerův jev. Zdrojem záření byly γ paprsky s energií 14.4 keV emitované izotopem kobaltu 57Co. Prohlédněte si příklad „Poundův-Rebkův experiment“. |
Lorentzova transformacePředpokládáme, že souřadnicový systém S ′ se pohybuje vzhledem k systému S rychlostí v ve směru osy x. Obě souřadnicové soustavy jsou inerciální. Význam relativistických koeficientů γ a β je definován v další tabulce. Při mnoha výpočtech je výhodné pracovat v takové soustavě jednotek, ve které je c = 1. Většina následujících vztahů se v této soustavě značně zjednoduší |
|
| t′ = γ (t
− υx/c2)
x′ = γ (x −υt) y′ = y z′ = z |
Lorentzova transformace S → S′. Transformace, která je ve shodě s Maxwellovými rovnicemi, nevychází z ní již prosté skládání rychlostí. Tato transformace splňuje oba základní Einsteinovy postuláty speciální relativity. |
| t = γ (t′
+ υx′/c2)
x = γ (x′ + υt′) y = y′ z = z′ |
Inverzní Lorentzova transformace S' → S. |
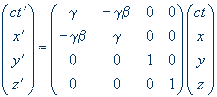 |
Lorentzova transformace S → S′ – maticový zápis. Transformace je dána jednoduchou Lorentzovou maticí Λ. Stejným způsobem se transformují i ostatní čtyřvektory - prostým působením Lorentzovy matice Λ. |
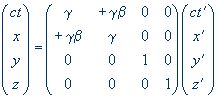 |
Inverzní Lorentzova transformace S → S′ – maticový zápis. Inverzní Lorentzova matice Λ−1 se od Lorentzovy matice Λ liší jen opačným znaménkem rychlosti pohybu druhé soustavy, tj. znaménkem koeficientu β. |
| det Λ = det Λ−1 = 1 | Unitarita transformace. Z matematického hlediska patří Loretzova transformace k unitárním transformacím. Ty lze rozdělit na rotace s determinantem rovným +1 a zrcadlení s determinantem rovným −1. LT tedy patří k rotacím. |
| u′ = (u − υ) / (1 − uυ/c2) | Transformace rychlosti S → S′. Rychlosti částice v obou soustavách jsou u = dx/dt, u′ = dx′/dt′, rychlost soustavy S′ vzhledem k S je υ. Transformační pravidlo získáme ihned diferencováním Lorentzových rovnic. Maximální rychlost z tohoto transformačního pravidla vychází c. |
| u = (u′ + υ) / (1 + u′υ/c2) | Transformace rychlosti S′ → S. Rychlosti částice v obou soustavách jsou u, u′, rychlost soustavy S′ vzhledem k S je υ. Maximální rychlost z tohoto transformačního pravidla vychází c. |
Základní vztahy |
|
| β ≡ υ/c | První relativistický koeficient. Bezrozměrná rychlost. |
| γ ≡ (1 − β2)−1/2 | Druhý relativistický koeficient. Lorentzův kontrakční faktor. |
| dt = γ dt0 | Dilatace času. Časový interval mezi dvěma událostmi (například počátkem a koncem shlédnutí filmu) je nejkratší ve vlastní soustavě (v soustavě spojené s oběma událostmi, tedy v kině). Všude jinde se zdá, že doba uběhlá mezi počátkem a koncem tohoto děje je delší. Prohlédněte si příklad „Mion“. |
| dl = dl0/γ | Kontrakce délek. Délka tyče (prostorový interval) je ve vlastní soustavě nejdelší možná. V každé jiné soustavě se tyče jeví kratší ve směru pohybu. Prohlédněte si příklad „Mion“ |
| m = γ m0 | Transformace hmotnosti. Hmotnost částice s narůstající rychlostí roste. V limitě υ → c roste nade všechny meze. Proto není možné žádnou částici s m0 ≠ 0 urychlit na rychlost světla. Rychlost světla je nejvyšší dosažitelná rychlost. Mají ji jen částice s m0 = 0 a to v libovolném souřadnicovém systému. |
| E = mc2 | Vztah mezi celkovou energií a hmotností. Jakékoli zvýšení energetického obsahu systému vede i k zvýšení jeho hmotnosti. Celková obsažená energie je právě dána hmotností systému. Prohlédněte si příklad „Slunce“. |
| p = mv | Celková hybnost částice. V obou posledních vztazích je m = γm0, tj. jde o pohybovou hmotnost. |
| Wk = mc2 − m0c2 | Kinetická energie. Taylorův rozvoj hodnoty m = γm0 v rychlosti do druhého řádu vede na klasický vztah Wk = mυ2/2. Prohlédněte si příklady „Parametry rychlé částice“. |
| E2 = p2c2 + m02c4 | Pythagorova věta o energii. Jde o užitečné vyjádření kvadrátu velikosti čtyřvektoru hybnosti. Pro nehmotné částice se redukuje na známý vztah E = pc, který platí například pro fotony. Pro malé hybnosti dá výraz klasický vztah E = E0 + p2/2m pro hmotné částice. |
Některé čtyřvektory |
|
| xμ = (ct, x) | Událost. Základní čtveřice parametrů popisujících v relativitě událost. Koeficient c v časové komponentě zajišťuje stejný rozměr všech čtyř veličin. V soustavě jednotek c = 1 tento koeficient odpadá a mocniny c nebudou ani u následujících výrazů. |
| kμ = (ω/c, k) | Vlnový čtyřvektor. Popisuje vlnění a změny jeho fáze. Časová složka ω je změna fáze vlnění s časem, prostorové složky k jsou změny fáze s jednotlivými souřadnicemi. Prohlédněte si příklad „Dopplerův jev“. |
| pμ = (E/c, p) | Čtyřhybnost. Popisuje částice. Časová složka E je energie, souvisí se symetriemi v přírodě vzhledem k časovým posunutím. Prostorová složka p je hybnost, souvisí se symetriemi v přírodě vzhledem k prostorovým posunutím. V kvantové teorii se objekty mohou chovat jako vlny i jako částice. Vyjádřením této duality vlna-částice je vztah pμ ~ kμ . Konstantou úměrnosti je v SI redukovaná Planckova konstanta. |
| Aμ = (ϕ/c, A) | Čtyřpotenciál elektromagnetického pole. Elektrická a magnetická pole se určí z výrazů E = − ∇ϕ − ∂A/∂t, B = rot A. Prohlédněte si příklad „Heavisideovo pole“. Prohlédněte si aplet „Heavisideovo pole“. |
| jμ = (cρ, j ) | Čtyřproud. Hustota náboje a proudová hustota. Čtyřproud popisuje proudění nějaké veličiny, v tomto případě elektromagnetického náboje. Stejně tak můžeme přiřadit čtyřproud i jiným aditivním veličinám, například energii: Potom je ρ = E·D/2 + H·B/2 hustota energie elektrického a magnetického pole a j = E×H je tok energie, tzv. Poyntingův vektor. |
| uμ = dxμ/dτ = (γc, γv) | Čtyřrychlost. Rychlost je definována pomocí derivace podle vlastního času, který je invariantem vzhledem k LT. Tím je zaručeno, že i čtyřrychlost se chová jako čtyřvektor a má stejné transformační vlastnosti jako ostatní čtyřvektory. |
| pμ = m0 uμ | Čtyřhybnost. Definice pomocí čtyřrychlosti. Musíme ji násobit klidovou hmotností, která je invariantem vzhledem k LT,. Tím je zaručeno, že i čtyřhybnost má stejné transformační vlastnosti jako ostatní čtyřvektory. Porovnáme-li vyjádření z třetího řádku s tímto, získáme vztahy E = mc2 a p = mv, ve kterých je m = γm0. |
| Všechny čtyřvektory se transformují shodně - za pomoci Lorentzovy transformace. Stačí zapůsobit na čtyřvektor vyjádřený v jedné soustavě Lorentzovou maticí a získáme hodnoty v soustavě druhé (obě soustavy musí být inerciální). Skalární součin dvou čtyřvektorů definovaný vztahem aμbμ = − a0b0 + a1b1 + a2b2 + a3b3 je invariantem a nezávisí na volbě souřadnicového systému. Například xμkμ = − ωt + k·x je fáze vlnění, dxμdxμ = − c2dt2 + dx2 + dy2 + dz2 je takzvaný interval (prohlédněte si příklad „Interval“), jμ Aμ = j·A − ρϕ popisuje interakci toku nabitých částic s polem atd. | |
Některé vztahy z OTR |
|
| Δω/ω0 = − Δλ/λ0 = Δϕ/c2 | Změna frekvence fotonu způsobená změnou gravitačního potenciálu ϕ. V tíhovém poli je Δϕ = gΔl. Prohlédněte si příklady „Poundův-Rebkův experiment“. |
| rg = 2GM/c2 | Schwarzschildův poloměr. Poloměr, pod ze kterého se od hmotného tělesa nemůže vzdálit ani světlo. |
| ds2 = − c2(1 − rg/r)dt2
+ (1 − rg/r)−1dr2 + r2dθ2 + r2 sin2θ dφ2 |
Schwarzschildova metrika. Tvar intervalu ve sférických souřadnicích v okolí černé díry. |
| M, L, Q = const | „No hair“ teorém. Černá díra si ponechává jen informaci o hmotnosti, momentu hybnosti a náboji. |
| ΣSk(t) ≤ ΣSk(t+Δt) | Termodynamika černých děr. Ať probíhají jakékoli procesy včetně spojování černých děr, celkový povrch se nezmenší. Povrch černé díry v jistém smyslu představuje pojem entropie klasického souboru částic. |
| H ≡ V/R; V= dR/dt | Hubbleova konstanta. Udává koeficient úměrnosti mezi rychlostí rozpínámí vesmíru a vzdáleností objektu. H ~ 50 km s−1Mpc−1. |
| 8/3 πρG − (V/R)2 = k | Einsteinova rovnice. Rovnice pro expanzní funkci R(t). Veličina k je křivost vesmíru. |
| ρc = 3H2/(8πG) | Kritická hustota. Pro hustotu vyšší než je kritická se Vesmír bude v budoucnu smršťovat, jeho křivost je kladná a objem konečný. Pro hustotu nižší než kritická je křivost záporná, objem nekonečný a vesmír se bude neustále rozpínat. |
| z = Δλ/λ0 = [R(t) − R(t0)]/R(t0) | Kosmologický posuv. Změna frekvence vyzařovaného světla způsobená změnou geometrie prostředí, kterým se světlo šíří, tedy rozpínáním Vesmíru. Prohlédněte si příklad „Kosmologický posuv“. |
Některé důsledky OTR
|
|
| Termo | Kmity | Vlny | Elmg | Optika | Relativita | Kvanta |
| Příklady | Příklady | Příklady | Příklady | Příklady | Příklady | Příklady |
