FYZIKA I • FYZIKA II • FYZIKA • TEORETICKÁ MECHANIKA (TF1) • KVANTOVÁ TEORIE (TF2)
STATISTICKÁ FYZIKA (TF3) • VZTAH MATEMATIKY A FYZIKY (TF4) • OBECNÁ RELATIVITA (TF4)
ELEKTROMAGNETICKÉ POLE (TF4) • FYZIKA PLAZMATU • ASTROFYZIKA • ASTRONOMICKÝ KURZ
ELEKTŘINA A MAGNETIZMUS (MIT) • MODULY • STŘEDNÍ ŠKOLY

FYZIKA – KVANTOVÁ TEORIE (PŘÍKLADY)

	Stefanův-Boltzmannův zákon
	Wiennův zákon
	Slunce
	Člověk
	Čára Hα
	Mikroskop
	Komutátor
	Jáma
	Emise

Příklad 1: Stefanův-Boltzmannův zákon

Zadání: Nalezněte z Planckova vyzařovacího zákona závislost celkové intenzity záření na teplotě.

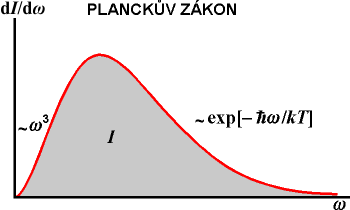
Řešení: Stačí integrovat Planckovu formuli přes všechny frekvence a úhly. Do konstanty „const“ zahrnujeme číselné koeficienty. Mezi ně patří nakonec i bezrozměrný integrál v posledním řádku, jehož hodnotu by bylo možné určit numericky:

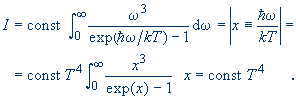
Příklad 2: Wiennův zákon

Zadání: Nalezněte z Planckova vyzařovacího zákona závislost vlnové délky maxima vyzařování na teplotě.

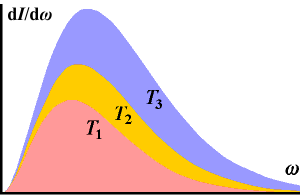
Řešení: K hledání maxima využijeme Planckův zákon ve frekvencích, který je jednodušší pro derivování. Nutná podmínka maxima je

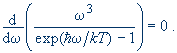
Po derivování a jednoduchých úpravách podmínka přejde na rovnici

(3 − ħω/k_BT)exp(ħω/k_BT) = 3,

ve které označíme

x = ħω/k_BT

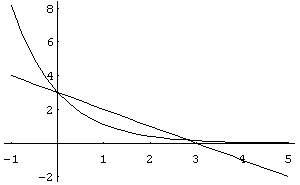
a získáme transcendentní rovnici (3 − x) = 3 exp(−x). Tato rovnice může být snadno řešena numericky nebo graficky (v grafu najdeme průsečík funkcí na levé a pravé straně rovnice). Řešení rovnice je buď x = 0 (toto řešení je triviální a vede na nulovou frekvenci) nebo x ~ 2.82144 (hledané řešení). Z definice x je zřejmé, že ω_max ~ T, neboli λ_max ~ 1/T.

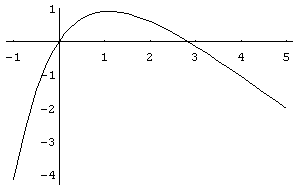Graf křivky 3 − x a křivky 3 exp(−x)	Graf křivky 3 − x − 3 exp(−x)

Příklad 3: Slunce

Zadání: Nalezněte povrchovou teplotu Slunce, víte-li, že u Země je intenzita záření I_Z = 1.4 kW/m². Nalezněte povrchovou teplotu Slunce také z faktu, že maximum vyzařování je ve žluté barvě s λ_max = 500 nm.

Další údaje: Vzdálenost Země od Slunce R_ZS = 150×10⁶ km, poloměr Slunce R_S = 700 000 km.

Řešení: Známe-li intenzitu záření Slunce u naší Země, můžeme určit celkový výkon Slunce P = 4πR_ZS²I_Z. Z celkového výkonu spočteme intenzitu vyzařování na povrchu Slunce I_S = P/4πR_S². Ta je podle Stefanova-Boltzmannova zákona rovna σT⁴. Pro teplotu na povrchu tak vychází:

T = [I_ZR_ZS²/σR_S²]^1/4.

Z Wiennova posunovacího zákona víme, že vlnová délka maxima vyzařování je  λ_max = b/T, odsud snadno určíme teplotu povrchu Slunce:

T = b/λ_max .

Výsledek: Oběma postupy vychází teplota povrchu Slunce cca 5 800 K.

Příklad 4: Člověk

Zadání: Nalezněte vlnovou délku na které vyzařuje maximum energie člověk o teplotě 37 °C.

Předpoklady: Člověk září jako absolutně černé těleso.

Řešení: Využijeme Wiennův posunovací zákon λ_max = b/T = 0.00289/310 m = 9.3×10⁻⁶ m. Maximum je v infračervené oblasti. Na této vlnové délce musí být citlivá různá čidla monitorující pohyb člověka (bezpečnostní systémy apod.).

Příklad 5: Čára H_α

Zadání: Nalezněte vlnovou délku vodíkové čáry H_α (přechod z hladiny n = 3 na hladinu n = 2).

Řešení: Při přechodu se uvolní energie ΔE = E₃ − E₂ = E₁/9 − E₁/4 = −13,6 eV (1/9 − 1/4) = 1.88 eV. Tato energie je rovna energii vyzářeného fotonu ΔE = ħω = ħ 2πc/λ. Odsud již snadno určíme vlnovou délku.

Výsledek: λ = 656 nm.

Příklad 6: Mikroskop

Zadání: Nalezněte maximální možnou (teoretickou) rozlišovací schopnost elektronového mikroskopu. Elektrony jsou urychleny potenciálovým rozdílem 10⁴ V.

Řešení: Elektron v elektronovém mikroskopu se chová jako vlna, mezní rozlišovací schopností je sama vlnová délka elektronu. Od částicových vlastností je tedy třeba přejít k vlnovým vlastnostem elektronu. Elektron je urychlen na kinetickou energii m_eυ²/2 = QU. Z této rovnice zjistíme rychlost částice. Vzhledem k malému urychlujícímu napětí jsme použili jen nerelativistický vztah. Pro vyšší napětí by bylo třeba rychlost najít z relativistického vztahu (prohlédněte si příklad „Parametry rychlé částice“). Nyní přejdeme k vlnovým vlastnostem podle Heisenbergova vztahu p = ħk. Vzhledem k nerelativistické situaci je v převodní rovnici  p = m_eυ a k = 2π/λ.

Výsledek: Mezní rozlišovací schopnost je rovna vlnové délce elektronu λ = h (2m_eQU)^−1/2 ~ 10⁻¹¹ m.

Příklad 7: Komutátor

Zadání: Nalezněte komutační relaci mezi operátorem násobení souřadnicí a operátorem derivování.

Řešení: Přímo z definice komutátoru nalezneme výsledek:

[x, d/dx] f = (x d/dx − d/dx x) f = x df/dx − d/dx (xf ) = x df/dx − f − x df/dx = − f .

Porovnáme-li první a poslední výraz, zjistíme:

[x, d/dx] = −1.

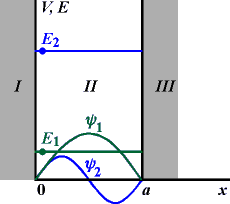
Příklad 8: Jáma

Zadání: Nalezněte energetické hladiny v potenciálu nekonečné pravoúhlé jámy

.

Řešení: V oblastech I a III je jediné řešením bezčasové Schrödingerovy rovnice ψ = 0 (potenciál je nekonečný). Z fyzikálního hlediska to znamená, že pravděpodobnost výskytu částice je nulová. Kdyby byla jáma konečná (konečný potenciál vně jámy), byla by vlnová funkce ψ v těsné blízkosti hranice jámy nenulová. Částice by měla sice malou, ale nenulovou pravděpodobnost existence i za hranicí jámy. V oblasti II má Schrödingerova rovnice tvar

který lze upravit na standardní rovnici kmitů

s jednoduchým řešením

ψ = A sin kx + B cos kx.

Vlnová funkce musí být spojitá na obou hranicích jámy, proto musí platit ψ(0) = 0, ψ(a) = 0. Řešením této okrajové podmínky je

B = 0 , k = πn/a ,     n = 1, 2, 3, ... .

Podmínka pro k není nic jiného než energetické spektrum (energie vystupuje v definici k).

Výsledek:

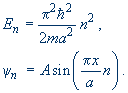
Prohlédněte si aplet „Jáma“.

Příklad 9: Emise

Zadání: Určete relativní nepřesnost ve vlnové délce fotonu vyzářeného atomem při přeskoku elektronu mezi dvěma hladinami. Předpokládejte, že emisní akt trvá 10⁻⁸ s. Konkrétní výpočet proveďte pro λ = 500 nm.

Řešení: Vyjdeme z limitního případu Heisenbergových relací neurčitosti:

ΔEΔt ~ ħ/2,  ħΔωΔt ~ ħ/2, Δ(2πc/λ) Δt ~ 1/2,  (2πc/λ2) Δλ Δt ~ 1/2,  Δλ /λ ~ λ/(4πcΔt).

Výsledek: Relativní přesnost vyzářené vlnové délky fotonu je Δλ/λ ~ 1.4×10⁻⁸.

Termo	Kmity	Vlny	Elmg	Optika	Relativita	Kvanta
Příklady	Příklady	Příklady	Příklady	Příklady	Příklady	Příklady