FYZIKA I • FYZIKA II • FYZIKA • TEORETICKÁ MECHANIKA (TF1) • KVANTOVÁ TEORIE (TF2)
STATISTICKÁ FYZIKA (TF3) • VZTAH MATEMATIKY A FYZIKY (TF4) • OBECNÁ RELATIVITA (TF4)
ELEKTROMAGNETICKÉ POLE (TF4) • FYZIKA PLAZMATU • ASTROFYZIKA • ASTRONOMICKÝ KURZ
ELEKTŘINA A MAGNETIZMUS (MIT) • MODULY • STŘEDNÍ ŠKOLY

FYZIKA – KMITY (PŘÍKLADY)

	Zkumavka
	Tunel v Zemi
	Morseův potenciál
	Oběh Země kolem Slunce
	Tlumení v energii
	Amplitudová a výkonová rezonance
	Fázový portrét oscilátoru
	Numerické schéma
	Skládání kmitů, vlastní frekvence

Příklad 1: Zkumavka

Zadání: Zkumavka zatížená broky se pohupuje na vodní hladině. Určete frekvenci a periodu kmitů. Průřez zkumavky je S = 1 cm² a hmotnost zkumavky s broky m = 20 g.

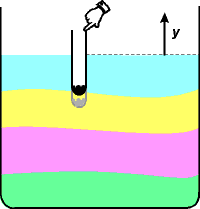
Předpoklady: Kmity zkumavky neovlivní výšku hladiny vody v kádince.

Řešení: Nekmitá li zkumavka, je v rovnováze vztlaková síla s tíhovou. Porušíme-li rovnováhu, objeví se vratná vztlaková síla (hydrostatický vztlak) a kmity zkumavky můžeme popsat pohybovou rovnicí:

m d²y/dt² = pS = −ρgyS.

Tuto rovnici uvedeme na standardní tvar d²y/dt² + (ρgS/m) y = 0 a zjistíme úhlovou frekvenci kmitů ω = (ρgS/m)^1/2. Periodu již snadno určíme ze vztahu T = 2π/ω.

Výsledek: ω = 7 s⁻¹, T = 0.9 s.

Příklad 2: Tunel v Zemi

Zadání: Představte si, že napříč Zemí je vystavěn tunel, do kterého vhodíme nějaký předmět. Jaký pohyb bude vykonávat? Vrátí se někdy zpět? Jestliže ano, kdy?

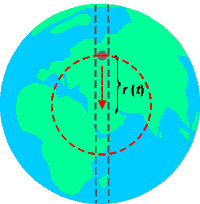
Předpoklady: Zemi půjde provrtat a vnitřní teplo a tlak tunel nezničí. Těleso se při průletu neroztaví. Hustota Země je konstantní. Poloměr Země je R = 6 400 km a hmotnost M = 6×10²⁴ kg.

Řešení: Na předmět o hmotnosti m₀ působí gravitačně jen část Země uvnitř poloměru r(t), která má hmotnost m(r) = M r³/R³ (v poměru objemů). Pohybová rovnice potom je

m₀d²r/dt² = − Gm₀m(r)/r² = −(Gm₀M/R³) r.

Jedná se o rovnici kmitů, kterou upravíme na standardní tvar d²r/dt² + (GM/R³) r = 0 a odečteme úhlovou frekvenci kmitů ω = (GM/R³)^1/2. Periodu určíme opět ze vztahu T = 2π/ω.

Výsledek: Předmět se vrátí za 1.4 hodiny.

Příklad 3: Morseův potenciál

Zadání: Dvojatomová molekula má potenciální energii danou potenciálem W_p(r) = W₀(1 − exp [−α(r−r₀)²]). Nakreslete průběh potenciální energie, diskutujte oblast přitažlivých a odpudivých sil. Nalezněte úhlovou frekvenci oscilací.

Předpoklady: Rozkmity jsou malé, potenciální energii jde nahradit parabolickou závislostí.

Průběh potenciální energie:

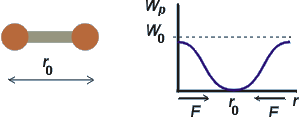
Řešení: Jde o průběh potenciální energie s minimem v r₀ (viz obrázek). Pro r < r₀ je síla odpudivá a pro r > r₀ je síla přitažlivá (míří vždy k minimu potenciální energie). Výsledným pohybem proto budou kmity. Potenciál nahradíme pomocí Taylorova rozvoje parabolickou závislostí:

.

Jde o harmonický oscilátor (parabolická závislost energie na výchylce z minima). Označíme-li tuhost oscilátoru k ≡ W_p″(r₀) = 2αW₀ a výchylku z rovnovážné polohy y ≡ r − r₀ máme

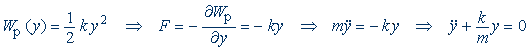
a standardním způsobem určíme frekvenci

.

Příklad 4: Oběh Země kolem Slunce

Zadání: Země obíhá kolem Slunce po elipse s malou excentricitou. Vzdálenost od Slunce proto periodicky kolísá. Určete frekvenci a periodu těchto oscilací.

Předpoklady: Pohyb je rovinný, celkový moment hybnosti b = 2.7×10⁴⁰ kgm²s⁻¹.

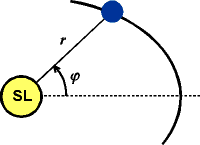
Řešení: Při pohybu se zachovává celková energie a celkový moment hybnosti Země:

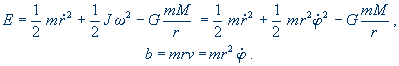
První člen v energii souvisí s radiálním pohybem Země (přibližování ke Slunci a a vzdalování od Slunce). Druhý člen odpovídá kinetické energii rotace Země kolem Slunce a třetí člen gravitační potenciální energii. Oběžná rychlost je označena v. K popisu pohybu využíváme polární souřadnice. Při pohybu se radiální i úhlová proměnná mění s časem. Výše uvedené kombinace jsou ale v průběhu celého pohybu neproměnné. Zajímá nás pohyb v radiální souřadnici, proto z druhé rovnice vyloučíme časovou derivaci úhlu a dosadíme do první rovnice. Pro zákon zachování energie tak dostaneme

Část energie závisící na poloze r můžeme chápat jako efektivní potenciální energii, která se skládá z potenciální energie odstředivých sil (~1/r²) a gravitační potenciální energie (~ − 1/r):

Tato potenciální energie má minimum. Standardním postupem (viz minulý příklad) určíme pozici minima energie r₀ (střední vzdálenost Země od Slunce), „tuhost“ oscilátoru k ≡ W″_{p, ef}(r₀), frekvenci a periodu kmitů.

Výsledek: r₀ ~ 150×10⁶ km, T ~ 365 dní.

Příklad 5: Tlumení v energii

Zadání: Amplituda tlumeného kmitu klesá s časem podle vztahu A(t) = A₀ e^−δt. Určete jakým způsobem klesá energie.

Řešení: Podle definice má harmonický oscilátor kvadratickou závislost energie na výchylce (například potenciální energie W_p = 1/2 ky², celková energie E = 1/2 kA²). Energie bude tedy ubývat podle výrazu E(t) = E₀ e^−2δt.

Příklad 6: Amplitudová a výkonová rezonance

Zadání: Nalezněte maximum amplitudy a maximum přeneseného výkonu u vynucených kmitů.

Předpoklady:Označíme ω₀ vlastní frekvenci oscilací, Ω frekvenci vnější síly a δ koeficient útlumu. Známe velikost amplitudy vynucených kmitů a velikost průměrného přeneseného výkonu:

|A| ~ 1/[(Ω² − ω₀²)² + 4δ²Ω²]^1/2;    P/P_max ~ 4δ²Ω²/[(Ω² − ω₀²)² + 4δ²Ω²].

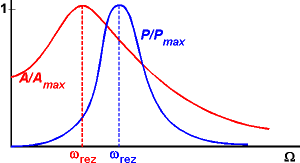
Řešení: Je třeba nalézt maximum obou výše uvedených funkcí vzhledem k vynucující frekvenci Ω. Není nutné začít tyto funkce bezhlavě derivovat. Stačí si uvědomit, že má-li například první funkce maximum, bude ho také mít argument v odmocnině. Má-li tento argument maximum, bude mít jmenovatel v odmocnině minimum. Stačí tedy derivovat jen jmenovatel uvedené funkce a výsledek položit rovný nule. Obdobně u druhé funkce není nutné řešit celou podmínku pro podíl (u' v − uv' )/v² = 0, ale jen podmínku u' v = uv' . Dokonce nemusíme derivovat podle Ω, ale postačí derivovat jen podle Ω². Pro maximum amplitudy tak dostaneme podmínku

2(Ω² − ω₀²)+ 4δ² = 0,

ze které plyne rezonanční frekvence

Ω_rez = [ω₀² − 2δ²]^1/2.

Pro maximum přeneseného výkonu získáme po derivování vztah

4δ² [(Ω² − ω₀²)²+ 4δ²Ω²] = 4δ²Ω²[2(Ω² − ω₀²)+ 4δ²],

který po vykrácení a odečtení stejných členů přejde na

(Ω² − ω₀²)²= 2Ω²(Ω² − ω₀²).

Pozor! Dalším zkrácením výrazů na obou stranách bychom přišli o hledané řešení:

Ω_rez = ω₀

Výsledek: Amplituda je nejvyšší při frekvenci Ω_rez = [ω₀²− 2δ²]^1/2, přenesený výkon je nejvyšší při frekvenci Ω_rez = ω₀.

Příklad 7: Fázový portrét oscilátoru

Zadání: Nalezněte fázový portrét (závislost výchylky na rychlosti nebo hybnosti) pro harmonický oscilátor.

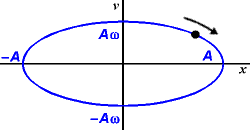
Řešení: Oscilátor koná harmonické kmity dle vztahu x(t) = A cos(ωt). Rychlost je dána první derivací: v(t) = −Aω sin(ωt). Z těchto dvou vztahů vyloučíme čas. Stačí například ze vztahů vypočíst funkce sinus a kosinus, umocnit na druhou a sečíst.

Výsledek: Výsledkem je rovnice elipsy ve tvaru: (x/A)² + (v/Aω)² = 1. Můžete si představit, že po fázové trajektorii se pohybuje kulička, pohyb v ose x a v jsou odpovídají projekcím pohybu kuličky do těchto os. Fázový portrét bývá velmi důležitou charakteristikou popisovaného systému. Ne vždy je takto jednoduchý. U složitějších systémů můžeme z fázového portrétu určit oblasti, ve kterých systém osciluje, oblasti, ve kterých je stabilní nebo nestabilní. Různé oblasti fázového portrétu jsou odděleny křivkami, které nazýváme separatrisy.

Příklad 8: Numerické schéma

Zadání: Navrhněte jednoduché diferenční schéma pro kyvadlo s velkými výchylkami.

Předpoklady: Zanedbejte hmotnost závěsu kyvadla.

Řešení: Vyjdeme ze standardní pohybové rovnice pro rotační pohyb Jd²φ/dt² = M_F . Za moment setrvačnosti dosadíme J = ml² a za moment síly M_F = − mgl sin φ. Získáme tak výchozí diferenciální rovnici

která by pro malé rozkmity přešla v standardní rovnici harmonických oscilací, kterou umíte řešit. Pro obecné rozkmity ji musíme řešit numericky. Převedeme ji na soustavu dvou rovnic prvního řádu:

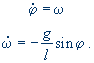
Časové derivace v rovnicích nahradíme konečnými přírůstky:

.

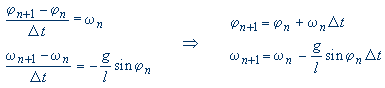
Získáme tak schéma (předpis), ze kterého z počátečních podmínek φ₀ a ω₀ vypočteme hodnoty φ₁ a ω₁ v čase o Δt pozdějším, z těchto hodnot hodnoty φ₂ a ω₂, atd. Řešení je tak diskretizováno s časovým krokem Δt. Existují samozřejmě přesnější numerická schémata, ale základní princip snad na tomto příkladu pochopíte.

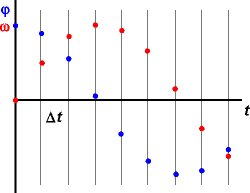
Příklad 9: Skládání kmitů, vlastní frekvence

Zadání: Dvě kyvadla jsou spojena napříč pružinou s malou tuhostí k. Nalezněte vlastní frekvence a vlastní kmity systému. Jak bude vypadat obecný kmit soustavy?

Předpoklady: Každé z kyvadel by samo o sobě kývalo harmonicky s frekvencí ω₀.

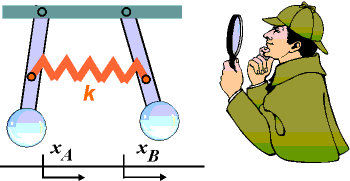
Řešení: Základní rovnice pro pohyb obou kyvadel budou doplněny o další harmonickou sílu odpovídající pružině:

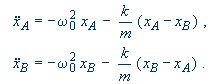
Vlastním kmitem rozumíme takový kmit systému, při kterém všechny části systému kmitají (zde kývají) se stejnou frekvencí. Do soustavy proto dosadíme hledané řešení x_A = A exp[iωt],  x_B = B exp[iωt]. Získáme tak algebraickou soustavu rovnic pro amplitudy A a B

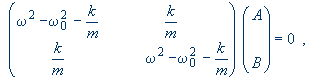
která má dvě nenulová řešení (determinant matice soustavy musí být nulový):

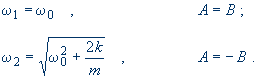
Výsledek: Soustava má dvě vlastní frekvence a dva vlastní kmity. První vlastní kmit odpovídá synchronnímu pohybu obou kyvadel (A = B) a má původní frekvenci kyvadel. Frekvence tohoto modu tedy není ovlivněna pružinou.

Druhý vlastní kmit odpovídá pohybu kyvadel proti sobě (A = − B). Soustava koná kyvy na frekvenci ω₁ poněkud vyšší než ω₀ (pružina přispívá k tuhosti systému).

Libovolný jiný kyv systému je z důvodu linearity superpozicí předchozích řešení. Typické je vychýlení jednoho kyvadla, které začne předávat energii druhému kyvadlu a postupně se utlumí. Potom bude druhé kyvadlo předávat energii zpět prvnímu, atd. Můžeme hovořit buď o předávání energie a o rezonanci nebo o superpozici dvou vlastních kmitů s blízkou frekvencí, která vede na rázy.

Termo	Kmity	Vlny	Elmg	Optika	Relativita	Kvanta
Příklady	Příklady	Příklady	Příklady	Příklady	Příklady	Příklady