
Gravitace | Různé metriky
Kartézské souřadnice
Metrika vlastně popisuje vzdálenost dvou bodů v prostoru nebo v časoprostoru. Nahrazuje nám tak Pythagorovu větu pro infinitezimálně malý úsek vzdáleností a umožňuje vypočítat mnohé vlastnosti prostoru či časoprostoru. Jednoduché příklady naleznete ve skriptu Astrofyzika v příkladech, komplexnější pohled ve skriptu věnovaném Obecné relativitě. K druhému z nich existují i kompletní nahrávky přednášek. Používáme-li k popisu známého prostoru jen nový typ ortogonálních souřadnic (souřadnicové plochy jsou navzájem kolmé), stačí se infinitezimálně z daného bodu posunout ve směru jednotlivých souřadnicových os a sečíst kvadráty těchto posunutí. Jde vlastně o aplikaci Pythagorovy věty. V obecně zakřiveném časoprostoru je třeba metriku vypočítat z Einsteinových rovnic OTR. Často jsou k dispozici nekorektní a nepřesné postupy, které však mohou jednoduchým způsobem ukázat alespoň tvar metriky v dané situaci. V kartézských souřadnicích (x, y, z) jsou infinitezimální posuny ve směru jednotlivých os, interval a metrické koeficienty dány vztahy
dlx = dx, dly = dy, dlz = dz,
dl2 = dx2 + dy2 + dz2,
gij = diag {1,1,1}.
Polární souřadnice
V polárních souřadnicích (r,φ) je situace obdobná. Jen je třeba si uvědomit, že posuneme-li se v úhlu φ, pohybujeme se po infinitezimálním oblouku, který je dán jako součin poloměru a úhlu. Metrické koeficienty již nejsou rovny jedné. Tentokrát je prostor rovný, křivočaré jsou jen použité souřadnice
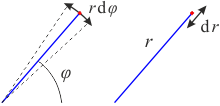
dlr = dr, dlφ = r dφ,
dl2 = dr2 + r2dφ2,
gij = diag {1, r2}.
Sférické souřadnice
Ve sférických souřadnicích (r, θ, φ) je posun v radiální souřadnici evidentně dr. Posouváme-li se v úhlu θ (rozevíráme kuželovou plochu), je posun roven oblouku r dθ. Posun v úhlu φ znamená pootočení plochy konstantního φ. Bod se posune o r⊥dφ = r sin θ dφ. Proto máme (nezajímají-li nás podrobnosti o úhlových částech metriky, zkracujeme je symbolem dΩ2. ):
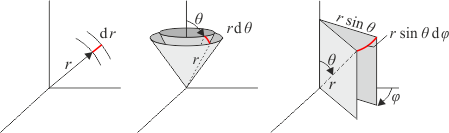
dlr = dr, dlφ = rdθ, dlφ = r sin θ dφ,
dl2 = dr2 + r2dθ2 + r2 sin2θ dφ2 ≡ dr2 + r2 dω2,
gij = diag {1, r2, r2 sin2θ}.
Souřadnice na povrchu koule
Představme si, že chceme vybudovat souřadnicový systém na povrchu kulové plochy o poloměru R. Použijeme nejprve standardní 3D kartézské souřadnice vycházející ze středu koule. Předpokládejme, že osa z protíná povrch koule v místě pozorovatele, a vytváří tak na povrchu koule přirozený pól. Souřadnice x a y lze v těsné blízkosti pólu (pozorovatele) považovat za lokální kartézský systém na povrchu koule. Dále od pólu je ale zjevné, že průsečíky souřadnicových rovin s povrchem koule nejsou přímky.
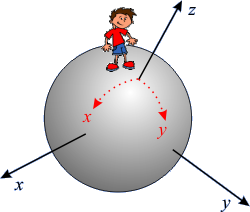
Integrální a diferenciální vztahy pro povrch koule (množinu bodů vzdálených od zvoleního středu R) dávají
x2 + y2 + z2 = R2; xdx + ydy + zdz = 0.
V elementu vzdálenosti budeme pomocí uvedených vztahů postupně eliminovat poslední proměnnou z:
dl2 = dx2 + dy2 + dz2 = dx2 + dy2 + (xdx + ydy)2/(R2 − x2 − y2).
Zavedeme-li běžným způsobem polární souřadnice (v těsné blízkosti pólu se tyto souřadnice budou pozorovateli zdát jako lokální polární souřadnice na povrchu koule, souřadnice r má význam vzdálenosti od osy z)
x = r cos φ; y = r sin φ,
dostaneme po dosazení a úpravách metriku s modifikovaným radiálním členem
dl2 = dr2/(1 – r2/R2) + r2dφ2.
Často se zavádí takzvaná skalární (Gaussova) křivost k ≡ 1/R2. S tímto označením získá metrika finální tvar:
dlr = dr/(1 − k r2)1/2, dlφ = r dφ,
dl2 = dr2/(1 − k r2) + r2dφ2,
gij = diag {1/(1 − k r2), r2}.
Poprvé v tomto příkladu znamenají nejednotkové koeficienty u metriky skutečně zakřivený „svět“. Budeme-li na povrchu koule konstruovat kružnice, nebude jejich obvod roven 2πa, kde a je poloměr měřený po povrchu koule. Stejný příklad řešený pro 3D „povrch“ na 4D kouli naleznete ve skriptu Astrofyzika v příkladech.
Minkowského metrika ve speciální relativitě
Jedním ze základních postulátů speciální teorie relativity je experimentálně mnohokrát ověření tvrzení, že světlo se ve všech soustavách šíří se stejnou rychlostí. Míjejí-li se dvě souřadnicové soustavy a bliknu-li baterkou v počátku soustav právě když jsou počátky na stejném místě, bude se světlo v obou soustavách šířit v kulových vlnoplochách z počátku: dl2 = c2dt2, dl' 2 = c2dt' 2. V obou soustavách tedy platí dx2 + dy2 + dz2 = c2dt2, neboli −c2 dt2+ dx2 + dy2 + dz2 = 0. Právě kombinace na levé straně je vždy ve všech souřadnicových soustavách stejná a nazývá se interval. Přejímá význam vzdálenosti, resp. kvadrátu velikosti vektoru ve čtyřrozměrném časoprostoru. Čas budeme klást na nulté místo v pořadí souřadnic (časoprostor). Bylo by možné ho také klást na čtvrté pořadí (prostoročas). Minkowského metriku lze zapsat jak v kartézských, tak ve sférických souřadnicích. I ve sférických souřadnicích jde stále o zápis metriky plochého časoprostoru:
| Kartézské souřadnice |
|---|
ds2 = −c2 dt2+ dx2 + dy2 + dz2, gij = diag {−c2 , 1, 1, 1}. |
| Sférické souřadnice |
ds2 = −c2 dt2 + dr2 + r2dθ2 + r2 sin2θ dφ2, gij = diag {−c2, 1, r2, r2 sin2θ}. |
Schwarzschildova metrika
Schwarzschildovo řešení je řešení Einsteinových rovnic v okolí sféricky symetrického hmotného objektu. Souřadnicový systém S zvolíme nepohyblivý vzhledem k objektu, systém je zjevně neinerciální. Představme si další systém LIS, tentokrát inerciální, který padá z nekonečna k uvažovanému objektu. Jeho okamžitá rychlost je ve vzdálenosti r od objektu rovna v = (2Gm/r)1/2. Rychlost měříme vzhledem k objektu. V padajícím LIS zjistíme kontrakci délek a dilataci času událostí v S:
dr = drLIS/γ; dt = γdtLIS,
koeficient γ je dán rychlostí pohybu
γ = (1 − v2/c2)−1/2 = (1 − 2GM/rc2)−1/2 = (1 − rg/r)−1/2,
kde jsme označili tzv. Schwarzschildův poloměr
rg ≡ 2GM/c2.
V LIS platí speciální relativita a lze použít Minkowského metriku
ds2 = − c2 dt2LIS + dr2LIS.
Metrika v pevném souřadnicovém systému by měla proto být
ds2 = − c2 dt2/γ2 + γ2 dr2 + r2dΩ2.
Úhlové rozměry jsou v obou metrikách nedotčeny. Výsledek tedy je:
ds2 = − c2(1 − rg/r) dt2 + dr2/(1 − rg/r) + r2dω2,
gij = diag {−c2(1 − rg/r), 1/(1 − rg/r), r2, r2 sin2θ}.
Tento vztah skutečně rigorózně odvodil Karl Schwarzschild z rovnic obecné relativity. Naše „odvození“ je jen jakýmsi náznakem. Použili jsme nerelativistický vztah pro energii a systém, který je inerciální jen lokálně. Úhlová část metriky je nedotčena (je to zjevné z „odvození“ pomocí padajícího systému – v úhlových směrech ke kontrakci nedochází). Časová část je ale nyní ovlivněna (v různých vzdálenostech od objektu jde čas různě) a radiální část metriky také. Ve velkých vzdálenostech od centrálního tělesa (rg>>r) přechází Schwarzschildova metrika v Minkowského metriku, časoprostor není zakřiven. Na Schwarzschildově poloměru se čas zastaví a radiální část metriky diverguje. Je to vlastnost zvoleného souřadnicového systému, který je pevný v prostoru. Padající pozorovatel by při průchodu Schwarzschildovým poloměrem nepozoroval nic zvláštního.

Schwarzschildovu metriku měla na plakátě i konference „Probing Strong Gravity Near Black Holes“, která probíhala v pražském Karolínu v roce 2010. Přijel na ní i objevitel první černé díry Paul Murdin.
Fridmanova-Lemaitrova-Robertsonova-Walkerova metrika
Když Albert Einstein hledal řešení rovnic obecné relativity pro vesmír vyplněný látkou s konstantní hustotou, ke svému zděšení zjistil, že gravitace, jakožto přitažlivá síla, způsobí zmenšování vzdáleností mezi objekty a následný kolaps vesmíru. Proto v roce 1917 do svých rovnic přidal tzv. kosmologický člen, který pomohl udržet rovnováhu a zajistil stacionární řešení, tj. neměnný vesmír, který byl v souladu s tehdejšími představami fyziků. V roce 1922 provedl ruský matematik, fyzik a meteorolog Alexandr Fridman detailnější výpočty, v nichž zjistil, že rovnováha mezi gravitačním přitahováním a kosmologickým členem je nestabilní a jakákoli malá porucha povede buď k expanzi vesmíru, nebo k jeho kolapsu. Bylo zjevné, že kosmologický člen situaci nezachrání. Obdobné řešení odvodil také belgický kněz abbé Georges Lemaître a z tohoto řešení ukázal dva roky před Hubblovým objevem expanze vesmíru (1929), že rychlost objektů měřená v konkrétním místě bude růst lineárně se vzdáleností. Místní časopis, ve kterém své objevy publikoval, nebyl mezi astronomy znám, a tak o Lemaîtrových výsledcích ostatní fyzici nevěděli. Existenci červeného posuvu spektra galaxií v důsledku expanze vesmíru také nezávisle předpověděl americký matematik a fyzik Howard Percy Robertson (1903–1961) v roce 1928. Detailní analýzu všech možných způsobů expanze vesmíru provedl na základě matematické teorie grup anglický matematik Arthur Geoffrey Walker (1909–2001) až v roce 1936. Uveďme zde tvar metriky expandujiícího vesmíru vyplněného látkou s konstantní hustotou v původním tvaru publikovaném Fridmanem:
ds2 = − c2dt2+ a2(t) [ dr2/(1 − kr2) + r2dω2],
gij = diag {−c2, a2(t)/(1 − kr2), a2(t) r2, a2(t) r2 sin2θ}.
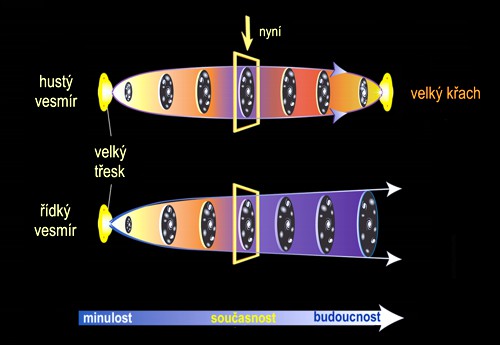
Osud vesmíru ve Fridmanově řešení závisí na hustotě vesmíru.
Skutečnost
je ale jiná, vesmír se v současnosti rozpíná zrychlenou expanzí.
