|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Kvantování prostoročasu – holografický vesmír
David Zoul
Makroskopická zkušenost nás vede k intuitivní představě elementárních částic coby nepatrných entit, které, pokud nemohou být geometricky bodové, jak jsme ukázali v předešlých bulletinech, by nejspíš měly vypadat jako drobné kuličky, neboť koule je v makrosvětě tím energeticky nejúspornějším tvarem, navíc s nejvyšším možným stupněm symetrie – ať kouli otáčíme libovolným směrem o libovolný úhel, vypadá stále stejně. Ačkoli nám poloklasické úvahy často ukazují nové směry, jimiž je třeba se v našem bádání ubírat, nemohou vést ve skutečnosti ke zcela přesným výsledkům, neboť zákony, jimiž se řídí mikrosvět, jsou dosti odlišné od zákonů makrosvěta. Pokud bychom nepostupovali důsledně kvantově mechanicky, zbloudili bychom brzy na scestí.

Prostorová vlnová funkce partonu. Mathematica.
|
Entropie – v termodynamice je definována vztahem dS = dQ/T, kde dQ je diferenciál tepla a T je absolutní teplota (1/T je integrační faktor). Takto zavedená entropie je na rozdíl od tepla úplným diferenciálem, její integrál nezávisí na cestě ve stavovém prostoru. Ve statistice má entropie význam logaritmické míry pravděpodobnosti realizace stavu, v kvantové teorii je logaritmickou mírou počtu kvantových stavů, kterými lze daný makroskopický stav realizovat. Entropie tak souvisí s „množstvím chaosu“ v systému. V informatice entropie popisuje množství informací. V uzavřeném systému může entropie jen růst. V termodynamické rovnováze dosáhne svého maxima. Holografický princip – představa, že informace o N-dimenzionální entitě je zapsatelná v N−k dimenzích. Název pochází z holografie, v níž se informace o třírozměrném objektu zapisují na dvojrozměrném hologramu, z něhož je možné původní objekt rekonstruovat. V matematice jsou ze znalosti hodnot komplexní funkce mající derivaci (tzv. holomorfní funkce) na hranici množiny určitelné její hodnoty v celé množině. Ve fyzice jsou vlastnosti černé díry určeny pouze jejím povrchem. Holografický princip je velmi atraktivní ve fyzice elementárních částic a v některých teoriích gravitace. Topologie – nauka o globálních vlastnostech a struktuře množin. Za topologicky ekvivalentní považujeme množiny, které lze spojitě deformovat jednu na druhou. Topologicky ekvivalentní nejsou množiny, lišící se přítomností „díry“, „slepením“ některých hraničních částí atd. Topologie vesmíru jako celku není známa. Rovnice obecné relativity nám umožňují jen sledování lokálních geometrických vlastností. Eukleidova geometrie – geometrický systém založený na definicích a axiomech, které publikoval Eukleidés v díle Základy. V Eukleidově geometrii je například součet úhlů v trojúhelníku vždy roven 180°. Minkowského geometrie – 4tyřrozměrný geometrický systém zavedený německým matematikem Hermanem Minkowskim roku 1908, v němž jako čtvrtý rozměr vystupuje čas a platí zde vztahy speciální teorie relativity – Lorentzovy transformace. V Minkowského geometrii je kupříkladu čtverec nad přeponou pravoúhlého trojúhelníka roven rozdílu čtverců nad oběma odvěsnami. Schwarzschildova geometrie – nejobecnější statické, sféricky symetrické, vakuové řešení Einsteinových rovnic gravitačního pole bez elektrického náboje. Řešení je pojmenováno podle německého fyzika Karla Schwarzschilda, který je publikoval v roce 1916. Popisuje jednu z tzv. neeukleidovských geometrií, ve kterých je kupříkladu součet úhlů v trojúhelníku obecně odlišný od 180°. |
Atomy hmoty pod drobnohledem
Výsledkem měření druhé mocniny momentu hybnostiMoment hybnosti – veličina popisující rotační pohyby těles. Jde o vektorový součin spojnice počátku souřadnicové soustavy a tělesa (radiusvektoru) s hybností tělesa. Velikost momentu hybnosti je rovna součinu hmotnosti tělesa, rychlosti tělesa, vzdálenosti tělesa od počátku souřadnic a sinu úhlu mezi radiusvektorem a směrem rychlosti. Při dané rychlosti a hmotnosti je moment hybnosti maximální pro kruhový pohyb a minimální (nulový) pro radiální pohyb od nebo ke středu soustavy (úhel v definičním vztahu je nulový). nebodové částice může být dle Schrödingerovy rovnice pouze některá z hodnot ℓ ( ℓ + 1) h2, kde ℓ ∈ N0. Výsledkem měření libovolné komponenty momentu hybnosti může být pouze celočíselný násobek h. Jestliže při měření druhé mocniny momentu hybnosti byla nalezena hodnota ℓ ( ℓ + 1) h2, potom výsledkem simultánního měření jeho jedné komponenty může být pouze některá z (2ℓ + 1) hodnot mh, kde m = ℓ, ℓ −1, … ,−ℓ. Tento fakt souvisí s tzv. prostorovým kvantováním. Moment hybnosti B, pro nějž platí
| || B || = [ ℓ ( ℓ + 1)]½ h , | (1) |
může s daným směrem n svírat pouze takové úhly θm, aby
| n·B = mh; m = -ℓ … ℓ , | (2) |
tj.
| cos θm = m / [ ℓ ( ℓ + 1)]½ . | (3) |
Prostorové kvantování odhaluje složité struktury – ne nepodobné atomovým a molekulovým orbitalům, pouze o 25 řádů menší – existující v samotných buňkách prostoročasu. Superpozicí těchto struktur se utvářejí prostorové vlnové funkce podobné té, kterou vidíme na úvodním obrázku.
Piškvorkový svět
Einsteinův žák, geniální fyzik a vizionář John Archibald Wheeler věřil, že všechna látková tělesa jsou složena z bitůbit – základní jednotka klasické informace, která nabývá dvou hodnot (ano/ne), (0/1), (pravda/nepravda) atd. Násobnou jednotkou je kilobit označující 210 = 1024 možností. Termín zavedl Claude Elwood Shanon coby zkratku anglického termínu binary digit. Fyzikální realizace bitu si žádá systém se dvěma dobře definovanými stavy – například logický obvod bez napětí a s napětím. informací, což vyjádřil ve svém známém sloganu „It from bit“. Podle něho měl bit, coby nejzákladnější jednotka informace, také tu nejmenší možnou velikost, odpovídající fundamentálnímu kvantu prostoru – Planckově buňce.
V minulých bulletinech na toto téma jsme si ukázali, že prostor může být rozdělen na Planckovy buňky, které tak vytvoří trojrozměrnou mřížku. V každé z těchto buněk pak může (ale také nemusí) sídlit jeden bit, který si můžeme představit jako nejzákladnější částici – parton. Další způsob, jak si znázornit tyto buňky, je představa obřích trojrozměrných piškvorek, jak nám ji přibližuje následující obrázek.
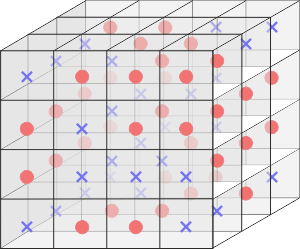
Wheelerova-Feynmanova představa celulárního prostoru
Podle Wheelerovy představy mohou fyzikální podmínky světa být v daném okamžiku vyjádřeny právě takovýmto stavem 3D piškvorků. Jelikož s časem se věci ve světě mění, musí se i kolečka a křížky v našem piškvorkovém světě časem přesouvat z jedné buňky do jiné. V jednom okamžiku může vzor vypadat jako na obrázku, v dalším okamžiku se může přeskupit.
V tomto Wheelerově světě informací se zákony fyziky skládají z pravidel určujících, jak se od jednoho okamžiku ke druhému mění konfigurace bitůbit – základní jednotka klasické informace, která nabývá dvou hodnot (ano/ne), (0/1), (pravda/nepravda) atd. Násobnou jednotkou je kilobit označující 210 = 1024 možností. Termín zavedl Claude Elwood Shanon coby zkratku anglického termínu binary digit. Fyzikální realizace bitu si žádá systém se dvěma dobře definovanými stavy – například logický obvod bez napětí a s napětím.. Taková pravidla, pokud by byla správně zkonstruována, by vlnám tvořeným z koleček a křížků v mřížce umožňovala šířit se napříč mřížkou a reprezentovat třeba světelné, nebo gravitační vlny. Veliký pevný kus složený z křížků (partonů) může ve svém okolí narušit šíření ostatních koleček a křížků, čímž bychom získali reprezentaci gravitačního pole těžkých těles. Wheelerův buněčný svět zaplněný planckovskými bity informací ovlivnil fyziky na mnoha úrovních. Jeho velkým zastáncem byl například Richard Feynman, který strávil hodně času konstruováním zjednodušených světů složených z bitů zaplňujících prostor. V tomto modelu je veškerý prostor tvořen krychlovou mřížkou o straně jedné buňky rovné Plackově délce.
Kinematika se v tomto modelu dociluje přeléváním křížků mezi jednotlivými buňkami, přičemž struktura stereomin (viz AB 43/2021) zůstává zachována, pokud mezi nimi nedochází k interakcím. Buňky označené křížky, nebo například přirozenými čísly (tj. nikoliv nulou) označujeme jako buňky aktivované. Každé aktivované buňce odpovídá v prostoročase kvantum energie Ey zvané parton, s nímž jsme se již seznámili v předešlém dílu. Buňky, jež jsou v daném časovém okamžiku nulové, představují tzv. inaktivní body. Jsou to oblasti bez projevené energie, vytvářející však prostor nezbytný pro zprostředkování jejího přenosu. Abychom si to blíže objasnili, musíme si nejprve povědět, jak kdysi jeden z Wheelerových studentů – izraelský fyzik Jacob Bekenstein – vypočetl entropiiEntropie – v termodynamice je definována vztahem dS = dQ/T, kde dQ je diferenciál tepla a T je absolutní teplota (1/T je integrační faktor). Takto zavedená entropie je na rozdíl od tepla úplným diferenciálem, její integrál nezávisí na cestě ve stavovém prostoru. Ve statistice má entropie význam logaritmické míry pravděpodobnosti realizace stavu, v kvantové teorii je logaritmickou mírou počtu kvantových stavů, kterými lze daný makroskopický stav realizovat. Entropie tak souvisí s „množstvím chaosu“ v systému. V informatice entropie popisuje množství informací. V uzavřeném systému může entropie jen růst. V termodynamické rovnováze dosáhne svého maxima. černé díryČerná díra – objekt, který kolem sebe zakřiví čas a prostor natolik, že z něho nemůže uniknout ani světlo. Část z nich vzniká kolapsem hvězdy v závěrečných fázích vývoje. Druhou skupinu tvoří obří černé díry sídlící v centrech galaxií. Rotující černé díry kolem sebe vytvářejí akreční disky látky a v ose rotace výtrysky vysoce urychlených částic. Paradoxně akreční disky i výtrysky, vznikající v bezprostředním okolí černé díry, velmi intenzivně vyzařují..

Jacob David Bekenstein (1947–2015)
Bekenstein cítil, že právě černé díryČerná díra – objekt, který kolem sebe zakřiví čas a prostor natolik, že z něho nemůže uniknout ani světlo. Část z nich vzniká kolapsem hvězdy v závěrečných fázích vývoje. Druhou skupinu tvoří obří černé díry sídlící v centrech galaxií. Rotující černé díry kolem sebe vytvářejí akreční disky látky a v ose rotace výtrysky vysoce urychlených částic. Paradoxně akreční disky i výtrysky, vznikající v bezprostředním okolí černé díry, velmi intenzivně vyzařují. v sobě skrývají cosi fundamentálně hlubokého a lákalo jej odhalení tajemství, jak černé díry zapadají do principů kvantové mechaniky a termodynamiky, které dělaly vrásky už Einsteinovi. Styl, jakým Bekenstein dělal fyziku, se velmi podobal tomu, jak ji dělal i Einstein. Oba byli schopni vyvodit dalekosáhlé důsledky, jež hluboce ovlivnily další vývoj fyziky, jen s málem matematiky, ale se spoustou přemítání nad základními principy a jejich fungováním ve vzájemných vztazích.
Bekenstein si představoval, kterak krouží okolo černé díry s kontejnerem plným horkého plynu, který na laně pozvolna spouští až k horizontu událostí, kde otevře spodní část kontejneru a nechá všechen horký plyn přetéci do černé díry. Protože podle tehdejších představ nebylo možné získat informaci o něčem, co již jednou pohltila černá díra, znamenalo to, že by tímto způsobem bylo možno z vesmíru nenávratně odčerpávat bitybit – základní jednotka klasické informace, která nabývá dvou hodnot (ano/ne), (0/1), (pravda/nepravda) atd. Násobnou jednotkou je kilobit označující 210 = 1024 možností. Termín zavedl Claude Elwood Shanon coby zkratku anglického termínu binary digit. Fyzikální realizace bitu si žádá systém se dvěma dobře definovanými stavy – například logický obvod bez napětí a s napětím. informaceInformace – veličina, která má různý význam v různých oborech. V technických vědách znamená zprávu zapsanou jako uspořádaný řetězec symbolů. Nejmenší informací je jeden bit odpovídající zápisu dvoustavové veličiny (0/1, ano/ne atd.). Ve fyzice může jít o cokoli, co je schopno ovlivnit stav systému. Informaci lze přenášet za pomoci vln nebo jiných signálů. Logaritmickou mírou informace obsažené v látce je entropie.. To je však v příkrém rozporu s velmi silným fyzikálním principem – druhým zákonem termodynamikyDruhý termodynamický zákon – zákon určující směr přírodních procesů. Lze ho formulovat mnoha způsoby: 1) existuje integrační faktor k diferenciálu tepla; 2) teplo nemůže samovolně proudit z chladnějšího na teplejší těleso; 3) entropie uzavřené soustavy roste, maxima dosáhne v termodynamické rovnováze; 3) nelze sestrojit trvale pracující termodynamický stroj, který by konal práci ochlazováním jediné lázně (perpetuum mobile druhého druhu)..
Bekenstein došel k závěru, že druhý termodynamický zákon stojí na příliš pevných základech na to, aby na něj šlo tak snadno rezignovat. Přišel proto s návrhem, že informaciInformace – veličina, která má různý význam v různých oborech. V technických vědách znamená zprávu zapsanou jako uspořádaný řetězec symbolů. Nejmenší informací je jeden bit odpovídající zápisu dvoustavové veličiny (0/1, ano/ne atd.). Ve fyzice může jít o cokoli, co je schopno ovlivnit stav systému. Informaci lze přenášet za pomoci vln nebo jiných signálů. Logaritmickou mírou informace obsažené v látce je entropie. musí nést samotný povrch černé díry. Čím víc informace pak skončí v černé díře, tím více se zvětší její povrch. Do veškeré informace vesmíru je tak nutno započíst rovněž i informaci obsaženou na površích černých děr.
Bekenstein uvažoval následovně: informace jde ruku v ruce s energií – informace má vždy co do činění s počtem přeskupení čehosi, co obsahuje energii, neboť podle Einsteina je veškerá hmota formou energie. Když proto Bekenstein vpustil horký plyn do černé díry, dodal jí energii a zvýšil tak její hmotnost i velikost.
Bekensteinovo následující odvození, že černé díry obsahují na svém povrchu bitybit – základní jednotka klasické informace, která nabývá dvou hodnot (ano/ne), (0/1), (pravda/nepravda) atd. Násobnou jednotkou je kilobit označující 210 = 1024 možností. Termín zavedl Claude Elwood Shanon coby zkratku anglického termínu binary digit. Fyzikální realizace bitu si žádá systém se dvěma dobře definovanými stavy – například logický obvod bez napětí a s napětím. informaceInformace – veličina, která má různý význam v různých oborech. V technických vědách znamená zprávu zapsanou jako uspořádaný řetězec symbolů. Nejmenší informací je jeden bit odpovídající zápisu dvoustavové veličiny (0/1, ano/ne atd.). Ve fyzice může jít o cokoli, co je schopno ovlivnit stav systému. Informaci lze přenášet za pomoci vln nebo jiných signálů. Logaritmickou mírou informace obsažené v látce je entropie. (tedy že musejí mít nenulovou entropiiEntropie – v termodynamice je definována vztahem dS = dQ/T, kde dQ je diferenciál tepla a T je absolutní teplota (1/T je integrační faktor). Takto zavedená entropie je na rozdíl od tepla úplným diferenciálem, její integrál nezávisí na cestě ve stavovém prostoru. Ve statistice má entropie význam logaritmické míry pravděpodobnosti realizace stavu, v kvantové teorii je logaritmickou mírou počtu kvantových stavů, kterými lze daný makroskopický stav realizovat. Entropie tak souvisí s „množstvím chaosu“ v systému. V informatice entropie popisuje množství informací. V uzavřeném systému může entropie jen růst. V termodynamické rovnováze dosáhne svého maxima.), patří k oněm jednoduchým, ale přesto hlubokým poznáním, která dokážou rázem změnit veškeré další směřování fyziky. Bekenstein se neptal přímo, kolik bitů by se mohlo ukrývat uvnitř černé díry dané velikosti. Namísto toho jej zajímalo, jak by se změnila velikost černé díry, kdyby do ní spadl jeden jediný bit informace. Je to podobné jako otázka, o kolik ve vaně stoupne voda, pokud do ní spadne jedna jediná molekula vody.
Tím pochopitelně vyvstala další otázka – jak můžeme přidat do černé díry jediný bit. Vzpomeňme si na kvantovou geometrodynamiku (viz AB 42/2021) a na odstavec, kde jsme si říkali, že rozlišovací schopnost optického mikroskopu je vždy srovnatelná s vlnovou délkou použitého světla, a pokud budeme vlnovou délku použitého světla neustále zkracovat, nakonec vytvoříme miniaturní černé díry o velikosti Planckových buněk, čímž je zároveň určena zrnitost prostoru. Trik, kterého Bekenstein využil, byl založen na velmi podobném, pouze obráceném principu. Použil foton s vlnovou délkou srovnatelnou s poloměrem horizontu rg. Větší vlnové délky fotonů se totiž do černé díry nevejdou – pouze se odrazí od Schwarschildovy sférySchwarzschildova sféra – myšlená sféra pojmenovaná podle německého fyzika Karla Schwarzschilda (1873–1916), který na základě rovnic obecné teorie relativity ukázal, že existuje dolní hranice pro poloměr statického tělesa. Zhroutí-li se těleso pod sféru vymezenou tímto poloměrem (tzv. Schwarzschildovu sféru), jeho hroucení dle OTR pokračuje až k singularitě. Pro vnějšího pozorovatele pak sféra představuje horizont událostí, neboť úniková rychlost z jejího povrchu je rovna rychlosti světla., ale nespadnou do ní. Energie fotonu, nesoucího do černé díry jeden bit informace, je tedy dána vztahem
| E = hc/rg . | (4) |
S tím související změna hmotnosti černé díry je
| Δm = h/rg c . | (5) |
Změna povrchu černé díry pak bude
| ΔA = 4π/Δr 2g = 8πhG/c3 = 8πℓ 2h . | (6) |
Bekenstein tak dospěl k překvapivému závěru, že jeden bit informace zvýší povrch horizontu libovolné černé díry vždy o 8π násobek Planckovy plochy. Bylo tedy jisté, že nějakým tajemným způsobem se skrývá v principech kvantové mechaniky a obecné teorie relativity spojení mezi bity informací a titěrnými Planckovými ploškami na horizontu událostí.
Představíme-li si, že stavíme černou díru bit po bitu, jako když bychom napouštěli vanu molekulu po molekule, pokaždé když přidáme bit informace, vzroste povrch horizontu o 8π násobek Planckovy plochy. Jakmile černou díru dostavíme, bude povrch horizontu odpovídat celkovému počtu informací skrytých uvnitř. Přesně toto zjištění znamenalo triumf Bekensteinova modelu, který můžeme shrnout slovy: Entropie černé díry měřená v bitech je úměrná povrchu jejího horizontu měřeného v Planckových jednotkách.
Bekenstein ukázal, že horizont černé díry je hustě pokrytý nestlačitelnými bity informace. Ve skutečnosti jsou tyto plošky jen stěnami Planckových buněk našeho piškorkového světa, jejichž hrana je elementárním krokem v prostoru – krokem, jímž je prostor kvantován. Horizont černé díry tak netvoří pouze dvourozměrná plocha, ale je to vrstva elementárních prostorových buněk, nesoucích bity informace.
Svět jako americká kobliha
Jak ukážeme dále, celý prostor ve skutečnosti připomíná nitro jedné ohromné černé díry, jejíž horizont je rovněž tvořen takovouto podivuhodnou vrstvou, na níž jsou uloženy veškeré bity z prostoru. Geometrickou zvláštností našeho piškvorkového světa je skutečnost, že ačkoliv nemá žádnou hranici, je prostorově omezen v tom smyslu, že obsahuje pouze konečné množství buněk – kvant prostoru. Pokud některý objekt míří k hranici, objeví se před dosažením této hranice na opačném konci prostoru. V zásadě je tak možné, že vaše hlava se právě v okamžiku, kdy čtete tyto řádky, nalézá přesně na opačné straně vesmíru, než zbytek vašeho těla vzdálený řádově 1027 metrů od vaší hlavy, aniž byste zaregistrovali cokoliv podivného. Vzhledem k hexaedrické symetrii prostoru generovaného kvantovou mřížkou (piškvorkového světa) je takováto vlastnost duální útvaru, zvanému hypertorus. Třírozměrný prostor přitom tvoří jeho hranici obklopující hyperprostor uvnitř. Souřadnice v tomto duálním obrazu piškvorkového světa se dělí na toroidální, poloidální a hyperoidální.

Obr. 1: Umělecké ztvárnění prostoru s toroidální topologií
Stojí za zdůraznění, že v tomto pětirozměrném (čtyři prostorové + jedna časová dimenze) modelu s vícenásobně souvislouJednoduše souvislá množina – množina, která nevypadá jako „ementál“. Nemá žádné díry ani držadla, každou uzavřenou křivku lze stáhnout do bodu. topologiíTopologie – nauka o globálních vlastnostech a struktuře množin. Za topologicky ekvivalentní považujeme množiny, které lze spojitě deformovat jednu na druhou. Topologicky ekvivalentní nejsou množiny, lišící se přítomností „díry“, „slepením“ některých hraničních částí atd. Topologie vesmíru jako celku není známa. Rovnice obecné relativity nám umožňují jen sledování lokálních geometrických vlastností. se vytrácí hranice prostoru, která existuje ve čtyřrozměrném duálním modelu. V AB 30/2021 (Petr Kulhánek: Může být vesmír konečný?) naleznete pojednání o prvních observačních údajích, jež by mohly potvrzovat tuto předpověď.
Svět jako hologram
Stlačíme-li hmotu pod její gravitační poloměr rg, úniková rychlost na jejím povrchu bude rovna rychlosti světla ve vakuu. To znamená, že ani světlo nebude schopno pronikat ven ze sférické oblasti vymezené gravitačním poloměrem – z černé díryČerná díra – objekt, který kolem sebe zakřiví čas a prostor natolik, že z něho nemůže uniknout ani světlo. Část z nich vzniká kolapsem hvězdy v závěrečných fázích vývoje. Druhou skupinu tvoří obří černé díry sídlící v centrech galaxií. Rotující černé díry kolem sebe vytvářejí akreční disky látky a v ose rotace výtrysky vysoce urychlených částic. Paradoxně akreční disky i výtrysky, vznikající v bezprostředním okolí černé díry, velmi intenzivně vyzařují.. Protože žádný signál se nemůže v prostoročase šířit vyšší rychlostí, než je rychlost světla ve vakuu, znamená to, že nitro černé díry je mohutnou gravitací odříznuto od okolního regulárního prostoročasu. Zatímco do nitra mohou pronikat částice velmi snadno, ven by se dle klasické fyziky, tj. obecné teorie relativityObecná relativita – teorie gravitace publikovaná Albertem Einsteinem v roce 1915. Její základní myšlenkou je tvrzení, že každé těleso svou přítomností zakřivuje prostor a čas ve svém okolí. Ostatní tělesa se v tomto pokřiveném světě pohybují po nejrovnějších možných drahách, tzv. geodetikách., nemělo dostat nic. Jedná se tedy o oblast, v níž je relativistický prostoročas úplně zakřiven, tj. zcela uzavřen sám do sebe.
Kvantověmechanický rozbor celého problému provedený v roce 1974 Stephenem Hawkingem však odhalil pozoruhodnou skutečnost, že černé díry ve skutečnosti vyzařují energii, ačkoliv je to v rozporu s obecbou teorií relativity.

Stephen William Hawking (1942–2018). Zdroj: Indiana News.
Hranice černé díry, zvaná Schwarzschildova sféraSchwarzschildova sféra – myšlená sféra pojmenovaná podle německého fyzika Karla Schwarzschilda (1873–1916), který na základě rovnic obecné teorie relativity ukázal, že existuje dolní hranice pro poloměr statického tělesa. Zhroutí-li se těleso pod sféru vymezenou tímto poloměrem (tzv. Schwarzschildovu sféru), jeho hroucení dle OTR pokračuje až k singularitě. Pro vnějšího pozorovatele pak sféra představuje horizont událostí, neboť úniková rychlost z jejího povrchu je rovna rychlosti světla., není o nic tlustší než jedna Planckova délka. Částice, která se vytvoří těsně pod touto hranicí, ji může překonat a proniknout tak do regulárního prostoročasu pouze za předpokladu, že na kratičký okamžik bude schopna letět nadsvětelnou rychlostí. Podle kvantové teorie tomu vůbec nic nebrání. Heisenbergovy relace neurčitostiRelace neurčitosti – v mikrosvětě není možné současně změřit polohu a hybnost objektů. Změření jedné veličiny naruší měření druhé veličiny. Čím přesněji zjistíme polohu, tím menší informaci budeme mít o hybnosti a naopak. Jde o principiální zákonitost kvantového světa, která souvisí s nekomutativností veličin na elementární úrovni. Relace neurčitosti objevil Werner Heisenberg. Stejné relace platí také mezi energií a časovým intervalem. Ve vakuu mohou po velmi krátkou dobu vznikat ve shodě s relacemi neurčitosti fluktuace (objekty) o určité energii. Čím vyšší energie, tím kratší doba života těchto fluktuací. Dále relace platí i pro jakoukoli zobecněnou souřadnici a její hybnost. Může jít například o nějaké pole, které nemůže mít současně nulovou hodnotu a nulovou hybnost, což vede k jeho vakuovým fluktuacím. totiž ukazují, že průměrná rychlost částice podléhá na krátkých prostorových a časových intervalech lokálním fluktuacím.
Částice s tzv. nulovou klidovou hmotností, jež se dle klasické fyziky pohybuje přesně rychlostí světla, tedy ve skutečnosti musí dodržovat tuto mezní rychlost pouze v průměru, tj. na prostorových a časových intervalech dostatečně dlouhých ve srovnání s Planckovou délkou a Planckovým časem.
Na vzdálenostech řádově srovnatelných s tloušťkou Schwarzschildovy sféry však dochází ke značným odchylkám od této střední hodnoty rychlosti fotonů a dalších částic. Pokud se zde některé fotony mohou pohybovat například podsvětelnou rychlostí, pak jiné fotony tu musí dosahovat naopak lokálně nadsvětelných rychlostí, aby bylo možno zprůměrováním rychlostí všech fotonů nakonec dospět k hodnotě velmi blízké rychlosti světla.
Částice, které vznikly uvnitř černé díry v dostatečné blízkosti Schwarzschildovy sféry, tedy mají možnost na krátkou dobu překonat rychlost světla a uniknout ven. Poté však musí svoji rychlost znovu snížit na podsvětelnou hodnotu, aby jejich průměrná rychlost nepřekročila maximální povolenou hodnotu c. V této fázi mohou být některé částice, kterým se již podařilo uniknout skrze Schwarzschildovu sféru ven, opět vtaženy do útrob černé díry působením mohutných gravitačních sil. Pravděpodobnost, že se tak stane, je nepřímo úměrná tomu, jak rychle klesá intenzita gravitačního pole se vzdáleností od Schwarzschildovy sféry. Tento pokles intenzity gravitačního pole je nepřímo úměrný čtverci poloměru černé díry rg , tedy v podstatě ploše horizontu. Tedy čím je černá díra menší, tím rychleji vyzařuje energii do prostoru. Čím více energie ~ hmoty vyzáří za jednotku času, tím více se zmenší její poloměr, a tím více energie vyzáří v následujícím okamžiku. Teoretický výpočet ukazuje, že černá díra má entropii
| S = (kB/4ℓ 2h) A , | (7) |
kde A je plocha horizontu, jenž vyzařuje jako absolutně černé těleso zahřáté na termodynamickou teplotu
| T = hc3/8πkBGM . | (8) |
Vidíme, že entropie černé díry je úměrná počtu Planckových ploch ℓ 2h, kterými lze pokrýt horizont černé díry (s koeficientem kB/4). EntropieEntropie – v termodynamice je definována vztahem dS = dQ/T, kde dQ je diferenciál tepla a T je absolutní teplota (1/T je integrační faktor). Takto zavedená entropie je na rozdíl od tepla úplným diferenciálem, její integrál nezávisí na cestě ve stavovém prostoru. Ve statistice má entropie význam logaritmické míry pravděpodobnosti realizace stavu, v kvantové teorii je logaritmickou mírou počtu kvantových stavů, kterými lze daný makroskopický stav realizovat. Entropie tak souvisí s „množstvím chaosu“ v systému. V informatice entropie popisuje množství informací. V uzavřeném systému může entropie jen růst. V termodynamické rovnováze dosáhne svého maxima. černé díry je zároveň maximální entropií, kterou lze „vtěsnat“ do daného objemu uzavřeného uvnitř plochy velikosti A. Jinými slovy, černá díra představuje objekt, který nejefektivněji soustřeďuje entropii – plocha jejího horizontu A je nejmenším možným povrchem prostorové oblasti, v níž se hmota dané entropie S může nacházet.
V klasické termodynamice je entropie přímo úměrná objemu zaplněnému látkou. V kvantové fyzice gravitace je však entropie přímo úměrná povrchu, takže do daného objemu je možno „zakódovat“ podstatně méně informace, než by odpovídalo klasické představě. Dvojrozměrná plocha horizontu černé díry nese veškerou informaci o (trojrozměrných) konfiguracích pohlcené hmoty v černé díře, podobně jako dvojrozměrný hologramHolografie – forma záznamu obrazu, která umožňuje zachytit jeho trojrozměrnou strukturu na dvourozměrný obrazový nosič neboli hologram (fotografická deska, binární záznam) a jeho opětovnou rekonstrukci. Na hologram se zaznamenává jak intenzita, tak fáze světla. Holografii objevil Dennis Gabor v roce 1948, kvalitní hologramy byly ale pořízeny až po objevu laseru. V elektronovém mikroskopu lze pořídit elektronový hologram, v němž je zaznamenáno jak množství elektronů prošlých vzorkem, tak fáze jejich hmotové vlny. Fáze elektronových vln je citlivá na magnetické pole, proto je možné z elektronového hologramu určit průběh magnetických siločar ve vzorku. nese informace o trojrozměrném objektu. Tato skutečnost je proto často označována jako holografický princip. Holografický principHolografický princip – představa, že informace o N-dimenzionální entitě je zapsatelná v N−k dimenzích. Název pochází z holografie, v níž se informace o třírozměrném objektu zapisují na dvojrozměrném hologramu, z něhož je možné původní objekt rekonstruovat. V matematice jsou ze znalosti hodnot komplexní funkce mající derivaci (tzv. holomorfní funkce) na hranici množiny určitelné její hodnoty v celé množině. Ve fyzice jsou vlastnosti černé díry určeny pouze jejím povrchem. Holografický princip je velmi atraktivní ve fyzice elementárních částic a v některých teoriích gravitace. byl později dále zobecněn v souvislosti s budováním kvantových teorií gravitace: Informaci o systému uvnitř objemu V lze lokalizovat na povrch tohoto objemu, přičemž hustota informace nepřesahuje jeden bit na Planckovu plochu ℓ 2h.
Firewall černých děr
Původně se zdálo, že všechny černé díry, ať již vznikly těmi nejrozličnějšími způsoby, z těch nejrozmanitějších forem hmoty jaké si jen lze představit (včetně čisté gravitace v podobě koncentrovaných gravitačních vln), se navenek makroskopicky projevují vnějším polem nesoucím pouze tři elementární informace o vlastnostech hmoty, z níž černá díra vznikla. Těmito informacemi jsou:
|
Všechny ostatní informace jsou dle předpovědi obecné relativity horizontem odříznuty od okolního prostoročasu a jsou tudíž navždy ztraceny z vesmíru. Černé díry, jakkoli rozmanitého původu, by pak byly od sebe makroskopicky nerozlišitelné, mají-li stejnou hmotnost, náboj a moment hybnosti. Těmito svými vlastnostmi černé díry připomínají elementární částice, které se taktéž projevují pouze několika základními pozorovatelnými, jimiž jsou klidová hmotnost, elektrický náboj, spinSpin – vlastní (vnitřní) rotační moment částice souvisící s Lorentzovou symetrií. Pro částici v centrálním poli se přirozeným způsobem skládá s momentem hybnosti. Částice s nenulovým spinem se mohou chovat jako elementární magnetické dipóly μ, aniž by měly elektrický náboj. Takové částice reagují na vnější magnetická pole., popřípadě několik málo dalších kvantových čísel. Stejně jako černé díry, i elementární částice jsou vzájemně nerozlišitelné, pokud se od sebe neliší ve výše jmenovaných nezávislých pozorovatelných.
Výsledky teoretického výzkumu v uplynulých letech však ukázaly, že informace se v černé díře ve skutečnosti neztrácejí. Makroskopické informace jsou pouze rozloženy až na jejich vlastní kvantovou podstatu a poté lokalizovány na horizontu, odkud mohou být opět emitovány zpět do vesmíru kvantovou evaporací. Černá díra je tedy charakterizována nejen makroskopickými stavovými veličinami jako je hmotnost, moment hybnosti a elektrický náboj (jak původně předpokládali Wheeler a Hawking), ale též mikroskopickými stavovými veličinami (kvantovými čísly a charakteristikami) veškerých částic, které ji vytvořily.
Nejjednodušší případ, který byl studován nejdříve, je statická extrémní elektricky nabitá černá díra v pěti dimenzích. Extrémní elektricky nabité černé díry jsou teoretickými konstrukcemi černých děr, jejichž elektrický náboj je tak velký, že se elektrická odpudivá síla na horizontu vyrovná s přitažlivou silou gravitační. Nabité částice pak mohou být zpod horizontu extrémní černé díry mohutnou elektrickou silou doslova vystřelovány do okolního prostoru.
Andrew Strominger a Cumrun Vafa spočítali, že pro velké hodnoty náboje souhlasí entropieEntropie – v termodynamice je definována vztahem dS = dQ/T, kde dQ je diferenciál tepla a T je absolutní teplota (1/T je integrační faktor). Takto zavedená entropie je na rozdíl od tepla úplným diferenciálem, její integrál nezávisí na cestě ve stavovém prostoru. Ve statistice má entropie význam logaritmické míry pravděpodobnosti realizace stavu, v kvantové teorii je logaritmickou mírou počtu kvantových stavů, kterými lze daný makroskopický stav realizovat. Entropie tak souvisí s „množstvím chaosu“ v systému. V informatice entropie popisuje množství informací. V uzavřeném systému může entropie jen růst. V termodynamické rovnováze dosáhne svého maxima. (definovaná jako S = log N, kde N je počet kvantových stavů, ve kterých systém může být) s Bekensteinovou-Hawkingovou předpovědí. Ukázalo se, že stupně volnosti jsou v černé díře skutečně rozptýleny po povrchu.

Horní řada: Andrew Strominger (*1955); Cumrun Vafa (*1960)
Dolní řada: Curtis Gove Callan, Jr. (*1942); Gerardus 't Hooft (*1946)
Krátce po publikování Stromingerovy a Vafovy práce zobecnili Curtis Callan a jeho někdejší doktorand Juan Maldacena výpočet pro případ obecné černé díry ve 4D, stejně jako pro rotující černé díry. Na rozdíl od Hawkinga, který v roce 1974 provedl svůj výpočet semiklasickým způsobem, za použití kvantové teorie pole i klasické obecné relativity, Callan s Maldacenou použili důsledně pouze kvantový přístup. Výpočty byly dále nezávisle potvrzeny skupinou indických teoretiků a následně dalšími skupinami teoretiků z celého světa a staly se široce přijímaným fyzikálním principem. Celá situace je velmi podobná hologramu v tom smyslu, že plocha udržuje informaci o celém prostoru.
Díky principu ekvivalence musí tento princip platit nejen pro černou díru, ale pro úplně všechny fyzikální systémy, neboť dynamika jakéhokoli fyzikálního systému vypadá úplně stejně jako dynamika systému padajícího do ohromné černé díry, jejíž geometrie na horizontu je téměř plochá. To přivedlo v roce 1994 holandského fyzika Gerarda ´t Hoofta a amerického fyzika Lennyho Susskinda k závěru, že všechny stupně volnosti, v nichž je uložena informace o všem na světě, se dají lokalizovat na povrch prostoru, v němž žijí – jsou projektovány na dvourozměrnou plochu obklopující vesmír. Více se tomuto tématu budeme věnovat v příštím dílu.
Z toho, co jsme si až dosud řekli o holografickém principuHolografický princip – představa, že informace o N-dimenzionální entitě je zapsatelná v N−k dimenzích. Název pochází z holografie, v níž se informace o třírozměrném objektu zapisují na dvojrozměrném hologramu, z něhož je možné původní objekt rekonstruovat. V matematice jsou ze znalosti hodnot komplexní funkce mající derivaci (tzv. holomorfní funkce) na hranici množiny určitelné její hodnoty v celé množině. Ve fyzice jsou vlastnosti černé díry určeny pouze jejím povrchem. Holografický princip je velmi atraktivní ve fyzice elementárních částic a v některých teoriích gravitace., by se mohlo zdát, že černé díry jsou obklopeny jakousi magickou vrstvou extrémní hustoty a (pro volně padající pozorovatele, letící rychlostí blízkou rychlosti světla vstříc Hawkingově radiaci horizontu) rovněž teploty, nesoucí v sobě veškeré informace z nitra černé díry. Vžilo se pro ni označení firewall černé díry. Jak si však vzápětí ukážeme, tak tomu ve skutečnosti není. Soustava spojená s Bobem, volně padajícím do černé díry, totiž již není popsána Schwarzschildovou geometrií, jako je tomu v případě Alice, která celý Bobův pád sleduje z bezpečného povzdálí. Soustavu spojenou s volně padajícím Bobem popisuje tzv. Kruskalova-Szekeresova souřadnicová soustava.
Některé základní rysy Schwarzschildovy geometrie v Kruskalových-Szekeresových souřadnicích jsou schématicky znázorněny na Kruskalově diagramu (což je prostoročasový diagram v Kruskalových souřadnicích) na Obr. 2. Z obrázku je patrno, že metrikaMetrika – matematická struktura zobecňující pojem vzdálenosti dvou bodů. Definuje nejkratší vzdálenost mezi dvěma body v obecném (tzv. metrickém) prostoru. Tvoří-li metrický prostor například povrch koule, potom nejkratší spojnicí mezi libovolnými dvěma body tohoto prostoru je část kružnice (oblouk). Metrickým prostorem je i zakřivený prostoročas obecné relativity, a metrikou tohoto prostoru pak rozumíme nejkratší prostoročasový interval mezi dvěma událostmi v tomto prostoročase. Schwarzschildovy geometrie v Kruskalových souřadnicích je regulární všude s výjimkou středu r = 0 (kde se jedná o skutečnou fyzikální singularitu neodstranitelnou žádnou transformací souřadnicové soustavy).
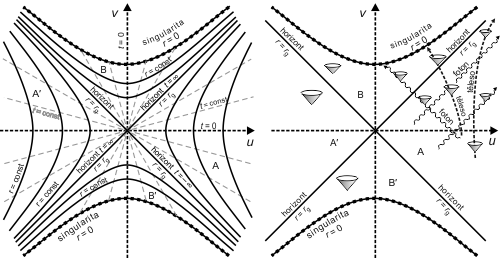
Obr. 2: Kruskalův prostoročasový diagram popisující Schwarzschildovu geometrii. Nalevo: Souřadnicová síť ve vztahu ke Schwarzschildovým souřadnicím r a t. Napravo: Celková struktura prostoročasu a pohyb testovacích částic a fotonů. A je vnější asymptoticky rovinná oblast, B je vnitřní oblast pod horizontem.
Singularita r = 0 je zde znázorněna dvěma oddělenými hyperbolami v2 – u2 = 1. Horizont je tvořen dvěma přímkami u = ±v. Vnější oblast černé díry je vyjádřena nerovností u2 > v2, což opět popisuje dvě vnější oblasti. Radiální světelné geodetiky jsou přímky vedené pod úhlem 45° k osám Kruskalovy soustavy. Tato vlastnost je velmi výhodná, protože světelné kužely vypadají úplně stejně jako v diagramu Minkowského rovinného prostoročasu speciální relativity. Reálná hmotná tělesa se tedy mohou v tomto Kruskalově diagramu pohybovat pouze pod úhlem menším než 45° od svislé osy (uvnitř prostoročasových světelných kuželů).

Martin David Kruskal (1925–2006), George Szekeres (1911–2005).
Fotografie: Nick Romaneniko, David Harvey..
Velmi podivné je to, že z původního Schwarzschildova řešení obsahujícího jen jednu asymptoticky rovinnou vnější oblast, jeden horizont a jednu singularitu r = 0, jsme přechodem ke Kruskalovým souřadnicím dostali prostoročas se dvěma vnějšími oblastmi, dvěma horizonty a dvěma singularitami. Vysvětlením je, že prostoročas získaný přechodem ke Kruskalovým souřadnicím je úplnou analytickou extenzí původní Schwarzschildovy geometrie, tedy obecnějším řešením Einsteinových rovnic obecné relativity, než jakým je Schwarzschildova metrikaMetrika – matematická struktura zobecňující pojem vzdálenosti dvou bodů. Definuje nejkratší vzdálenost mezi dvěma body v obecném (tzv. metrickém) prostoru. Tvoří-li metrický prostor například povrch koule, potom nejkratší spojnicí mezi libovolnými dvěma body tohoto prostoru je část kružnice (oblouk). Metrickým prostorem je i zakřivený prostoročas obecné relativity, a metrikou tohoto prostoru pak rozumíme nejkratší prostoročasový interval mezi dvěma událostmi v tomto prostoročase. reprezentovaná pouze pohledem Alice z bezpečné vzdálenosti. Skutečný prostoročas pozorovaný padajícím Bobem, který je řešením Einsteinových rovnic pro ostrovní sféricky symetrický případ, je rozsáhlejší varietou, než by se dalo očekávat z původního řešení ve Schwarzschildových souřadnicích. Schwarzschildovy souřadnice jsou schopny obsáhnout jen část této úplné variety, zatímco Kruskalovy souřadnice ji obsáhnou celou.

Obr. 3: Znázornění geometrické struktury řezu (prostorové hyperplochy) v = t = 0 Schwarzschildovým prostoročasem ve formě vnoření do pomocného trojrozměrného eukleidovského prostoru. Tento pomocný trojrozměrný prostor nemá fyzikální význam (je pouze prostředkem pro znázornění); význam má pouze vnitřní geometrie vnořené plochy, která ukazuje dvě asymptoticky rovinné oblasti A a A′ spojené Einsteinovým-Rosenovým mostem. Zdroj: Digitale Welt/ Rost-9D.
Jestliže oblast A na Obr. 2 je původní vnější asymptoticky rovinnou oblastí Schwarzschildovy geometrie („náš vesmír“), objevuje se ještě jedna zrcadlově obrácená asymptoticky rovinná oblast A′ na druhé straně diagramu, jakýsi „druhý vesmír“. Vezmeme-li si řez Kruskalovým diagramem podél osy u (tedy řez t = 0 podle Obr. 2), vidíme, že kulové plochy r = const. s ubývajícím r nejprve normálně zmenšují svoje plochy, avšak ne k nule. Potom znovu rostou, jako kdyby se rozšiřovaly do druhého asymptoticky rovinného prostoru. Názorně je tato situace zachycena na Obr. 3, který je vnořením řezu t = 0 s jedním vynechaným rozměrem do pomocného trojrozměrného prostoru. Úplná geometrie obsahuje v časovém řezu určitý „tunel“, zvaný Einsteinův-Rosenův most, spojující dva různé asymptoticky rovinné vesmíry. Jak je jasně vidět z Kruskalova diagramu, Einsteinovým-Rosenovým mostem nemůže nikdo proniknout do druhého (zrcadlově obráceného) vesmíru, protože by se musel pohybovat nadsvětelnou rychlostí, aby stačil uniknout singularitě.

Horní řada: Albert Einstein (1879–1955); Herman Minkowski
(1864–1909)
Dolní řada: Karl Schwarzschild (1873–1916); Nathan Rosen (1909–1995)
Za předpokladu obvyklé eukliedovské globální topologie by takový most mohl spojovat i dvě různá místa jednoho vícenásobně souvislého vesmíru, jak ukazuje Obr. 4 – tehdy hovoříme o tzv. červí díře.

Obr. 4: Geometrické znázornění červí díry prostřednictvím diagramu vnoření.
Zdroj: Andrzej Wojcicky/Science Photo Library/Getty Images.
Další zajímavou vlastností Schwarzschildova řešení, která je vidět z Kruskalova diagramu, je dynamický charakter geometrie v oblasti pod horizontem. Sledujeme-li časové řezy (rovnoběžné s osou u) Kruskalovým diagramem postupně od velkých záporných hodnot v až do velkých kladných hodnot v (tj. ve směru časové evoluce), spatříme zpočátku dva nesouvisející asymptoticky rovinné vesmíry, z nichž každý má svoji singularitu r = 0. Jakmile řez přestane procházet dolní (minulou) singularitou, objeví se mezi oběma vnějšími oblastmi Einsteinův-Rosenův most. Tento most se bude rozšiřovat (maximální bude v řezu t = 0) a pak zase zužovat, až nakonec při dotyku řezu s horní singularitou zanikne a opět zbudou dva nesouvisející vesmíry se svými singularitami. Lze říci, že most zanikne tak rychle, že jím žádný reálný objekt nestihne proniknout do druhého vesmíru (skončí vždy v singularitě). Geometrie Schwarzschildova řešení má pod horizontem dynamický charakter vlivem toho, že zde v důsledku výměny rolí časových a prostorových metrických komponent úlohu časové evoluce přebírá „evoluce“ prostorová.
Je na první pohled vidět, že topologie nebude eukleidovská v bodě r = 0, kde je singularita; mohlo by se ale zdát, že toto je jediný rozdíl od obyčejných topologických vlastností. Úplná extenze však ukazuje zcela jinou globální topologii – dva různé asymptoticky rovinné „vesmíry“ spojené „mostem“, který má dynamický charakter. Přechodem ke Kruskalovým souřadnicím, to jest ke vztažné soustavě spojené s volně padajícími testovacími částicemi, původní pseudosingularita na Schwarzschildově sféřeSchwarzschildova sféra – myšlená sféra pojmenovaná podle německého fyzika Karla Schwarzschilda (1873–1916), který na základě rovnic obecné teorie relativity ukázal, že existuje dolní hranice pro poloměr statického tělesa. Zhroutí-li se těleso pod sféru vymezenou tímto poloměrem (tzv. Schwarzschildovu sféru), jeho hroucení dle OTR pokračuje až k singularitě. Pro vnějšího pozorovatele pak sféra představuje horizont událostí, neboť úniková rychlost z jejího povrchu je rovna rychlosti světla. vymizí. Geometrie samotného prostoročasu je na Schwarzschildově sféře zcela regulární, pozorovatel může přes Schwarzschildovu sféru volně projít během konečného intervalu vlastního času, nezjistí zde lokálně vůbec nic zvláštního a bude pokračovat dál ve svém pohybu. Zvláštnost prostoročasové geometrie na Schwarzschildově sféře nespočívá tedy v nějakých nenormálních lokálních vlastnostech, má význačnou globální vlastnost – je horizontem událostíHorizont událostí – rozhraní u černé díry, po jehož překročení již není možné vyslat jakýkoli signál vnějšímu pozorovateli. Rozměr horizontu událostí určil z obecné relativity Karl Schwarzschild v roce 1916, proto často hovoříme o tzv. Schwarzschildovu poloměru černé díry. U rotující černé díry spočítal tvar horizontu událostí Roy Kerr v roce 1963..
V roce 1976 předpověděl William Unruh na základě kvantové teorie pole existenci jakési kinematické obdoby Hawkingova záření, pro jehož tvorbu není však tentokráte zapotřebí žádný globální horizont událostí. Podrobně se lze o jevu dočíst například v AB 35/2014 (Miroslav Havránek: Unruhův jev – tepelné záření vakua)

William George Unruh (*1945). Zdroj: UBC.
Jestliže je entropie černých děr úměrná povrchu, nikoli objemu, a zrychlující pozorovatelé vnímají horizonty událostí na prakticky libovolných místech – podle zvoleného zrychlení a polohy pozorovatele – a tyto horizonty rovněž vyzařují záření obdobné Hawkingovu, pak by kolem každého objemu měla jít nakreslit myšlená uzavřená plocha taková, že všechny informace o objektech uvnitř půjdou popsat pouze fyzikou na povrchu této plochy.
Navíc to vypadá, že ne každý pozorovatel může měřit na systému totéž, což velmi dobře ilustruje rozdílný pohled Alice a Boba v našem myšlenkovém experimentu s pádem do černé díry. Z hlediska padajícího Boba se na horizontu nestane nic zvláštního – jde jen o normální oblast prázdného a lokálně plochého prostoročasu. Z hlediska Alice ale každého padajícího pozorovatele musí usmažit Hawkingovo záření vycházející z horizontu, kterému volně padající pozorovatel letí vstříc se stále se zvyšující rychlostí, která se již na horizontu má rovnat rychlosti světla. Dá se ukázat, že paradox není rozřešitelný v rámci standardního modelu, ani obecné relativity. Z těchto indicií usuzujeme, že k dokončení kvantové gravitace není potřeba nic menšího než předefinování kvantového stavu tak, aby zahrnoval existenci horizontů událostí a toho, že některé informace jsou pro některé pozorovatele nedostupné a různí pozorovatelé na stejnou otázku mohou dostat různou odpověď, pokud ji v principu nemají, jak porovnat.
Horizont černé díry není jedinou hranicí pro šíření elektromagnetického záření. I v laboratorních pokusech se šířením světla existují oblasti, za které se světlo dostat nemůže. Typickým příkladem mohou být experimenty se zpomalováním nebo zastavováním světla. V médiu, kterým se světlo šíří, vznikají „horizonty“, za které se světlo dostat nemůže. Zajímavou otázkou je, zda i na těchto laboratorních horizontech může dojít ke genezi Hawkingova záření. Podle experimentů provedených pracovníky Univerzity v Milánu a italského Národního ústavu pro jaderný výzkum (INFN) to vypadá, že ano. Podrobnosti viz například v AB 35/2010 (Petr Kulhánek: Existuje laboratorní analogie Hawkingova vypařování?)
Tento, i další experimenty naznačují, že holografický princip je mnohem hlubším fyzikálním zákonem, než jsme si dosud mysleli. Nejen horizont černé díry může nést informaci o veškerém dění uvnitř odpovídající oblasti prostoru, kterou obklopuje, ale doslova každý horizont (byť i zdánlivý – čitelný jen pro některé pozorovatele, kteří se momentálně pohybují tím správným způsobem) nese veškerou informaci o událostech probíhajících v prostoru, jehož hranici tvoří.
Bob, padající v utržené kabině výtahu volně do černé díry, je ve své soustavě inerciálním pozorovatelem – nepociťuje žádnou vnější sílu, a protože nemá svůj pohyb k čemu vztáhnout, vnímá stav beztíže, jako by se pohyboval rovnoměrně a přímočaře prázdným prostorem. Z toho důvodu nemůže pozorovat žádné Unruhovo a tudíž ani Hawkingovo záření. Nic jej na horizontu nesežehne, neboť pro něho žádný horizont událostí neexistuje.
Naproti tomu Alice, pokud visí poblíž horizontu a mocným tahem svých raketových motorů brání svému pádu do černé díry, pociťuje ohromné zrychlení a pozoruje Unruhovo záření vycházející z horizontu. Podle principu ekvivalencePrincip ekvivalence – gravitační zrychlení těles nezávisí na jejich chemickém složení, gravitační a setrvačná hmotnost těles je vzájemně úměrná, ve vhodné soustavě jednotek shodná. Tento princip se někdy nazývá slabý princip ekvivalence (WEP – Weak Equivalence Principle). Podle silného principu ekvivalence by měly platit i předpoklady speciální relativity, tj. princip konstantní rychlosti světla a neodlišitelnost inerciálních soustav pro mechanické i elektromagnetické děje. Silný princip ekvivalence má za důsledek to, že by gravitační účinky měla mít i hmotnost odpovídající energii elektromagnetického pole. Důsledkem principu ekvivalence je nerozlišitelnost mezi setrvačnými a gravitačními jevy. však tomuto zrychlení můžeme rovněž říkat gravitace černé díry a pozorovanému Unruhovu záření Hawkingova radiace. Alice tedy pozoruje horizont obklopující černou díru a prostřednictvím Hawkingovy radiace může číst informace uložené na tomto horizontu, jako na obřím hologramu.
Vypařování černých děr v kvantovém prostoročase
Podle předpovědí kvantové teorie pole se s postupným vypařováním černé díry (zmenšováním rg) intenzita záření a energie emitovaných fotonů neustále zvětšuje, takže kvantová evaporace má lavinovitý charakter a závěrečné okamžiky existence černé díry završí mohutná kvantová exploze, při níž se během poslední zhruba jedné desetiny sekundy uvolní energie odpovídající současné explozi několika milionů vodíkových pum. V samém závěru svého života by pak černá díra emitovala poslední dvojici fotonů o Planckově energii Eγ = Mh c2, což představuje veškerou zbylou energii.
Podle předpovědí teorií s diskrétní metrikouMetrika – matematická struktura zobecňující pojem vzdálenosti dvou bodů. Definuje nejkratší vzdálenost mezi dvěma body v obecném (tzv. metrickém) prostoru. Tvoří-li metrický prostor například povrch koule, potom nejkratší spojnicí mezi libovolnými dvěma body tohoto prostoru je část kružnice (oblouk). Metrickým prostorem je i zakřivený prostoročas obecné relativity, a metrikou tohoto prostoru pak rozumíme nejkratší prostoročasový interval mezi dvěma událostmi v tomto prostoročase. však existuje spodní limit pro hmotnost černé díry. Je-li partonů ještě méně, vyplňují již větší prostor, než je jejich gravitační objem. Pokud uvážíme, že černá díra pojme dokonce jen tolik bitů informace, kolik se jich vejde na její povrch, dospíváme k závěru, že původní hvězda při svém hroucení pod horizont nekončí jako fyzikální singularita, ale zkolabuje do sféry o určité mezní hustotě. Když se černá díra vypařuje, její hmotnost klesá a s ní i poloměr sféry o mezní hustotě. Při poklesu hmotnosti černé díry na cca 1013 kg, se poloměr sféry vyrovná jejímu gravitačnímu poloměru (cca 10−14 m). Do té doby byl gravitační poloměr vždy větší, takže celá sféra byla zakryta horizontem. Nyní se však sféra obnaží a okamžitě „odpaří“. Průběh této exploze bude pro vzdálené pozorovatele zpomalen v důsledku gravitační dilatace času způsobené extrémně hustým kompaktním objektem. Carlo Rovelli z Univerzity Aix Marseille a Univerzity v Toulonu společně s Francescou Vidotto z Radboudovy univerzity v Nijmegenu v roce 2014 nazvali takovýto objekt Planckovou hvězdou. Pozoruhodné je, že energie emitovaná Planckouvou hvězdou je nezávislá na tom, jakých rozměrů kdysi dorostla původní černá díra. Vypařování Planckových hvězd by proto mělo být ve vesmíru jasně rozpoznatelné, ačkoliv je vyzařovaný výkon relativně malý.

Francesca Vidotto (*1982)
V kvantovaném prostoročase se tak z principu nemohou vyskytovat fyzikální singularity. V moderní fyzice je potřeba singularity prostoročasu, stejně jako bodové částice a jiná patologická monstra předpovídaná obecnou relativitou a kvantovou teorií pole, nahradit planckovskými objekty, jako jsou Planckovy hvězdy či partony. Tedy objekty konečných rozměrů a konečné hustoty.
Carlo Rovelli se svými spolupracovníky z centra pro teoretickou fyziku v Marseille před nedávnem dokázali, že smyčková kvantová gravitace generuje v nízkoenergetické limitě newtonovskou gravitaci. Na rozdíl od Newtonovy teorie však tato teorie generuje rovněž i gravitony. Výpočty ve vysokoenergetické limitě pak potvrzují, že černé díry skutečně neobsahují žádné prostoročasové singularity.
V roce 2006 objevila Fotini Makropoulou nový přístup k problému, jak vytvořit klasickou geometrii z fundamentálnější kvantové teorie. Její myšlenka vychází z představy, že částice musejí být jistým druhem emergentních excitací kvantové geometrie, které se šíří podobně, jako vlny v pevném či tekutém prostředí. Za běžných okolností se při interakci částic s okolím rozmazává informace o jejich kvantovém stavu. Tomuto jevu, známému jako dekoherence, je velmi obtížné zabránit, což velmi dobře znají konstruktéři kvantových počítačů, jejichž funkčnost spočívá právě v udržení čistých kvantových stavů, ačkoli jsou v kontaktu s okolím. Makropoulou zjistila, že obdobné postupy je možné aplikovat i na problematiku vynořování částic z dynamického kvantovaného prostoročasu.
Problém zprvu vypadal obtížně, neboť kvantové geometrie předpovídané mřížkovou kvantovou gravitací jsou velmi komplikované. Stavy částic odpovídají uzlovým grafům ve třírozměrném prostoru, který vyjma topologie nemá žádnou pevnou geometrii – ta se odvozuje teprve na základě uvedených uzlových grafů. Teorie obsahuje spoustu dodatečných proměnných, které na první pohled s geometrií přímo nesouvisejí. Důvodem je, že hrany spojující různé vrcholy grafu, se v třírozměrném prostoru mohou proplétat, uzlit a propojovat bezpočtem různých způsobů. Na jaře 2005 publikoval australský fyzik Sundance O. Bilson-Thompson článek popisující proplétání smyček, které odrážejí strukturu preonového modelu částic, o němž jsme hovořili v části Nedělitelná zrnka látky. V tomto smyčkovém pojetí je preon chápán jako páska a různé druhy preonů odpovídají různým jejím přetočením. Pásky můžeme do sebe zaplést mnoha různými způsoby, jež odpovídají všem základním částicím standardního modelu – šesti druhům kvarků a šesti druhům leptonů.

Sundance Osland Bilson-Thompson (*1979).
Zdroj: Science,
Technology & Future, YT.
Různé způsoby zaplétání a propojování hran grafu kvantového prostoročasu odpovídají různým druhům elementárních částic. To je přesně ten kousek skládačky, která Stephenu Hawkingovi chyběla, neboť uvažoval spojitý prostoročas obecné teorie relativity. Hawking zcela nenaplnil Einsteinovu vizi, protože se kvantově zabýval pouze hmotou a energií. V kvantové geometrii je však také horizont událostí černé díry kvantován. Můžeme si jej představit jako povrch složený z elementárních buněk – nul a jedniček. Každá tato nepatrná buňka odpovídá „vláknu“ spinové sítě, které protíná horizont událostí. V případě černé díry o hmotnosti Slunce existuje 1077 takových vláken, a proto 1077 různých kvantových stavů, které představují ohromnou entropii černé díry. Zvláštní lokální charakteristiky této spinové sítě horizont událostí definují. Když se černá díra kvantově vypařuje, tyto buňky se postupně „vypínají“. Při Hawkingově radiaci se kvanta horizontu černé díry přeměňují na kvanta energie ~ hmoty a oddělují od horizontu.
Podle indického teoretického fyzika Abhay Ashtekara jde přesně o naplnění Einsteinovy představy, podle níž geometrie má fyzikální význam. Dokonce se přeměňuje v hmotu. Tento proces neprobíhá spojitě, ale v celistvých krocích, protože je kvantován. Černá díra se proto nesmršťuje spojitě, ale chová se spíše jako excitovaný atom, který ztrácí energii po kvantech.
* * *
Všechny bulletiny této série
- Kvantování prostoročasu – fyzika v nesnázích
- Kvantování prostoročasu – nedělitelná zrnka látky
- Kvantování prostoročasu – holografický vesmír
- Kvantování prostoročasu – entropická gravitace
- Kvantování prostoročasu – multiverzum
- Kvantování prostoročasu – paralelní světy
- Kvantování prostoročasu – strašidelné působení na dálku
- Kvantování prostoročasu – privilegovaný systém – návrat ztraceného syna
Odkazy
- Vojtěch Ullmann: Gravitace, černé díry a fyzika prostoročasu; Čas, 1986
- Luboš Motl: Holografický princip; Vesmír, 1998
- Lee Smolin: Fyzika v potížích; Argo, 2009
- Leonard Suskind: Válka o černé díry; Argo, 2013
- Lee Smolin: Znovuzrozený čas; Argo, 2015
- Stanislav Mihulka: Astrofyzikální přestřelka s ohnivou zdí a Planckovými hvězdami; Osel, 17. února 2014
