Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. Vydavatel: AGA (Aldebaran Group for Astrophysics) Číslo 34 – vyšlo 30. srpna, ročník 17 (2019) © Copyright Aldebaran Group for Astrophysics Publikování nebo šíření obsahu je zakázáno. ISSN: 1214-1674, Email: bulletin@aldebaran.cz

34/2019

Mapa gravitačních teorií

Rudolf Mentzl

Gravitace je bezpochyby nejdéle zkoumaná základní síla. Přestože její projevy dokážeme správně spočítat s přesností daleko převyšující naše reálné potřeby, stále tápeme, jak ji správně uchopit. Víme totiž, že naše teorie nejsou správné. Obecná teorie relativityObecná relativita – teorie gravitace publikovaná Albertem Einsteinem v roce 1915. Její základní myšlenkou je tvrzení, že každé těleso svou přítomností zakřivuje prostor a čas ve svém okolí. Ostatní tělesa se v tomto pokřiveném světě pohybují po nejrovnějších možných drahách, tzv. geodetikách., která je tak úspěšná při popisu působení gravitace na velkých vzdálenostech, je ve sporu s kvantovou teoriíKvantová teorie pole – popis interakce založený na kvantových principech, tj. na nekomutativnosti základních operací v mikrosvětě. Kvantová teorie pole nahrazuje silové působení polními částicemi. Tyto částice jsou virtuální a nikdy nemohou skončit v detektoru, působí jen mezi dvěma interagujícími částicemi. Jako první prototyp kvantové teorie pole se vyvinula ve 30. letech 20. století kvantová elektrodynamika, později se objevila teorie slabé a silné interakce. Jediná gravitace je popsána jinak – za pomoci obecné relativity., která popisuje svět neméně přesně, ale na malých měřítcích. Tam, kde se tyto dvě teorie potkají, předvídají nekonečné hodnoty, což je neklamný znak jejich selhání. Již mnoho desetiletí fyzici doufají, že naleznou jednotnou teorii popisující vesmír jediným způsobem. Pokud taková teorie vůbec existuje, musí obecnou relativitu i kvantovou teorii obsahovat jako dva okrajové případy, podobně jako obecná relativita obsahuje Newtonův gravitační zákon. V tomto článku představíme některé z hlavních směrů, kudy se výzkum ubírá.

Isaac Newton byl zakladatelem moderního pojetí vědy a autorem
první úspěšné teorie gravitace. Zdroj: My Face.

Obecná relativita – teorie gravitace publikovaná Albertem Einsteinem v roce 1915. Její základní myšlenkou je tvrzení, že každé těleso svou přítomností zakřivuje prostor a čas ve svém okolí. Ostatní tělesa se v tomto pokřiveném světě pohybují po nejrovnějších možných drahách, tzv. geodetikách. Kvantová gravitace – teorie pokoušející se spojit zákony kvantové mechaniky se současnou teorií gravitace, obecnou relativitou. Zdá se, že nejblíže cíli jsou tzv. teorie strun. Smyčková gravitace – Loop Quantum Gravity, teorie snažící se rozpor mezi obecnou relativitou a kvantovou teorií vyřešit kvantováním prostoru na základní kvanta – tzv. smyčky. Síť těchto smyček se nazývá spinová pěna. Rozměry smyček by měly být rovny Planckově délce, tj. 10−35 m. Kvadratická gravitace – třída alternativních teorií gravitace, které rozšiřují rovnice obecné relativity o druhou mocninu Ricciho skaláru (popisuje skalární křivost, v OTR je v první mocnině) a zúžení Weylova tenzoru (popisuje torzní a slapové jevy, OTR ho neobsahuje) se sebou samým. Jsou-li tyto členy rovny nule, přechází rovnice kvadratické gravitace v klasickou Einsteinovu obecnou teorii relativity (OTR).

Jak to začalo

První teorii gravitace, podpořenou matematickým aparátem, přivedl na svět Isaac Newton. Je to jednoduchý vztah, který popisuje, že gravitační síla ubývá s druhou mocninou vzdálenosti. Druhá mocnina souvisí s geometrií našeho prostoru. Dlouho se zdálo, že je vzorec dokonalý, ale přesná pozorování poukazovala na drobné chyby. Nejznámější případ je stáčení perihéliaPericentrum – bod na eliptické dráze kolem centrálního tělesa, který je tomuto tělesu nejblíže. Pro Slunce se používá výraz perihélium, pro Zemi perigeum, pro Měsíc periluna, pro Jupiter perijovum, pro Saturn perikronum, pro Mars periareion a pro hvězdu periastrum. oběžné dráhy MerkuruMerkur – planeta nejbližší Slunci. Je to skalnatá planeta, posetá krátery podobně jako náš Měsíc. Jde o nejmenší planetu vůbec. Je téměř bez atmosféry. Teplota povrchu tohoto tělesa kolísá mezi −180 °C a 430 °C. Merkur se otočí kolem vlastní osy jednou za 59 našich dní. Jeho doba oběhu kolem Slunce trvá 88 dní. Jde o příklad vázané rotace (spinorbitální interakce) v poměru 2:3 způsobené slapovými silami. Dráha Merkuru kolem Slunce je protáhlá elipsa, která se stáčí vlivem přítomnosti ostatních planet. Malá část stáčení perihelia dráhy (43″ za století) je způsobena efekty obecné relativity. (i po odečtení známých poruch od ostatních planet). Za pozornost stojí jeden ze způsobů vysvětlení, který upravoval Newtonův zákon. Předpokládal, že číslo v exponentu vzdálenosti není přesně 2, ale má hodnotu jen o málo menší. Pak by vzorec předpovídal dráhu Merkuru tak, jak byla pozorována. Z dnešního pohledu je tento pokus úsměvný, nicméně, když se na něj podíváme tak, jak by asi sám autor nečekal, mohli bychom usoudit, že geometrie prostoru v místech Merkuru není eukleidovská, že povrch koule není 4πr², což by odpovídalo dnešnímu pojetí gravitace – obecné teorii relativity.

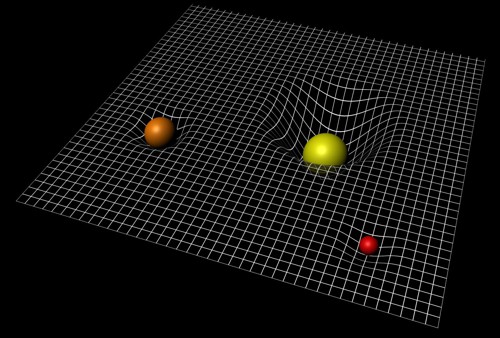
Každé těleso kolem sebe zakřivuje a spoluvytváří jemné předivo času a prostoru.
Zdroj: ESA.

Obecná teorie relativity pojem síly vůbec nezavádí. V Einsteinově pojetí zakřivují tělesa čas a prostor svou hmotností a vše se v něm pohybuje po nejpřímějších možných drahách, tzv. geodetikáchGeodetika – nejrovnější možná dráha v zakřiveném časoprostoru. Po této dráze se pohybují všechna volná hmotná tělesa bez rozdílu.. O tomto principu již bylo napsáno mnoho textu, podrobnosti například v sekci Astrofyzika. V současnosti se jedná o nejprecizněji propracovanou, obecně uznávanou, teorii gravitace, která zatím přesně vysvětlila všechny pozorované jevy. Na velmi malých škálách, jejichž zkoumání je zatím mimo naše technické možnosti, však dává znepokojující předpovědi. Je několik cest, kudy z toho ven.

Posviťme si na malé škály

Pokusy o sjednocení obecné relativity a kvantové teorie selhávají, když se přiblížíme k tzv. Planckovým škálámPlanckovy škály – charakteristické rozměry získané kombinací fundamentálních konstant (gravitační, Planckovy a rychlosti světla). Planckova délka vychází 10⁻³⁵ m, Planckův čas 10⁻⁴³ s, Planckova hmotnost 10⁻⁸ kg a Planckova energie 10¹⁹ GeV.. V praktickém životě nás to neomezuje, protože jde o rozměry o pětadvacet řádů menší, než je průměr atomuAtom – základní strukturní jednotka hmoty, jádro je složeno z neutronů a protonů, obaly z elektronů. Rozměry atomu jsou 10⁻¹⁰ m, rozměry jádra 10⁻¹⁴ m, hustota atomu je 10¹¹ g·cm⁻³, hustota jádra 10¹⁴ g·cm⁻³. Elektrony nejsou v atomárnáím obalu lokalizovány, můžeme určit jen pravděpodobnosti jejich výskytu v tzv. orbitalech.. Logickým krokem, jak se z tohoto problému dostat, je hledat mechanizmy, které zabrání jít do takto malých rozměrů. Můžeme třeba přijmout premisu, že elementární částice nejsou bodové, ale mají nějakou minimální velikost. Tímto směrem se ubírá teorie strunStruny – jednodimenzionální útvary ve vícerozměrném světě (uzavřené nebo otevřené), jejichž vibrační stavy odpovídají jednotlivým elementárním částicím. Jde o podstatný prvek tzv. strunových teorií, které se pokoušejí spojit svět kvantové teorie se zakřiveným prostoročasem obecné relativity., později teorie superstrunSuperstruny – jednodimenzionální útvary charakterizující elementární částice v teorii strun. Předpona super znamená, že je do teorie zahrnuta tzv. supersymetrie, tj. každá částice existuje ve dvou provedeních – jako boson i jako fermion.. Předpokládá, že všechny dosud známé částice jsou tvořeny jakýmisi základními kameny – strunami. Název pramení z toho, že by tyto struktury měly mít tvar jednorozměrných strun navzájem se lišících vibračními stavy. Teorie ještě navíc vyžaduje další prostorové rozměry. To se může zdát podezřelé, protože naše denní zkušenost počítá jen se čtyřmi, započítáme-li i čas. Je však možné, že na mikroskopické úrovni můžeme, až se zdokonalí naše pozorovací technika, narazit na další, tzv. svinuté dimenze. Asi jako se nám vlas zdá být jednorozměrný, ale pod mikroskopem uvidíme, že jeho povrch má nejen délku, ale i příčný směr, který vlas obtáčí v uzavřené smyčce. Je dechberoucí, že tímto jednoduchým principem lze zkonstruovat všechny známé elementární částice, tedy i ty, které zprostředkovávají interakce. Jedna z těchto částic má vlastnosti, jaké očekáváme u hypotetického gravitonuGraviton – hypotetická polní částice gravitační interakce, která by měla smysl, pokud by gravitace byla popsatelná kvantovou teorií. Graviton by měl mít spin 2. Našimi současnými prostředky není detekovatelný..

Název teorie strun se drží už jen z historických důvodů, protože struny sehrály klíčovou roli u jejího vzniku. Dnes tu ovšem vystupují i další objekty, jako například membrány, zkráceně brány. Českou stopu zde zanechal strunový fyzik Petr Hořava, když v roce 1989 objevil tzv. D-brány. To jsou plochy v časoprostoru, kde mohou končit struny. Matematicky jsou omezeny Dirichletovými okrajovými podmínkamiOkrajové podmínky – podmínky zajišťující jednoznačnost řešení parciálních diferenciálních rovnic. Dirichletovy podmínky předepisují hodnotu hledané funkce na hranici výpočetní oblasti. Neumannovy podmínky předepisují hodnotu první derivace hledané funkce na hranici výpočetní oblasti., proto je v názvu písmeno D. Pojmenování D-brány vzniklo na popud amerického fyzika Josepha Polchinského, kterému je i neprávem přičítáno prvenství Hořavova objevu. Ten sehrál v roce 1995 zásadní roli při vzniku M-teorieM-teorie – teorie superstrun zastřešující jednotlivé dosavadní teorie strun, které jsou její nízkoenergetickou limitou. Jednotný pohled na různé teorie strun je dosažen přidáním páté makroskopické dimenze (tzv. Kaluzovy-Kleinovy dimenze) ke čtyřem časoprostorovým a několika svinutým dimenzím (zpravidla 6 nebo 22)..

Teorie superstrun se později rozvinula do pěti teorií, které jedinečným způsobem problém popisovaly. To je samozřejmě podezřelé, ale později se ukázalo, že tyto teorie nejsou nezávislé, jak to z počátku vypadalo. Jejich syntézou vznikla tzv. M-teorieM-teorie – teorie superstrun zastřešující jednotlivé dosavadní teorie strun, které jsou její nízkoenergetickou limitou. Jednotný pohled na různé teorie strun je dosažen přidáním páté makroskopické dimenze (tzv. Kaluzovy-Kleinovy dimenze) ke čtyřem časoprostorovým a několika svinutým dimenzím (zpravidla 6 nebo 22).. Zvláštním bonusem strunového přístupu je také vysvětlení, proč je gravitační síla v porovnání s jinými tak slabá. Vícerozměrný prostor by umožňoval únik gravitačního působení do jiných (makroskopických) dimenzí. Odpůrci M-teorie ji sice přiznávají vnitřní eleganci a principiální jednoduchost, ale jedním dechem vytýkají neúměrnou matematickou složitost. Přes veškerý pokrok v matematice se leckdy nedaří sestavit ani samotné rovnice popisující problém. Teorie také předpovídá existenci částic a extradimenzí, které zatím nikdo nepozoroval. Prubířským kamenem by samozřejmě byl experiment, který by rozhodl ve prospěch klasických teorií nebo M-teorie. Takový však zatím nemáme.

Umělecká podoba Feynmanových diagramů strun. Kresba Ivan Havlíček.

Jiný způsob, jak se vyhnout příliš malým rozměrům, je přijmout premisu, že sám prostor není spojitý, ale je složený z jakýchsi kvant prostoru nazývaných smyčky. To je základní koncept tzv. smyčkové gravitaceSmyčková gravitace – Loop Quantum Gravity, teorie snažící se rozpor mezi obecnou relativitou a kvantovou teorií vyřešit kvantováním prostoru na základní kvanta – tzv. smyčky. Síť těchto smyček se nazývá spinová pěna. Rozměry smyček by měly být rovny Planckově délce, tj. 10⁻³⁵ m.. Smyčky spolu navzájem komunikují, vytvářejí předivo prostoru nazývané spinová pěna. Z této koncepce se vytrácí pojem prostoru i času. Prostor je tvořen provázáním jednotlivých smyček a představa makroskopického plynutí času vzniká v důsledku vztahů mezi jednotlivými kvanty prostoru.

Ačkoli myšlenka smyčkové gravitace není dosud opuštěna, potýká se se závažnými problémy. Prostor rozdrobený na smyčky by měl mít vlastnost, kterou v makroskopickém ekvivalentu pojmenováváme index lomuIndex lomu – absolutní index lomu je v homogenním izotropním prostředí bez disperze definován jako podíl rychlosti světla a fázové rychlosti. Obecně je index lomu komplexní veličina závislá na frekvenci, v případě anizotropního prostředí tenzorová. Frekvenční závislost reálné části popisuje disperzi v daném prostředí. Imaginární část indexu lomu popisuje (v závislosti na znaménku) absorpci nebo zesílení světla. Relativní index lomu je dán poměrem indexů lomu prostředí, do kterého záření vstupuje vůči indexu lomu prostředí, z něhož záření vychází. Na rozhraní dvou prostředí je relativní index lomu roven podílu sinu úhlu dopadu a sinu úhlu lomu (Snellův zákon). Uvozující přídavné jméno (absolutní nebo relativní) se často vypouští, takže zda se jedná o absolutní či relativní index lomu poznáme pouze z kontextu.. Signál šířící se prostorem by se měl zpomalovat přeskoky od jedné smyčky k druhé, v závislosti na jeho energii. Jinými slovy, rychlost světla by měla být závislá na vlnové délce. Zatím se tuto disperzi nejen nepodařilo pozorovat, ale z analýzy světla, které k nám přilétá z končin vesmíru vzdálených miliardy světelných rokůSvětelný rok – ly (light year), vzdálenost, kterou světlo ve vakuu urazí za jeden rok, ly = 9,46×10¹² km. Menšími jednotkami jsou: světelný den, světelná hodina, světelná minuta a světelná sekunda. Větší jednotkou je 1000 ly, což označujeme zkratkou kly. Tyto jednotky se velmi často používají v populárních textech. V odborných textech se spíše využívají parseky. (tady by měla být disperze již dobře patrná), vysvítá, že pokud je snad prostor kvantován, rozměr zrn je možná ještě menší, než je Planckova délka.

Umělecká představa prostoru tvořeného spinovou pěnou.
Zdroj: Carlo Rovelli, Francesca Vidotto.

Opravme Einsteina

Pozapomeňme na problémy s kvantováním a podívejme se, zda je správně obecná relativita (OTR). To je výzva poměrně smělá, protože jsme zatím nenašli sebemenší odchylky předpovědí OTR od pozorovaných jevů. Nová teorie gravitace by tedy měla OTR zahrnovat jako svou limitní formu. Mezi takové alternativní teorie patří i rozsáhlá třída teorií nazývaná kvadratické gravitace. Obecná teorie relativity je závislá na hodnotách dvou základních konstant. Na gravitační a na kosmologické konstantě. Kvadratické gravitace přibírají ještě další dva členy, které se zde vyskytují ve své druhé mocnině. To je také důvod, proč se mluví o kvadratických gravitacích.

V souvislosti s kvadratickými gravitacemi připomeňme nedávný průlom ve zobecnění Schwarzschildova řešení nerotující černé díryČerná díra – objekt, který kolem sebe zakřiví čas a prostor natolik, že z něho nemůže uniknout ani světlo. Část z nich vzniká kolapsem hvězdy v zá­vě­reč­ných fázích vývoje. Druhou skupinu tvoří obří černé díry sídlící v centrech galaxií. Rotující černé díry kolem sebe vytvářejí akreční disky látky a v ose rotace výtrysky vysoce urychlených částic. Paradoxně akreční disky i výtrysky, vznikající v bezprostředním okolí černé díry, velmi intenzivně vyzařují., tentokrát pomocí kvadratické gravitace. Za úspěchem stojí (v abecedním pořadí) Jiří Podolský (MFF UK), Vojtěch Pravda, Alena Pravdová (oba MÚ AV ČR) a Robert Švarc (MFF UK). Zatímco je Schwarzschildovo řešení pomocí OTR poměrně jednoduché, kvadratické gravitace neměly donedávna jinou možnost, než se odvolat na numerické metody se všemi problémy, které přinášejí. Výše zmíněnému týmu se podařilo najít explicitní tvar metriky, který problém popisuje. Mimo jiné tím ukázali, že v kvadratické gravitaci neplatí tzv. Birkhoffův teorém. Birkhoffův teorém tvrdí, že Schwarzschildovo řešení je v OTR jediné možné. Podle kvadratických gravitací je třída řešení širší. Analytické řešení rovnic gravitačního pole se opírá o tzv. Bachův tenzorBachův tenzor – jeden z tenzorů popisujících zakřivení časoprostoru, který poprvé použil německý fyzik Rudolf Bach v roce 1921. Je kombinací Weylova tenzoru a Schoutenova tenzoru. Má nulovou stopu a ve čtyřech dimenzích je konformně invariantní.. Při jeho nulové hodnotě přechází rovnice v klasické Schwarzschildovo řešení. Mluvíme o Schwarzschildově-Bachově černé díře, zkráceně o díře Schwa-Bach.

Svou stopu na poli alternativních teorií gravitace zanechal i původně strunový fyzik Petr Hořava. Mezinárodní pozornost přitáhl teorií nazývanou Hořavova-Lifšicova. Sama teorie je pouze Hořavovo dílo, protože však k jejímu rozvinutí použil matematické postupy ruského fyzika Jevgenije M. Lifšice (1915–1985), figuruje v názvu i druhé jméno. Základní princip budí pochybnosti, protože se tváří jako velký krok zpět. Teorie ustupuje od rovnocennosti prostorové a časové souřadnice, takže není invariantní vůči Lorentzovým transformacím. Je zřejmé, že jakkoli zhoubně se teorie tváří vůči mnohokrát ověřeným pozorováním na makroskopických vzdálenostech a malých energiích, v mikrosvětě odstraní problémy s divergencemi veličin, jako jsou hmotnost a energie. P. Hořava našel v roce 2009 způsob, jak se s fatálním nedostatkem vypořádat. Formuloval teorii, podle které se ve světě vysokých energií invariance vůči Lorentzovým transformacím nezachovává, ale v limitě nízkých energií ano. Některé symetrie, které Einstein postuloval jako výchozí, zde vyplynou z podstaty věci, což teorii přidává na zajímavosti.

A co když gravitace neexistuje?

Všechny dosud uvedené teorie se snaží pouze o popis, jak gravitace působí, žádná se nepokouší odpovědět na otázku proč. Víme, že je mikrosvět kvantován, ale už neřešíme proč. Víme, jakým způsobem hmotnost zakřivuje prostoročas, nevíme však, proč to tak dělá. Na tom není nic znepokojujícího, přírodní vědy si odpovědi na otázku proč rezervují pro problémy, které nejsou základní. Pokud by gravitace základní silou nebyla, mohli bychom se pokusit odpovědět, proč tu je, a tím by odpadl i rozpor s kvantovou teorií. Co gravitaci způsobuje, se lidé pokoušeli vysvětlit již dávno. Byla tu jakási naivní představa, že je prostor vyplněn mikroskopickými částicemi, které termickým pohybem tlačí na tělesa, podobně jako molekuly vzduchu tlačí na vše kolem nás. Osamělé těleso by tyto částice bombardovaly souměrně ze všech stran, jejich celkový účinek by byl tedy nulový. Dvě planety vedle sebe by se však navzájem poněkud stínily, proto by byl vnější tlak větší a tělesa by se přitahovala. Z tohoto principu doplněného těžko stravitelnými ad hoc podmínkami vysvítala i kvadratická závislost síly na převrácené hodnotě vzdálenosti. Je však zřejmé, že takové částice by musely vytvářet odporující prostředí a planety by se na svých drahách zpomalovaly. Rozporů s realitou je mnohem více, proto si dnes z tohoto přístupu ponechme pouze myšlenku, že gravitace nemusí být základní silou. Velký pokrok v takovém bádání v posledních letech přinesl holandský fyzik Erik Verlinde.

Erik Verlinde. Fotografie: Bob Bronshof.

O Verlindeho přístupu k řešení problému gravitace jsme již několikrát informovali: AB 46/2011, AB 22/2018 a AB 18/2019, proto princip nastíníme jen ve vší stručnosti. Podle Verlindeho gravitace ve skutečnosti neexistuje, to, co pozorujeme, je jen statistickým projevem mikroskopických procesů. Verlinde chápe gravitaci jako entropickou sílu, která vzniká při nárůstu entropieEntropie – v termodynamice je definována vztahem dS = dQ/T, kde dQ je diferenciál tepla a T je absolutní teplota (1/T je integrační faktor). Takto zavedená entropie je na rozdíl od tepla úplným diferenciálem, její integrál nezávisí na cestě ve stavovém prostoru. Ve statistice má entropie význam logaritmické míry pravděpodobnosti realizace stavu, v kvantové teorii je logaritmickou mírou počtu kvantových stavů, kterými lze daný makroskopický stav realizovat. Entropie tak souvisí s „množstvím chaosu“ v systému. V informatice entropie popisuje množství informací. V uzavřeném systému může entropie jen růst. V termodynamické rovnováze dosáhne svého maxima.. Sama entropie má plošné zdroje (holografický princip) a objemové zdroje (kvantové fluktuace). V první verzi v roce 2011 mu z jeho analýz jako vedlejší produkt vypadl Newtonův gravitační zákon, což je samo o sobě pozoruhodné. O několik let později takto získal i OTR a v některých speciálních případech dokáže i vysvětlit projevy, které se připisují temné hmotě a energii. Jakkoli je tato teorie přitažlivá, není zatím ověřena.

Která teorie je nejlepší?

Pokusili jsme se zmapovat alternativní teorie gravitace, výčet zřejmě není úplný. Vynechali jsme exotické teorie předpokládající imaginární hmotnost, nezmínili jsme ani MONDMOND – Modified Newtonian Dynamics, úpravy Newtonových zákonů, které měly za cíl vysvětlit rozdělení rychlostí hvězd v galaxiích jinak než za pomoci temné hmoty. – modifikovanou newtonowskou dynamiku, která se snaží úpravou gravitačního zákona odstranit potřebu temné hmoty v galaxiích. Pozorování chování slupkových galaxiíSlupková galaxie – eliptická galaxie obklopená slupkou hvězd, nikoli jen prstencem. Poprvé takové galaxie detekoval australský astronom a vynikající fotograf David Malin v roce 1979. a srovnání výsledků s numerickými simulacemi dává nadějné výsledky. Je snad tedy MOND ta správná teorie?

Jediným kritériem správnosti teorie je shoda s realitou, tedy srovnávání s již známými fakty a experimentem. Dokud teorie tuto shodu neporušují, není možné rozlišit, která z nich je ta správná. Fyzika nehledá věčné pravdy, nýbrž matematické modely reality. To však neznamená, že by se fyzikové do filozofických otázek nesměli pouštět, nechat se jimi vést a případně je včas opustit, pokud je dovedou do míst, kde se názor rozchází s pozorováním. Teorie poskytující stejné výsledky pak hodnotí podle jejich vnitřní elegance a svého osobního vztahu, což je samozřejmě subjektivní pohled. Správným krokem je navrhnout experiment, který rozhodne. Na sjednocení obecné relativity a kvantové teorie pracují nejlepší mozky již od počátku minulého století, přesto se dosud nepodařilo problém uspokojivě rozřešit. Možná se ještě ten správný mozek nenašel, možná jednotná teorie neexistuje. To už jsme ale za hranicemi fyziky. Řečeno s Cimrmanem: vyrovnat se s tím, toť věčný úděl filozofie.

Odkazy