Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. Vydavatel: AGA (Aldebaran Group for Astrophysics) Číslo 18 – vyšlo 3. května, ročník 17 (2019) © Copyright Aldebaran Group for Astrophysics Publikování nebo šíření obsahu je zakázáno. ISSN: 1214-1674, Email: bulletin@aldebaran.cz

18/2019

Zvítězí Verlinde nad temnotou?

Petr Kulhánek

Mezi lety 2009 až 2011 šokoval Erik Verlinde, holandský teoretik působící tehdy v Princetonu, svět svým názorem, že gravitace nepatří k základním interakcím, ale je způsobena statistickými projevy mikrosvěta a je tedy ve skutečnosti pouze maskovanou kvantovou interakcí. Od té doby už uplynulo hodně vody. Verlinde svou první verzi teorie doplnil v roce 2016 o další postulát, jehož výsledkem je, že jeho teorie nedává stejné výsledky jako Newtonův gravitační zákon či obecná relativitaObecná relativita – teorie gravitace publikovaná Albertem Einsteinem v roce 1915. Její základní myšlenkou je tvrzení, že každé těleso svou přítomností zakřivuje prostor a čas ve svém okolí. Ostatní tělesa se v tomto pokřiveném světě pohybují po nejrovnějších možných drahách, tzv. geodetikách.. V prostředí s vysokou hustotou látky, například ve Sluneční soustavě, splývají předpovědi s Keplerovými zákony nebo v extrémních situacích s obecnou relativitou. Při nízké hustotě látky, například u celé galaxie či u kupy galaxií, jsou ale předpovědi odlišné. A to už začíná být zajímavé. Pokud dvě teorie dávají různé výsledky, může jen experiment rozhodnout, která z nich je v souladu s přírodními jevy, jež chceme popsat. Za poslední dva roky se objevila zhruba pětice prací, která se o to pokouší. Jak už to u nových teorií bývá, zatím jsou výsledky rozporuplné, některé práce teorii potvrzují, jiné vyvracejí. Nejzajímavější ale je, že poslední varianta Verlindovy teorie nepotřebuje k popisu rotačních křivek galaxií temnou hmotu, což by mohlo znamenat velký názorový posun při interpretaci stávajících měření. Pojďme se v dnešním bulletinu na tyto záležitosti podívat podrobněji.

Fluktuace vakua jsou objemovým zdrojem entropie, který způsobuje
odchylky Verlindovy teorie od obecné relativity. Zdroj: Narinder.

Obecná relativita – teorie gravitace publikovaná Albertem Einsteinem v roce 1915. Její základní myšlenkou je tvrzení, že každé těleso svou přítomností zakřivuje prostor a čas ve svém okolí. Ostatní tělesa se v tomto pokřiveném světě pohybují po nejrovnějších možných drahách, tzv. geodetikách. Kvantová teorie pole – popis interakce založený na kvantových principech, tj. na nekomutativnosti základních operací v mikrosvětě. Kvantová teorie pole nahrazuje silové působení polními částicemi. Tyto částice jsou virtuální a nikdy nemohou skončit v detektoru, působí jen mezi dvěma interagujícími částicemi. Jako první prototyp kvantové teorie pole se vyvinula ve 30. letech 20. století kvantová elektrodynamika, později se objevila teorie slabé a silné interakce. Jediná gravitace je popsána jinak – za pomoci obecné relativity. Entropie – v termodynamice je definována vztahem dS = dQ/T, kde dQ je diferenciál tepla a T je absolutní teplota (1/T je integrační faktor). Takto zavedená entropie je na rozdíl od tepla úplným diferenciálem, její integrál nezávisí na cestě ve stavovém prostoru. Ve statistice má entropie význam logaritmické míry pravděpodobnosti realizace stavu, v kvantové teorii je logaritmickou mírou počtu kvantových stavů, kterými lze daný makroskopický stav realizovat. Entropie tak souvisí s „množstvím chaosu“ v systému. V informatice entropie popisuje množství informací. V uzavřeném systému může entropie jen růst. V termodynamické rovnováze dosáhne svého maxima. Temná hmota – hmota ve vesmíru nebaryonové povahy, která není složena z kvarků. Temná hmota udržuje pohromadě svítící objekty velkých rozměrů, které díky ní v periferních oblastech obíhají rychleji, než odpovídá gravitačnímu zákonu aplikovanému na viditelnou hmotu. Podle posledních odhadů na základě pozorování existuje ve vesmíru 5 % baryonové hmoty, 27 % temné hmoty a 68 % temné energie. Existuje několik hypotetických částic, které jsou vhodnými kandidáty na částice temné hmoty, dosud však nebyly objeveny. Termín „temná hmota“ zavedl v roce 1933 Fritz Zwicky, když zjistil, že se členové Kupy galaxií ve Vlasech Bereniky pohybují v průměru rychleji, než by odpovídalo gravitačním účinkům viditelné látky. Existují také teorie, které se pokoušejí vysvětlit rotační křivky galaxií a pohyby galaxií v kupách jiným způsobem než temnou hmotou. Temná energie – entita zodpovědná za zrychlenou expanzi vesmíru, která byla objevena na konci roku 1998 (Saul Perlmutter, Adam Riess). Temná energie tvoří 68 % hmoty a energie ve vesmíru. Hustota temné energie je velmi málo proměnná v čase i v prostoru, pokud vůbec. Nejnadějnějším kandidátem na temnou energii je energie vakuových fluktuací.

Jak šel čas

Kořeny vztahu mezi termodynamikou, statistikou a gravitací sahají až do roku 1973. Tehdy izraelský teoretik Jacob Beckenstein (*1947) zjednodušeně analyzoval myšlenkový experiment, při němž periodicky házel do černé díryČerná díra – objekt, který kolem sebe zakřiví čas a prostor natolik, že z něho nemůže uniknout ani světlo. Část z nich vzniká kolapsem hvězdy v zá­vě­reč­ných fázích vývoje. Druhou skupinu tvoří obří černé díry sídlící v centrech galaxií. Rotující černé díry kolem sebe vytvářejí akreční disky látky a v ose rotace výtrysky vysoce urychlených částic. Paradoxně akreční disky i výtrysky, vznikající v bezprostředním okolí černé díry, velmi intenzivně vyzařují. fotony uvolňované z nějaké nádoby, která se opakovaně dostávala do blízkosti horizontu černé díry. Napadlo ho, že by takové zařízení v podstatě fungovalo jako klasický tepelný stroj. Ten ale může trvale a cyklicky fungovat jen s dvěma teplotami – teplotou kotle a teplotou chladiče. Za vyšší teplotu posloužila sama teplota fotonů. S chladičem ztotožnil Beckenstein povrch černé díry a z jednoduchých úvah odvodil, jaká by teplota povrchu černé díry jakožto chladiče měla být. Tato teplota je velmi malá, například pro černou díru o hmotnosti našeho Slunce vychází pouhých 10^-7 K. O dva roky později provedl anglický teoretik Stephen Hawking (1942–2018) mnohem preciznější výpočet na základě kvantové teorie pole. Teplota povrchu černé díry mu vyšla stejná jako Beckensteinovi a navíc předpověděl mechanizmus Hawkingova vypařování černé díry. Díky kvantovým procesům (ať už si je představíme jako tunelování z oblasti pod horizontem či jako kreaci virtuálního páru nad horizontem, při níž jedna částice skončí pod horizontem) mohou černou díru přece jen tu a tam některé částice opustit. Černá díra by měla proto zářit jako černé těleso o Beckensteinově teplotě. Tímto efektem by se černá díra o hmotnosti Slunce vypařila za neskutečných 10⁶² let (stáří vesmíru je 14 miliard let). Není jasné, zda je Hawkingův jev reálný fyzikální mechanizmus a zda bude vypařování černých děr někdy detekováno. Beckenstein i Hawking přispěli k existenci nové vědní disciplíny: termodynamice černých děr. Pokud přiřadíme povrchu černé díry teplotu, můžeme mu přiřadit i entropiiEntropie – v termodynamice je definována vztahem dS = dQ/T, kde dQ je diferenciál tepla a T je absolutní teplota (1/T je integrační faktor). Takto zavedená entropie je na rozdíl od tepla úplným diferenciálem, její integrál nezávisí na cestě ve stavovém prostoru. Ve statistice má entropie význam logaritmické míry pravděpodobnosti realizace stavu, v kvantové teorii je logaritmickou mírou počtu kvantových stavů, kterými lze daný makroskopický stav realizovat. Entropie tak souvisí s „množstvím chaosu“ v systému. V informatice entropie popisuje množství informací. V uzavřeném systému může entropie jen růst. V termodynamické rovnováze dosáhne svého maxima.. Není právě v ní zakódována informace o látce uvnitř černé díry? Každá částice, která horizontem prošla, ať už dovnitř, či naopak kvantovými procesy ven, nepatrně přispěla ke zvlnění horizontu černé díry. Právě tyto fluktuace (plošná entropie) by mohly být zdrojem informací o vnitřku černé díry. Zakódování informace na méněrozměrné množině o vícerozměrném objektu se nazývá holografický princip a zdá se, že jde o důležitý princip fungující jak v makrosvětě, tak v mikrosvětě.

Informace by měla být zakódována na nějakém nosiči, v tomto smyslu je třeba s informacemi zacházet obdobně jako s energií či hmotou. Množství informace v dané objemové jednotce musí být konečné (tzv. princip maxima entropie), nemůže mít nekonečnou hodnotu podobně jako množství energie či hmoty soustředěné v konečné oblasti. Výsledkem principu maxima entropie je fakt, že elementární částice nemohou být dělitelné do nekonečna. Někde musí existovat hranice tvořená skutečně elementárními, dále nedělitelnými částicemi. Možná to jsou dnešní kvarkyKvarky – částice, ze kterých jsou tvořeny těžké částice s vnitřní strukturou (hadrony). Hadrony dělíme na baryony složené ze tří kvarků (například protony a neutrony) a na mezony tvořené kvarkem a antikvarkem (například piony). Kvarky se dělí do tří generací, první tvoří kvarky „d“ (down) a „u“ (up), druhou kvarky „s“ (strange) a „c“ (charm) a třetí kvarky „b“ (bottom nebo beauty) a „t“ (top nebo truth). Kvarky mají neceločíselné (třetinové a dvoutřetinové) elektrické náboje. Jsou také nositeli barevného náboje silné interakce. a leptonyLeptony – skupina částic, mezi které patří elektron, těžký elektron (mion) a supertěžký elektron (tauon) a jejich neutrina (elektronové, mionové a tauo­nové). Tyto částice nepodléhají silné interakci, ale jen slabé a elektro­mag­ne­tické (pokud jsou nabité)., možná bude existovat ještě nějaká další úroveň dělení. Pokud se bude taková částice navenek jevit jako struktura s určitým rozměrem (například bude strunou či něčím jiným), bude muset být veškerá informace o jejím vnitřku zapsaná na povrchu tohoto útvaru. Hovoříme o tzv. projekční ploše. I v mikrosvětě by tedy mohl v nějaké podobě fungovat holografický princip. S těmito myšlenkami oživili termodynamiku mikrosvěta nizozemský teoretik Gerardus t'Hooft (*1946) a americký teoretik Leonard Susskind (*1940) v roce 1994.

Jedna z variant Beckensteinova experimentu. Kresba: Ivan Havlíček.

Informace v konečné oblasti nemůže být nekonečná. Zdroj: Thought Co.

O pouhý rok později, v roce 1995, ukázal americký teoretik Ted Jacobson (*1954) z Marylandské univerzity, že z termodynamiky a entropie lokalizované na povrchu lze odvodit Einsteinovy rovnice obecné relativity [1]. Blízkost obou disciplín byla najednou ještě těsnější. Nešlo o novou teorii, jen o zajímavé alternativní odvození, které nevede k jiným výsledkům, než dává obecná relativita předložená dříve Einsteinem. O dalších 15 let později, v roce 2010, vstupuje na scénu holandský teoretik Erik Verlinde a Jacobsonův koncept prohlubuje [2]. Gravitaci začíná vnímat jako statistické projevy mikrosvěta. Koncept entropie chápe nikoli termodynamicky, ale z hlediska statistiky a pravděpodobnosti. Přítomnost těles mění rozložení entropie a vzniká entropická síla, kterou ztotožňuje s gravitačním působením. Plošné zdroje entropie opět vedou na správný gravitační zákon. V roce 2016 přidává Erik Verlinde i objemový zdroj entropie související s fluktuacemi vakua, které jsou při kvantových procesech nevyhnutelné [3]. Tím poprvé dostává teorii, která v některých případech dává jiné výsledky než obecná relativita, což je experimentálně ověřitelné.

Šestice toeretiků, která nejvíce přispěla k pochopení vztahu mezi
termodynamikou, statistikou, teorií informace a gravitací.

Entropie a tři Verlindovy principy

Entropie byla původně definována v termodynamice jako poměr tepla dodaného do systému a absolutní teploty (dS = dQ/T). Takto upravené teplo má vlastnosti úplného diferenciálu, což vede na příjemnou vlastnost: entropie mezi dvěma stavy systému nezávisí na způsobu, jak se systém z jednoho stavu do druhého dostal (o teplu totéž říci nelze). Ve statistice má entropie význam logaritmické míry pravděpodobnosti realizace stavu a v kvantové teorii je logaritmickou mírou počtu kvantových stavů, kterými lze daný makroskopický stav realizovat. Entropie tak souvisí s „množstvím chaosu“ v systému. V informatice entropie popisuje množství informací. V uzavřeném systému může entropie jen růst, tomuto tvrzení říkáme druhá věta termodynamická. V termodynamické rovnováze dosáhne entropie svého maxima. Gradient (spád entropie) vede na vznik makroskopických sil. Typickým příkladem je „síla“ nutící vůni z rozbité lahvičky voňavky zaplnit celou místnost, v tomto případě hovoříme o difúzi. Obdobnou entropickou silou je osmóza (prosakování rozpouštědla skrz membránu) vedoucí na vznik osmotického tlaku. Ve změnách entropie má původ i obyčejná elasticita gumičky. Koneckonců i tlak plynu na stěnu má původ v chování velkého souboru systémů navenek. Jedna částice tlak nikdy nevytvoří, velký soubor částic ano. Verlinde věří, že i gravitaci lze chápat jako entropickou sílu, tedy důsledek statistického působení mnoha mikroskopických kvantových systémů. Entropická síla způsobuje pohyb těles, s nímž souvisí mechanická práce Fdx. Ta by měla být rovna teplu odpovídajícímu změně entropie, tedy TdS = Fdx. Pro znalce diferenciálního počtu lze tuto jednoduchou rovnici přepsat jako F = T grad S.

Verlinde postavil svou teorii na třech principech. První už jsme zmínili. Gravitace je entropickou silou. Další dva principy řeší, kde jsou zdroje entropie. Ty by měly být dvojí: jednak plošné (druhý princip, 2010) a jednak objemové (třetí princip, 2016). Plošné zdroje souvisí s holografickým principem. V okolí mikroskopického objektu by měla existovat jakási projekční plocha, na níž je veškerá informace o objektu. A na této ploše je lokalizován jeden ze dvou zdrojů entropie. Druhý zdroj entropie respektuje Heisenbergovy relace neurčitosti. U mikroskopického objektu nelze nikdy současně změřit polohu a hybnost. Obdobné relace platí i pro všechna pole. Ve vakuu nemůže být současně nulová hodnota pole a nulová hybnost pole. To vede k nenulovým fluktuacím všech polí, které jsou zdrojem objemové složky entropie.

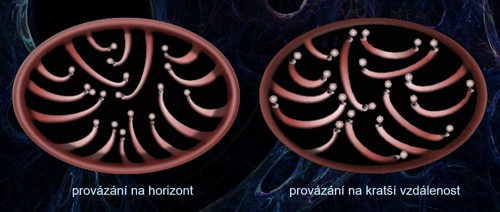
Vakuové fluktuace polí jsou obecně považovány za zdroj zrychlené expanze vesmíru, tedy za původce temné energie. Ve Verlindově teorii záleží na tom, jak jsou vlnové funkce těchto fluktuací vzájemně provázány. Buď je to na vzdálenosti kratší než k horizontu viditelného vesmíru, nebo až na horizont. Každá varianta přispívá k objemové složce entropie jinak, což by mohlo být rozpoznatelné na skutečném průběhu zrychlené expanze vesmíru. Zdroj: [3].

Možnosti ověření

Podle Verlindových analýz je plošná entropie (S_A) zdrojem běžné gravitační síly, tedy ubývající s druhou mocninou vzdálenosti od objektu. Objemová složka entropie (S_V) ale přináší jinou závislost připomínající poněkud snahy zastánců modifikovaní gravitace (MONDMOND – Modified Newtonian Dynamics, úpravy Newtonových zákonů, které měly za cíl vysvětlit rozdělení rychlostí hvězd v galaxiích jinak než za pomoci temné hmoty. ). V každém případě vede objemová složka na zrychlenou expanzi s nenulovou kosmologickou konstantouKosmologická konstanta – člen v Einsteinových rovnicích obecné relativity, který je úměrný metrickému tenzoru (Λg_μν). Albert Einstein ho zavedl v roce 1917. Jeho účelem bylo, aby rovnice poskytovaly stacionární řešení. Po objevu expanze vesmíru v roce 1929 se tento člen jevil jako zbytečný. Moderní kosmologie o něm opět uvažuje v souvislosti s popisem zrychlené expanze vesmíru. Hodnota Λ odhaduje na Λ ~ 2×10⁻⁵² m⁻². v Einsteinových rovnicích obecné relativity. Velmi důležitý je fakt, že samotná přítomnost látky snižuje objemovou složku entropie a navíc vede k jejímu přerozdělení. Poměr S_V/S_A tedy závisí na průměrné hustotě okolního prostředí. V hustých oblastech, například ve Sluneční soustavě, je tento poměr velmi malý a vede na předpovědi ve shodě s obecnou relativitou. V limitě S_V/S_A › 0 dává Verlindova teorie přesně obecnou relativitu. V oblastech s nízkou hustotou energie, například pro galaxii jako celek, už je ale objemovou složku entropie třeba započíst, což vede na ploché rotační křivky, podobné těm, které se měří v periferních oblastech spirálních galaxií a které jsou chápány jako důsledek existence galaktického haló z temné hmoty. Verlindovo pojetí tak považuje temnou energiiTemná energie – entita zodpovědná za zrychlenou expanzi vesmíru, která byla objevena na konci roku 1998 (Saul Perlmutter, Adam Riess). Temná energie tvoří 68 % hmoty a energie ve vesmíru. Hustota temné energie je velmi málo proměnná v čase i v prostoru, pokud vůbec. Nejnadějnějším kandidátem na temnou energii je energie vakuových fluktuací. a temnou hmotuTemná hmota – hmota ve vesmíru nebaryonové povahy, která není složena z kvarků. Temná hmota udržuje pohromadě svítící objekty velkých rozměrů, které díky ní v periferních oblastech obíhají rychleji, než odpovídá gravitačnímu zákonu aplikovanému na viditelnou hmotu. Podle posledních odhadů na základě pozorování existuje ve vesmíru 5 % baryonové hmoty, 27 % temné hmoty a 68 % temné energie. Existuje několik hypotetických částic, které jsou vhodnými kandidáty na částice temné hmoty, dosud však nebyly objeveny. Termín „temná hmota“ zavedl v roce 1933 Fritz Zwicky, když zjistil, že se členové Kupy galaxií ve Vlasech Bereniky pohybují v průměru rychleji, než by odpovídalo gravitačním účinkům viditelné látky. Existují také teorie, které se pokoušejí vysvětlit rotační křivky galaxií a pohyby galaxií v kupách jiným způsobem než temnou hmotou. za pouhý rub a líc jediné mince – za projevy objemové složky entropieEntropie – v termodynamice je definována vztahem dS = dQ/T, kde dQ je diferenciál tepla a T je absolutní teplota (1/T je integrační faktor). Takto zavedená entropie je na rozdíl od tepla úplným diferenciálem, její integrál nezávisí na cestě ve stavovém prostoru. Ve statistice má entropie význam logaritmické míry pravděpodobnosti realizace stavu, v kvantové teorii je logaritmickou mírou počtu kvantových stavů, kterými lze daný makroskopický stav realizovat. Entropie tak souvisí s „množstvím chaosu“ v systému. V informatice entropie popisuje množství informací. V uzavřeném systému může entropie jen růst. V termodynamické rovnováze dosáhne svého maxima.. Veškeré výpočty jsou bohužel zatím prováděny jen pro sféricky symetrické rozložení hmoty, a tak má tato nezvyklá hypotéza ještě vůči svým předchůdcům co dohánět. Sympatické je, že se v posledních dvou letech objevila řada měření, viz například [4–8], jejichž autoři se snaží předpovídané odchylky od obecné relativity ověřit experimentálně. Sady dat jsou ale zatím malé, a proto autoři studií nedocházejí k jednoznačným závěrům – zkrátka jedni Verlindovu hypotézu potvrzují a druzí vyvracejí. Na osud gravitace, která se vynoří v makrosvětě jako posel z mikrosvěta (anglicky Emergent Gravity, česky vynořivší se gravitace), si tedy budeme muset nějakou dobu ještě počkat. Jen budoucnost ukáže, zda je gravitace skutečnou silou, nebo pouhou iluzí.

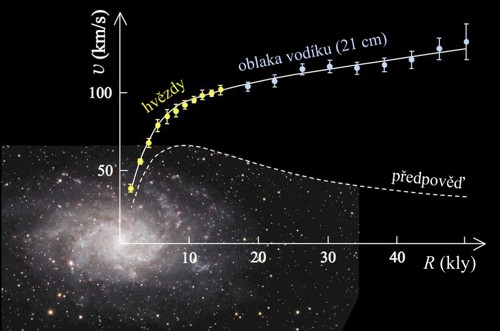
Jsou ploché rotační křivky na periferii spirálních galaxií důsledkem existence
temné hmoty, nebo projevem objemové složky entropie? Zdroj: [3].

Odkazy