|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Mohou stroje nabýt vědomí?
David Zoul
Spintronika a kvantové počítače
V klasické teorii informace je počet možných stavů elementů informace reprezentován body v 2n-dimenzionálním vektorovém prostoru (stavové prostory se kombinují jako kartézský součin). V kvantové teorii informace je systém složený z n qubitů reprezentován body v 2n-dimenzionálním komplexním Hilbertově prostoruHilbertův prostor – úplný lineární vektorový prostor se skalárním součinem. V kvantové teorii odpovídá každý kvantový stav paprsku v Hilbertově prostoru (všem nenulovým násobkům nějakého prvku). Lineární kombinace prvků odpovídají superpozici stavů. Vlastnosti Hilbertova prostoru umožňují hovořit o změnách stavu systému v geometrických pojmech, jako jsou projekce, rotace, zrcadlení apod. (stavové prostory se kombinují jako tenzorový součin). Tato skutečnost umožňuje exponenciální urychlení výpočtů na kvantových počítačích ve srovnání s klasickými. Na rozdíl od běžného procesoru, ve kterém každý tranzistor může nabývat hodnoty buď 0, nebo 1, kvantový tranzistor může nabývat obou těchto hodnot v jednom okamžiku. 16-bitový procesor může v jednom okamžiku počítat jen s jednou z 65 tisíc hodnot, ale 16-qubitový procesor může počítat s 65 tisíci hodnotami naráz díky kvantové superpozici.

Komerčně prodávaný kvantový počítač společnosti IBM. Tento kus byl instalován
v německém sídle IBM v Ehningenu u Stuttgartu v roce 2021. Zdroj: IBM.
|
Kvantová tečka – quantum dot, ohraničená oblast polovodiče o průměru jednotek až desítek nanometrů a výšce do deseti nanometrů, která je schopná vázat elektrony v důsledku nižší energie vodivostního pásu ve srovnání s okolním polovodičem. Tyto elektrony mohou nabývat pouze diskrétních hodnot energie. Jde vlastně o uměle vytvořenou kvantovou potenciálovou jámu modifikovatelné hloubky. Například v GaAs se dno vodivostního pásu nachází na nižší energetické hladině než dno vodivostního pásu AlGaAs. Obklopíme-li mikroskopický kousek GaAs (o velikosti několika nm) materiálem AlGaAs, vodivostní elektron uvnitř GaAs bude uvězněn v trojrozměrné potenciálové jámě, jejíž parametry se dají přesně nastavit při výrobním procesu. Kvantové tečky se využívají ve speciálních součástkách, které jsou schopny pracovat s jednotlivými elektrony či fotony. Spintronika – spinová elektronika neboli magnetoelektronika. Jde o technologii využívající kvantové vlastnosti spinu elektronu, případně celého atomu. Zatímco klasická elektronika využívá ve všech technologiích pouze náboj elektronu, ve spintronice se kromě náboje elektronu využívá i orientace jeho spinu. První spintronické logické obvody byly zkonstruovány v roce 1997. Kleinův paradox – fyzikální jev, který v roce 1929 předpověděl švédský fyzik Oskar Klein. Jeho teorie popisuje chování rychle se pohybujících elektronů v kvantové jámě. Elektron je z pohledu klasické fyziky například uvězněn uvnitř kvantové tečky. Z pohledu fyziky kvantové sice může „protunelovat“ ven, avšak čím vyšší a silnější bariéru použijeme, tím menší je pravděpodobnost takového procesu. Klein vyslovil teorii, že pokud by rychlost elektronu byla dostatečně vysoká, ani libovolně silná bariéra elektronu v úniku nezabrání. Soudilo se, že tyto podmínky jsou možné jen například v blízkosti černých děr. Avšak s objevem grafenu je poměrně reálné, že tento jev bude pro kvazičástice ověřen za vynaložení mnohem menší energie, a to již v poměrně blízké budoucnosti. Optická pinzeta – laserové zařízení pro manipulaci s průsvitnými mikroskopickými objekty. Fokusovaný laserový paprsek vytváří optickou past, ve které lze objekt držet jako v pinzetě. Posunováním paprsku se přemísťuje i vybraný objekt. Laserový paprsek vytváří malou sílu (obvykle v řádu piconewtonů), v závislosti na relativním indexu lomu mezi částicemi a okolním médiem. K optické levitaci dochází tehdy, pokud síla světla překoná gravitační sílu. Zachycené částice mají obvykle velikost mikronů nebo menší. Fermiho moře – uskupení fermionů, které vyplňují kvantové stavy s nejnižší energií, které daný kvantový systém umožňuje. Fermiony s nejvyšší energií tvoří energetickou hladinu nazývanou Fermiho hladina, a slovem moře vyjadřujeme podobnost s vodním útvarem, který vyplňuje prostor s nejnižší gravitační potenciální energií a tvoří povrch v určité výšce. Při teplotě 0 K jsou všechny elektrony ve Fermiho moři a Fermiho hladina je maximální energií kteréhokoli z nich. Malé množství energie (například teplo, které nepatrně zvedne teplotu) ovlivňuje pouze elektrony na povrchu Fermiho moře nebo v jeho blízkosti. Elektrony pod povrchem Fermiho hladiny jsou chráněny: takové elektrony obecně potřebují dostatek dodatečné energie, aby se dostaly na energetické hladiny vyšší, než je Fermiho hladina. Elektrony na nebo nad Fermiho hladinou mají mnohem větší pravděpodobnost, že změní polohu, například v reakci na elektrické pole, čímž vytvoří vodivostní proud. Mřížková konstanta – parametr mřížky, označuje rozměr základních buněk v krystalové mřížce. Třírozměrní mřížky mají obecně tři mřížkové konstanty, označované jako a, b a c. Ve zvláštním případě kubických krystalových struktur jsou však všechny konstanty stejné a jsou označovány jako a. |
Kvantové teleportační obvody
Kvantová teleportace umožňuje přenos informace o kvantovém stavu mikroobjektu, a tím v podstatě dovoluje manipulaci se stavy jednotlivých mikročástic. Kvantové počítače zpracovávající informace uložené v qubitechQubit – kvantová verze bitu neboli kvantový bit, základní jednotka informace podléhající kvantové logice. Klasický bit je buď ve stavu |0⟩, nebo |1⟩. Qubit zahrnuje navíc všechny superpozice α|0⟩+β|1⟩. Konkrétní hodnotu |0⟩, nebo |1⟩ nabude teprve v okamžiku měření. Element kvantové informace zavedl Benjamin Schumacher roku 1995. Na qubit lze také pohlížet jako na virtuální částici a v analogii k antičásticím lze zavést rovněž antiqubit nesoucí zápornou informaci. a ebitechEbit – entanglovaný neboli provázaný bit. Provázané qubity jsou základem kvantového počítače., slibují s použitím neklasických algoritmů efektivně řešit úlohy, které svojí náročností stojí daleko za hranicí jakéhokoli myslitelného počítače založeného na klasické von Neumannově platformě. Kvantové zpracování informace se opírá o určité elementární operace, analogické k působení hradla v polem řízeném tranzistoru (FETFET – Field-Effect Transistor, tranzistor řízený elektrickým polem. Tvar a vodivost kanálu mohou být ovlivněny napětím přiloženým k řídící elektrodě. Součástku patentoval v roce 1930 Julius Edgar Lilienfeld, americký inženýr rakousko-uherského původu.). Proto se těmto operacím říká kvantové hradlo (quantum gate). Může to být například elektrické či magnetické pole přiložené k jednomu či dvěma qubitům tak, že řízeným způsobem mění jejich kvantový stavKvantový stav – soubor pozorovatelných parametrů kvantového systému, kterými je systém plně charakterizován. Popis stavu musí respektovat omezení kvantové mechaniky na současnou měřitelnost či neměřitelnost veličin. Například základní energetický stav atomu značíme symbolem |S>, vakuový stav symbolem |0>, živou kočku označíme |Ž>, mrtvou kočku |M> a podobně. Kvantový stav je zpravidla charakterizován sadou kvantových čísel a je matematicky vyjádřen tzv. vlnovou funkcí (prvkem Hilbertova prostoru stavů).. Úlohu qubitu může hrát například spinSpin – vlastní (vnitřní) rotační moment částice souvisící s Lorentzovou symetrií. Pro částici v centrálním poli se přirozeným způsobem skládá s momentem hybnosti. Částice s nenulovým spinem se mohou chovat jako elementární magnetické dipóly μ, aniž by měly elektrický náboj. Takové částice reagují na vnější magnetická pole., Josephsonův přechodJosephsonův jev – jev, při kterém dva supravodiče oddělíme tenkou vrstvou izolantu tak, aby Cooperovy páry mohly tunelovat izolantem. Rozhraním poteče elektrický proud, jehož velikost závisí na vnějším magnetickém poli a teplotě. Využívá jej například senzor magnetického pole SQUID (Superconducting Quantum Interference Device). Součástka založená na Josephsonově jevu se nazývá Josephsonův spoj., nebo elektron v polovodičové kvantové tečceKvantová tečka – quantum dot, ohraničená oblast polovodiče o průměru jednotek až desítek nanometrů a výšce do deseti nanometrů, která je schopná vázat elektrony v důsledku nižší energie vodivostního pásu ve srovnání s okolním polovodičem. Tyto elektrony mohou nabývat pouze diskrétních hodnot energie. Jde vlastně o uměle vytvořenou kvantovou potenciálovou jámu modifikovatelné hloubky. Například v GaAs se dno vodivostního pásu nachází na nižší energetické hladině než dno vodivostního pásu AlGaAs. Obklopíme-li mikroskopický kousek GaAs (o velikosti několika nm) materiálem AlGaAs, vodivostní elektron uvnitř GaAs bude uvězněn v trojrozměrné potenciálové jámě, jejíž parametry se dají přesně nastavit při výrobním procesu. Kvantové tečky se využívají ve speciálních součástkách, které jsou schopny pracovat s jednotlivými elektrony či fotony.. Z formálního hlediska se kvantovým hradlem rozumí kvantová analogie logických hradel používaných v reverzibilním (vratném) počítání (myslí se tím vratnost termodynamická). Možnost vratného počítání objevil již Charales. H. Bennett v roce 1973, jeho využití v kvantovém počítání však bylo umožněno až po objevu základního faktu, že časová evoluce izolovaného kvantového systému, popsaná příslušným hamilotoniánem, je vratnou dynamikou, která odráží kroky vratného booleovského počítání (R. Feynman, P. A. Benioff, 1982). Tím se kruh uzavřel a stačilo jen přepsat základní konstrukce hradel používaných pro vratné počítání, do jejich kvantových analogů.

Paul A. Benioff (*1947), Chris P. Williams (*1976)
Stejně jako u kvantové teleportace, také v případě kvantového počítání hrají důležitou roli entanglované páry částic. Kvantová teleportace by se tak mohla významně uplatnit při přenosu informací v kvantových počítačích. První představy o teleportačních obvodech pro kvantový počítač byly popsány již v práci C. P. Williamse a S. H. Clearwatera s názvem Explorations in Quantum Computing z roku 1998.
Dekoherence
Vlnová funkce při kontaktu s vnějším světem zkolabuje. Kvantový počítač je tedy jakousi černou skřínkou, v níž výpočetní proces probíhá zcela izolovaně od okolí. Extrémní závislost kvantových počítačů na vnějších vlivech je jednak problémem při jejich konstrukci, jednak působí problémy při zápisu dat a jejich čtení – vstup i výstup dat jsou destruktivními interakcemi. Proces výpočtu je tedy třeba nechat proběhnout celý najednou a až pak odečíst výsledek – přičemž nutně způsobíme kolaps procesu. Poté kvantový výpočet opět restartuje. Protože v kvantovém počítači dříve či později dojde k destruktivní interakci s okolím, musí příslušný výpočet proběhnout dostatečně rychle. Frekvence kvantového počítače, potřebná k tomu, aby ještě před kolapsem vlnové funkce stihl dokončit nějaký prakticky použitelný výpočet, musí být proto velmi vysoká – mnohem vyšší než u konvenčních počítačů.
Josephsonův přechod (1962) a kvantový tranzistor
Nosiči náboje v supravodiči jsou tzv. dielektrony, čili
Cooperovy páry. Jedná se o bosonyBosony – částice, které mají celočíselný spin, symetrickou vlnovou funkci, nesplňují Pauliho vylučovací princip a podléhají Boseho-Einsteinově statistickému rozdělení. Například jsou to všechny skalární i vektorové mezony, fotony a gluony. Při nízkých teplotách se bosony mohou hromadit v základním stavu.
tvořené tzv. kvantovým kondenzátem dvojice elektronů s navzájem opačně
orientovanými spiny, plovoucími volně ve Fermiho mořiFermiho moře – uskupení fermionů, které vyplňují kvantové stavy s nejnižší energií, které daný kvantový systém umožňuje. Fermiony s nejvyšší energií tvoří energetickou hladinu nazývanou Fermiho hladina, a slovem moře vyjadřujeme podobnost s vodním útvarem, který vyplňuje prostor s nejnižší gravitační potenciální energií a tvoří povrch v určité výšce. Při teplotě 0 K jsou všechny elektrony ve Fermiho moři a Fermiho hladina je maximální energií kteréhokoli z nich. Malé množství energie (například teplo, které nepatrně zvedne teplotu) ovlivňuje pouze elektrony na povrchu Fermiho moře nebo v jeho blízkosti. Elektrony pod povrchem Fermiho hladiny jsou chráněny: takové elektrony obecně potřebují dostatek dodatečné energie, aby se dostaly na energetické hladiny vyšší, než je Fermiho hladina. Elektrony na nebo nad Fermiho hladinou mají mnohem větší pravděpodobnost, že změní polohu, například v reakci na elektrické pole, čímž vytvoří vodivostní proud., a držícími pohromadě díky fononůmFonon – kvazičástice vibrací krystalové mříže, vibrační kvantum šířící se krystalovou mříží. Pomocí fononů lze popisovat šíření zvukových vln v pevných látkách. Samotný název fonon vznikl jako analogie k fotonu. Foton je částicí elektromagnetického pole, fonon je kvazičásticí netlumeného zvukového pole v pevné látce..
Enrico Fermi (1901–1954)
Podstatou Cooperova jevu je nestabilita Fermiho moře vzhledem k tvorbě Cooperových párů. Z kvantové mechaniky víme, že každou interakci si lze znázornit jako výměnu virtuálních bosonů existujících po dobu Δt, která je slučitelná s principem neurčitosti. V případě Cooperova párování jsou oněmi bosony kvazičástice zvané fononyFonon – kvazičástice vibrací krystalové mříže, vibrační kvantum šířící se krystalovou mříží. Pomocí fononů lze popisovat šíření zvukových vln v pevných látkách. Samotný název fonon vznikl jako analogie k fotonu. Foton je částicí elektromagnetického pole, fonon je kvazičásticí netlumeného zvukového pole v pevné látce.. Fonony se pohybují rychlostí zvuku v daném prostředí, s energií h? a hybností hk. Podstatným rysem každého energetického kvanta je jeho úměrnost frekvenci. Vysokofrekvenční fonony mohou zvyšovat svoji frekvenci jen po relativně velkých skocích. Pravděpodobnost, že mód s frekvencí ω bude vůbec vybuzen je dána Planckovým faktorem
| \[w = \exp \left( { - \frac{{\hbar \omega }}{{{k_{\rm{B}}}T}}} \right)\,,\] | (1) |
a proto módy s \(\hbar \omega \le {k_{\rm{B}}}T\) budou již zanedbatelně přispívat k celkové energii. Jak teplota stoupne nad absolutní nulu, bude se zvětšovat počet užitečných módů (těch s \(\hbar \omega \le {k_{\rm{B}}}T\)). Počet přispívajících módů pak bude (kmitočet \(f = \omega /2\pi \))
| \[n\left( T \right) \approx \frac{V}{{6{\pi ^2}{f^3}}}{\left( {\frac{{{k_{\rm{B}}}T}}{\hbar }} \right)^3},\] | (2) |
odkud obdržíme tzv. Debyeovu teplotu
| \[{\theta _{\rm{D}}} = \frac{{hf}}{{{k_{\rm{B}}}}} = {\left( {\frac{{6{\pi ^2}n}}{V}} \right)^{{\textstyle{1 \over 3}}}}\frac{\hbar }{{{k_{\rm{B}}}}}f = {\left( {\frac{{6{\pi ^2}}}{{{a^3}}}} \right)^{{\textstyle{1 \over 3}}}}\frac{\hbar }{{{k_{\rm{B}}}}}f,\] | (3) |
kde a je mřížková konstanta. U fononů se tedy jedná o kolektivní excitace krystalové mříže, jež mají v mřížce jisté spektrální rozdělení a svůj maximální kmitočet daný vztahem
| \[{f_{\max }} = \frac{{{k_{\rm{B}}}{\theta _{\rm{D}}}}}{h}\] | (4) |
Vyšší frekvence již nemají smysl, neboť by jejich vlnová délka byla menší než vzdálenost mezi atomy. Elektrony si tedy mohou vyměňovat s mřížkou fonony o kmitočtu 0 až fmax. Na obrázku 1 je znázorněn Feynmanův diagram tohoto procesu. Elektron s vlnovým vektorem k vyzáří během své dráhy fonon s vlnovým vektorem q a změní svůj vektor na k − q. Při tomto procesu musí platit zákon zachování hybnosti a energie. Vyzářený fonon bude poté absorbován dalším elektronem s vlnovým vektorem –k.
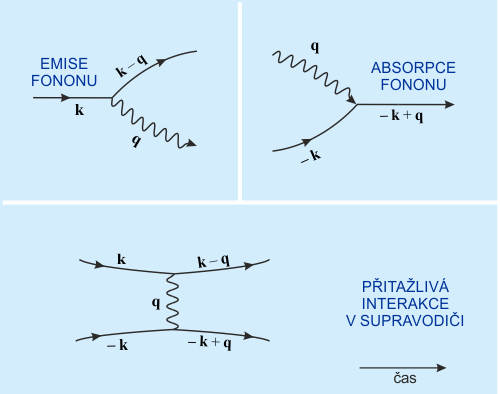
Obr. 1: Feynmanovy diagramy pro emisi, absorpci a výměnu fononu q mezi dvěma elektrony s vlnovými vektory (k, −k). Převládne-li tato přitažlivá interakce nad coulombovskou odpudivou interakcí v kovové mřížce, vznikne supravodivý stav.
Zatímco ve vakuu, kde žádné fonony nejsou, se elektrony pouze elektrostaticky odpuzují, v krystalové mřížce kovu se mohou i přitahovat. Je to podobná přitažlivá síla, která působí mezi loďkami na rozvlněné hladině. Když se k sobě přiblíží, vznikne mezi loďkami „stín“, který omezuje šíření vln kratších vlnových délek, protože ty nedokážou obě lodi tak dobře „obcházet“. V konečném důsledku je mezi loděmi hustota vln nižší a energie okolních vln stlačuje obě lodi k sobě. Staré námořnické příručky dokonce obsahovaly zákaz vplouvání více lodí do přístavu za rozbouřeného počasí současně. Přitažlivá síla by totiž mohla vzrůst při přiblížení lodí natolik, že by se navzájem roztříštily.
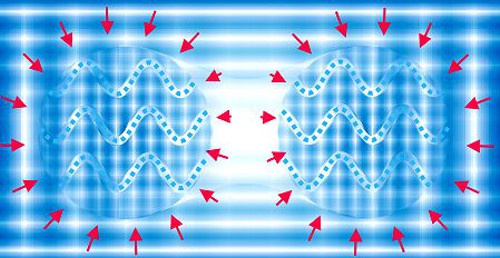
Obr. 2: Schematické vyjádření Cooperova párování
Náboj supravodivých nosičů (dielektronů) je q = 2e a jejich hmotnost m = 2me. Vlnové funkce kondenzátů ve dvou supravodičích umístěných těsně u sebe a oddělených velmi tenkou nevodivou bariérou (tzv. Josephsonův přechodJosephsonův jev – jev, při kterém dva supravodiče oddělíme tenkou vrstvou izolantu tak, aby Cooperovy páry mohly tunelovat izolantem. Rozhraním poteče elektrický proud, jehož velikost závisí na vnějším magnetickém poli a teplotě. Využívá jej například senzor magnetického pole SQUID (Superconducting Quantum Interference Device). Součástka založená na Josephsonově jevu se nazývá Josephsonův spoj.), nejsou navzájem nezávislé. Supravodiče jsou spolu slabě vázané a vlnové funkce jsou koherentní, čili udržují si stálý fázový rozdíl. Tento rozdíl určuje, jakým směrem a v jakém počtu budou Cooperovy páry přes bariéru tunelovat. Fázový rozdíl je určen teplotou supravodičů a indukcí vnějšího magnetického pole.

Petrus Josephus Wilhelmus Debye (1884–1966), Brian David Josephson (*1940),
Leon Neil Cooper (*1930)
Pro funkci Josephsonova přechodu je důležitá správná tloušťka izolační vrstvy. Musí být menší než tzv. koherenční délka, která je u kovů řádově stovky až tisíce nanometrů, jinak se Cooperovy páry rozpadají. Nesmí ale být příliš tenká, jinak je Josephsonův jev velmi slabý. V praxi se používá jako supravodič například niob pokrytý vrstvou oxidu hlinitého, jejíž tloušťka je s koherenční délkou srovnatelná, tedy několik desetin mikrometru.
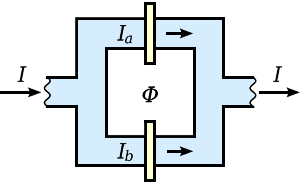
Obr. 3: Smyčka ze dvou Josephsonových přechodů. Zdroj: Wikimedia Commons.
Procesory založené na kvantovém annealingu
Jedná se o procesory schopné provádět optimalizaci spočívající v hledání maxim a minim ve stavovém prostoru, což v celé řadě aplikací vede k vyřešení složitých problémů. Annealing (česky ochlazování) zde znamená, že když algoritmus uvízne v lokálním minimu/maximu, pokračují kvantové pokusy o nalezení dalších extrémů, dokud není dosaženo globálního extrému.
První experimentální 5-qubitový kvantový procesor pracující na tomto principu představila firma IBM roku 2000. První komerčně vyráběný 128-qubitový kvantový procesor Rainier byl uveden na trh v roce 2011 společností D-WAVE. Byl vyroben ze supravodivého niobu chlazeného kapalným heliem. Běžel na frekvenci 100 GHz. Obsahoval 16 jader, z nichž každé bylo tvořeno 1 500 supravodivých Josephsonových smyček v roli kvantových tranzistorů, pracujících s kvanty magnetického toku – fluxony – v roli qubitů. Následně proběhl úspěšný vývoj cenově mnohem výhodnějšího kvantového procesoru na bázi supravodivého křemíku.

Obr. 4: Procesor pracující na principu kvantového annealingu.
Zdroj: D-Wave systems.

Obr. 5: První komerčně vyráběný
optimalizér pracující na principu
kvantového annealingu. Zdroj: D-Wave systems.

Obr. 6: V roce 2013 uvedla společnost D-Wave na trh druhou řadu kvantových optimalizérů (D-Wave two), vybavených již 512-qubitovým procesorem. Cena se pohybovala okolo 15 miliónů dolarů.. Zdroj: D-Wave systems.
Počítače založené na kvantovém provázání
První kvantové procesory byly použitelné víceméně jednoúčelově pro řešení komplikovaných matematických problémů, na které konvenční počítače nestačí, jako je například faktorizace, diskrétní optimalizace či dešifrování. Roku 2017 představila firma IBM první kvantový počítač založený na provázání kvantových stavůProvázaný stav – entanglement, kvantově korelovaný stav systému dvou a více částic, v němž nemá smysl mluvit o stavech jednotlivých složek. Například z provázaného stavu dvojice fotonů nelze vyjádřit stavy jednotlivých fotonů. Značíme |AB>+|XY>, což znamená, že najdeme-li první částici ve stavu A, je druhá ve stavu B. Je-li první ve stavu X, pak druhá je ve stavu Y. Měřením provedeným na jedné částici se dozvíme určitou informaci o částici druhé. Je to způsobeno tím, že mají společnou minulost. Někdy se také hovoří o propletených stavech. (entanglementu), disponující 50 qubity. Společnosti IBM se podařilo udržet qubity v koherentním stavu po dobu 90 mikrosekund. Jednalo se o první zařízení tohoto typu, které se přiblížilo k takzvané quantum supremacy, neboli kvantové nadvládě. Stavu, kdy kvantový počítač dokáže provádět úkony nad možnostmi konvenčních superpočítačů.

Obr. 7: Kvantový počítač s 50 provázanými qubity společnosti IBM. Zdroj: IBM.
Kvantová nadvláda
Roku 2019 se vědcům z Googlu a NASA podařilo vytvořit 53 qubitový kvantový počítač Sycamore, který poprvé dosáhl kvantové nadvlády. To představuje situaci, kdy kvantový počítač vyřeší úlohu, která by nejvýkonnějšímu konvenčnímu superpočítači současnosti trvala výrazně delší dobu. Konkrétně 3 minuty a 20 sekund zabralo počítači Sycamore vyřešit speciální úlohu, kterou by tehdy nejvýkonnější superpočítač planety – americký SUMMIT – řešil 2,5 dne.

Obr. 8: Celkový pohled na kvantový počítač Sycamore. Zdroj: Google.

Obr. 9: Vlevo kvantový procesor firmy GOOGLE, vpravo pohled do útrob kvantového počítače Sycamore který jako první prolomil hranici quantum supermacy. Zdroj: Google.

Obr. 10: Americký konvenční (nekvantový) superpočítač Summit dosáhl roku 2018 výkonu 200 petaflopsFlops – zkratka pro počet operací v pohyblivé řádové čárce za sekundu (FLoating-point Operations Per Second), což je obvyklé měřítko výpočetní výkonnosti počítačů.. Používá systém IBM AC922, který tvoří celkem 4 608 serverů. Každý z těchto serverů přitom obsahuje dva 22-jádrové procesory IBM Power 9, plus šest grafických jednotek NVIDIA Tesla V100. Tuto architekturu superpočítače podporuje paměť o velikosti přes 10 PB a vysokorychlostní propojení.. Zdroj: IBM.
Kvantové výpočetní stroje v současnosti dokážou vypočíst například struktury složitých molekul, pomáhají při hledání nových léčiv a dalších velmi specifických úlohách. Zatím se ale nikomu nepodařilo postavit univerzální kvantový počítač. Stavbu jednoho takového letos započala firma IBM v Kanadě. Jeho spuštění je plánováno na rok 2023. Pokud se vše podaří, bude to znamenat technologickou revoluci. Výpočetní výkon poskočí o mnoho řádů, což mj. výrazně posune vývoj mnoha algoritmů pro umělou inteligenci. Jediný takový stroj by nahradil všechny superpočítače světa dohromady a v krátkém čase by například dokázal rozluštit současné bezpečnostní šifry. Již dnes proto vědci vyvíjejí kryptoalgoritmy, které by dokázaly odolat i kvantovým počítačům.
Možné realizace spintronického tranzistoru nad teplotou kapalného helia
Všechny dosud realizované kvantové logické obvody je nutno chladit na teplotu kapalného hélia. Jedním z možných východisek je růst Mn-dopovaného GaAs na atomární úrovni, čímž vznikne feromagnetický a elektricky dopovaný polovodič pracující při teplotě kapalného dusíku.
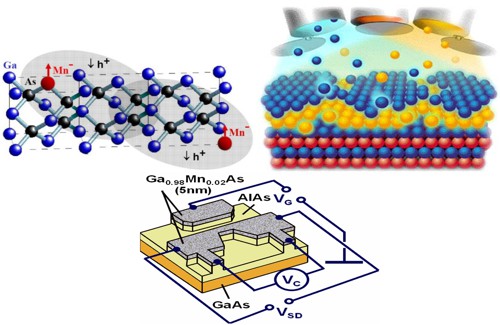
Obr. 11: První úspěšná vysokoteplotní realizace: Spinový Hallův tranzistor.

Edwin Herbert Hall (1855–1938), Tomáš Jungwirth (*1967)
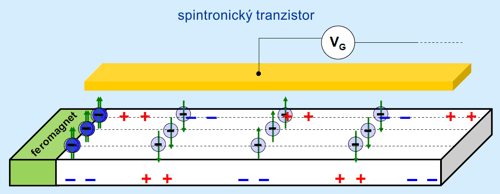
Obr. 12: Injektované spinově polarizované proudy budí příčné elektrické napětí.
Spiny působí na proud a proud zpětnovazebně působí na spiny.
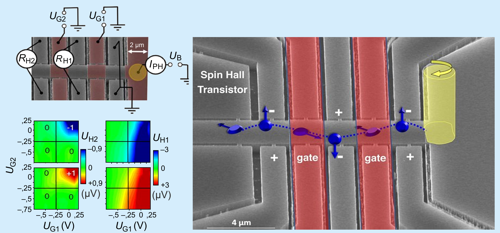
Obr. 13: Tranzistor může pracovat za pokojové teploty, avšak tranzistorový jev je
prozatím příliš slabý z hlediska možnosti využití v mikroprocesoru.
Grafen
GrafenGrafen – jedna z mnoha forem uhlíku. Jde o atomární monovrstvu či dvojvrstvu složenou z pravidelných šestiúhelníků, která má mimořádnou pevnost a vysokou elektrickou i tepelnou vodivost. Má revoluční využití v elektrotechnice a jiných oborech. Grafen poprvé připravili v roce 2004 Andrej Geim a Konstantin Novoselov. Za svůj objev získali Nobelovu cenu za fyziku pro rok 2010. je polovodivá uhlíková nanovrstva objevená roku 2004
Andre Geimem a Konstantinem Novoselovem
(Nobelova cena za fyziku 2010), umožňující pracovat až v terahertzové oblasti,
při téměř nulové efektivní hmotnosti elektronů, které se tak v grafenu pohybují
relativistickými rychlostmi. První grafenové tranzistory s rozměrem 40 nm byly
sestrojeny roku 2011 firmou IBM – běží na frekvenci 155 GHz – viz obr. 14.
Existuje teoretická možnost konstrukce nového typu tranzistoru založeného na
Kleinově paradoxuKleinův paradox – fyzikální jev, který v roce 1929 předpověděl švédský fyzik Oskar Klein. Jeho teorie popisuje chování rychle se pohybujících elektronů v kvantové jámě. Elektron je z pohledu klasické fyziky například uvězněn uvnitř kvantové tečky. Z pohledu fyziky kvantové sice může „protunelovat“ ven, avšak čím vyšší a silnější bariéru použijeme, tím menší je pravděpodobnost takového procesu. Klein vyslovil teorii, že pokud by rychlost elektronu byla dostatečně vysoká, ani libovolně silná bariéra elektronu v úniku nezabrání. Soudilo se, že tyto podmínky jsou možné jen například v blízkosti černých děr. Avšak s objevem grafenu je poměrně reálné, že tento jev bude pro kvazičástice ověřen za vynaložení mnohem menší energie, a to již v poměrně blízké budoucnosti., popřípadě BISFET tranzistoru, tvořeného grafenovou
dvojvrstvou umožňující tvorbu kvantových tečekKvantová tečka – quantum dot, ohraničená oblast polovodiče o průměru jednotek až desítek nanometrů a výšce do deseti nanometrů, která je schopná vázat elektrony v důsledku nižší energie vodivostního pásu ve srovnání s okolním polovodičem. Tyto elektrony mohou nabývat pouze diskrétních hodnot energie. Jde vlastně o uměle vytvořenou kvantovou potenciálovou jámu modifikovatelné hloubky. Například v GaAs se dno vodivostního pásu nachází na nižší energetické hladině než dno vodivostního pásu AlGaAs. Obklopíme-li mikroskopický kousek GaAs (o velikosti několika nm) materiálem AlGaAs, vodivostní elektron uvnitř GaAs bude uvězněn v trojrozměrné potenciálové jámě, jejíž parametry se dají přesně nastavit při výrobním procesu. Kvantové tečky se využívají ve speciálních součástkách, které jsou schopny pracovat s jednotlivými elektrony či fotony. a až tisícinásobnou redukci
spotřeby energie – viz obr. 15.

Obr. 14: První grafenové tranzistory s rozměrem 40 nm byly sestrojeny roku 2011
společností IBM – běží na frekvenci 155 GHz. Zdroj: Lei Liao, Nano Letters.
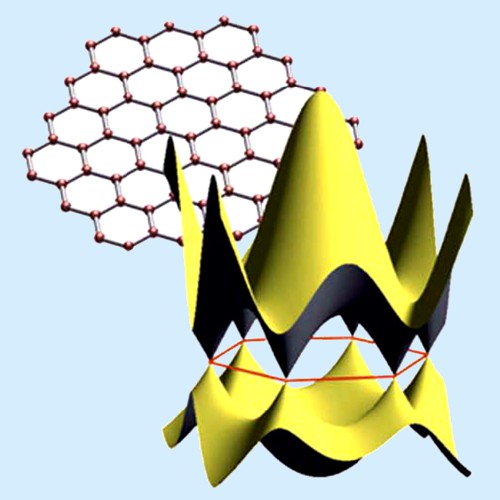
Obr. 15: Teoretická konstrukce kvantové tečky uvnitř grafenové dvojvrstvy.
Zdroj: Condensed Matter.

Andre Geim (*1958), Konstantin Sergejevič Novoselov (*1974)
Diamant
V roce 2012 se podařil významný průlom skupině vědců z Harvardovy univerzity, kteří vytvořili z atomárních nečistot v podobě atomů dusíku kvantové tečky uvnitř krystalicky čistého diamantu. Do těchto kvantových teček se daří opticky umístit kvantové informace a udržet je opticky čitelné po dobu několika sekund i při pokojové teplotě. Objev by mohl v budoucnu vést ke konstrukci optického kvantového procesoru pracujícího za pokojové teploty.
Atomární defekty jsou obecně prostory, kde atomy buď chybí, nebo jsou špatně umístěny ve struktuře materiálu. Tyto defekty mění způsob, jakým se elektrony pohybují v materiálech. V některých materiálech tyto defekty zachycují elektrony, což umožňuje výzkumníkům kontrolu jejich spinů. Na rozdíl od supravodičů se tyto qubity udrží nejen při ultra nízkých teplotách. Mají potenciál mít dlouhou dobu koherence a být vytvářeny ve velkém měřítku.
Zatímco diamanty jsou obvykle ceněny pro jejich dokonalost, jejich vady jsou ve skutečnosti docela užitečné pro qubity. Přidáním atomu dusíku na místo, kde byl v diamantu původně atom uhlíku, se vytvoří vakuová mezera široká dva nanometry. Tato mezera pomáhá prodloužit dobu koherence qubitů a usnadňuje jejich provázání.

Obr. 16: Dusíkové dopanty v diamantu mohou být excitovány zeleným světlem. Diamant, který výzkumníci používají pro své experimenty, obsahuje jen velmi málo defektů dusíku. Na jediném z těchto defektů, takzvaném NV centru, vědci vytvoří kvantový registr, kde demonstrují korekci chyb na kvantovém bitu. Fyzici z univerzity ve Stuttgartu a Institutu Maxe Plancka pro výzkum pevných látek fixují téměř čtvercový diamant o délce čtyř milimetrů a šířce jeden milimetr na zlatý substrát. Adresují elektron jednotlivého dusíkového defektu zeleným laserovým světlem. Dva pásovité řezy ve zlaté fólii vytvářejí úzkou vodivou dráhu, která vede do středu NV. Tato stopa se používá ke generování vysokofrekvenčních pulzů pro manipulaci s jednotlivými jadernými spiny. Zdroj: Gerald Waldherr, Universität Stuttgart.
Nitrid hliníku
Užitečné vady se však neomezují pouze na diamanty. Nitrid hliníku a karbid křemíku jsou levnější, snadněji použitelné a již běžné v každodenní elektronice. Giulia Galli, kvantová chemička a fyzička v Argonnské národní laboratoři a na Chicagské univerzitě spolu se svým týmem našla způsob, jak fyzicky namáhat nitrid hliníku tak, aby se v něm vytvořily elektronové stavy pro qubity. Vzhledem k tomu, že v nitridu hliníku se přirozeně vyskytují izolované atomy dusíku, vědci by měli být schopni řídit spin elektronů v něm, stejně jako v diamantech.

Giulia Galli (*1956). Zdroj: osobní stránka na Chicagské univerzitě.
Hexagonální nitrid bóru
Vědci z Cavendishovy laboratoře na univerzitě v Cambridge ve spolupráci s kolegy z UT Sydney v Austrálii objevili materiál schopný emitovat jednotlivé fotony z atomárních defektů ve své struktuře, a to při pokojové teplotě. Tímto materiálem je hexagonální nitrid boru – levný dvourozměrný materiál, který se pěstuje chemickou depozicí par.
Nedávné výzkumy odhalily přítomnost jednofotonových emisních zdrojů a hustého souboru opticky přístupných spinů. Výzkumníci byli schopni laserem manipulovat se spinem defektů a použít defekty jako úložiště kvantové informace. Světlo emitované z těchto izolovaných defektů nese informaci o spinu, takže tento materiál, pracující i za pokojové teploty, by mohl být užitečný pro kvantové aplikace.
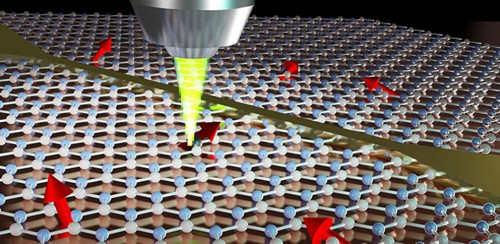
Obr. 17: Zápis kvantových bitů (qubitů) do atomární struktury
hexagonálního nitridu bóru. Zdroj: AI Express.
Jednoatomární kvantové tranzistory
Nově publikované výsledky vědců z Národního institutu standardů a technologií (NISTNIST – National Institute of Standards and Technology, Americký Národní úřad standardů a technologie. Založen byl v roce 1901. Jeho laboratoře se nacházejí v Boulderu (Colorado) a v Gaithersburgu (Maryland).) a Marylandské univerzity ukazují, že se stali teprve druhými na světě, kdo dokázal vytvořit jednoatomový tranzistor a vůbec prvními, kdo vytvořil řadu tranzistorů s jediným elektronem, jejichž geometrie může být manipulována na atomární úrovni.
Vědci byli také schopni získat kontrolu nad fenoménem kvantového tunelování, měnícím rychlost, jakou jednotlivé elektrony cestují fyzickou štěrbinou nebo elektrickou bariérou tranzistoru. Význam tohoto procesu spočívá v tom, že tranzistory se „provážou“ podle zákonů kvantové mechaniky. To může vést k novým způsobům vytváření kvantových bitů (qubitů). Nová metoda představuje klíčové inovace, jako je uzavření atomů fosforu propojenými vrstvami křemíku, které je chrání, a současně posílají elektrony do vložených atomů.
Rydbergovy atomy
Fyzika vysoce excitovaných atomů s velkými rozměry zažívá v posledních letech neuvěřitelný rozmach a objevují se další a další aplikační možnosti. Atomům excitovaným do vysokých energetických stavů říkáme Rydbergovy atomyRydbergův atom – atom excitovaný do vysokého hlavního a vedlejšího kvantového čísla. Rydbergovy atomy jsou velmi citlivé na okolní elektrická a magnetická pole. Elektronová vlnová funkce může být u některých superpozic stavů těchto atomů aproximována klasickým pohybem elektronu po kružnici. Vysoce excitované atomy jsou pojmenovány podle švédského fyzika Johannese Roberta Rydberga (1854–1919).. Mnohdy je lze považovat za makroskopické objekty. Například vodíkový atom excitovaný do stavu s hlavním kvantovým číslem 137 má rozměr jeden mikrometr, což je desettisíckrát větší velikost, než jakou mají běžné atomy. Pokud by se například podařilo excitovat draslík do stavu s hlavním kvantovým číslem 600, měl by atom průměr 0,1 mm, tedy zhruba jako lidský vlas. Nejčastěji se pro přípravu Rydbergových atomů využívá cesium nebo rubidium excitované do stavu s hlavním kvantovým číslem 10 až 50.

Obr. 18: Rydbergův kvantový krystal. Normální atomy (zeleně) jsou uspořádány na optické mřížce. Některé z nich byly laserovým impulzem excitovány do Rydbergova stavu. Jsou znázorněny jako obří fialové koule. Zdroj: Immanuel Bloch.
Vyrobit Rydbergův atom není nic jednoduchého. Atomy musí být drženy v kvantové pasti, ochlazeny na teplotu blízkou absolutní nule (to se zpravidla realizuje technologií laserového ochlazováníLaserové ochlazování – technika využívající k ochlazování atomů laserového světla s vlnovou délkou nepatrně nižší než je charakteristický elektronový přechod v atomu. Toto „podladění“ má za následek, ža atomy absorbují větší množství fotonů, pokud se pohybují směrem ke zdroji, než pokud se pohybují od zdroje. Při interakci s fotonem atom ztrácí odpovídající hybnost ve směru zdroje světla. Při následném vyzáření fotonu sice hybnost opět získá, ale v náhodném směru. Zpravidla se používá šest laserů ve směru a proti směru tří souřadnicových os. Ať se atom vydá kamkoli, vždy proti němu bude svítit laser se správně posunutou frekvencí. Mnohonásobným opakováním lze shluk atomů ochladit na nanokelvinové teploty. V roce 1997 byla za tento objev udělena Stevenovi Chuovi, Claudeovi Cohen-Tannoudjimu a Williamovi Philipsovi Nobelova cena za fyziku.) a excitovány pomocí laserových impulzů do vysokého energetického stavu. Teprve poté je možné je využít k zajímavým experimentům. Jedna z realizací využívá Rydbergovy atomy jako nositele kvantové informace (qubity). Ve stuttgartském 5th Institute of Physics se vědcům podařilo ve skle vytvořit síť mikrokomůrek s atomy, které pak laserem přivedli do Rydbergova stavu. Vzniklé qubity ovládali pomocí laserových impulzů, přivedli je do provázaných stavů a donutili přenášet informaci. Zdá se, že Rydbergovy atomy budou stát u mnoha technologií budoucnosti.
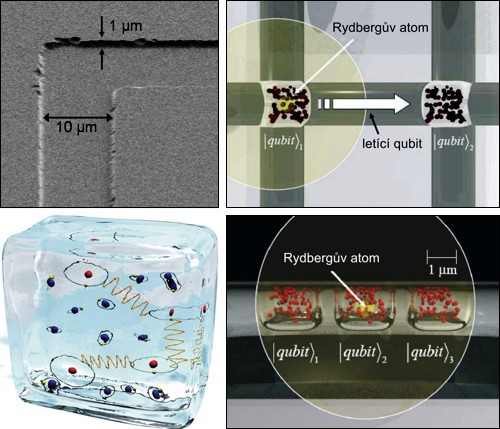
Obr. 19: Základ kvantového počítače budovaného v 5th Institute of Physics ve Stuttgartu. Prostor pro síť qubitů je leptán litograficky do skla. Qubity v mikrokomůrkách ve skle jsou realizovány jako atomy excitované laserem do Rydbergových stavů. Vlevo dole je umělecká představa qubitů „zamrzlých“ ve skle. Zdroj: Stuttgartská univerzita.
SLM qubity
Odborníci z Harvardu pod vedením Sepehra Ebadiho vytvořili prostorový modulátor světla, tzv. SLM (Spatial Light Modulator), který zvládne modulovat vlnovou délku světelných paprsků k tvorbě stovek individuálně zaměřených optických pinzetOptická pinzeta – laserové zařízení pro manipulaci s průsvitnými mikroskopickými objekty. Fokusovaný laserový paprsek vytváří optickou past, ve které lze objekt držet jako v pinzetě. Posunováním paprsku se přemísťuje i vybraný objekt. Laserový paprsek vytváří malou sílu (obvykle v řádu piconewtonů), v závislosti na relativním indexu lomu mezi částicemi a okolním médiem. K optické levitaci dochází tehdy, pokud síla světla překoná gravitační sílu. Zachycené částice mají obvykle velikost mikronů nebo menší. schopných pohybovat jednotlivými atomy. Za tuto techniku byla v roce 2018 udělena Nobelova cenu za fyziku Arthuru Ashkinovi.

Johannes Robert Rydberg (1854–1919), Sepher Ebadi (*1992)
V roce 2017 přišla harvardská skupina s první generací SLM kvantového počítače, kde s pomocí laserových optických pinzet poskládali jednodimenzionální pole vysoce podchlazených rubidiových atomů, které plnili roli 51 qubitů. V dalším kroku rozestavili s pomocí optických pinzet 256 qubitů rovnou do dvoudimenzionálního pole. Výsledkem je něco, co vypadá jako jednoduchý digitální monitor, kde si lze „vyqubitovat“ nějaké obrázky či animace (viz obr 20). Ve skutečnosti je níže uvedená ukázka jen legráckou, dokazující však programovatelnost, tedy schopnost ovlivnit qubity a následně sledovat jejich vzájemné interakce.
Obr. 20: Laser kontrolující pole porovázaných rubidiových atomů a Super Mario, kterého si díky tomu můžete „zapařit“. Fluorescenční zobrazení zviditelňuje qubity v základním stavu. Qubity v Rydbergově stavu jsou umístěny v tmavých bodech mříže. Zdroj: Harvardova univerzita.
Ovlivňování koherenční doby elektromagnetickým polem
Kvantové systémy vydrží ve stavu koherence obvykle jen velice krátce, nanejvýš několik miliontin sekundy. Tým vědců z americké Chicagské univerzity objevil jednoduchý trik, díky němuž mohou kvantové systémy zůstat v operačním stavu, tedy koherentní, tisíckrát déle než doposud – neuvěřitelných 22 milisekund.
David Awschalom a jeho spolupracovníci otestovali svůj objev na pevnolátkových qubitech z karbidu křemíku. Jsou ale přesvědčeni, že by měl fungovat u řady jiných materiálů. Mohl by to být průlom v kvantové komunikaci, počítačových systémech a senzorech. Použití zmíněné úpravy je jednoduché a mělo by odstartovat celé nové směry bádání, které doposud byly kvůli příliš krátkému trvání kvantových stavů prakticky nedostupné.
Jednou z možností kterak zařídit, aby koherence v kvantovém systému vydržela co nejdéle, je důkladná izolace qubitu od všech možných šumů a rušivých jevů v okolí. Další možnost spočívá v použití extrémně čistých materiálů. V obou dvou případech se jedná o velmi náročné a nákladné postupy. Tým z Chicagské Univerzity namísto snahy o eliminaci rušivých šumů z okolí „obrnil“ kvantový systém tak, aby se stal vůči okolnímu rušení netečným.

David D. Awschalom (*1956)
Použili obvyklé elektromagnetické impulzy, kterými se běžně ovládají kvantové systémy, které zkombinovali s kontinuálním střídavým magnetickým polem. Když toto magnetické pole přesně vyladili, přiměli spiny elektronů k rychlé rotaci. Takto uspořádaný systém dokáže téměř úplně eliminovat některé formy rušivých tepelných fluktuací, fyzikálních vibrací a elektromagnetického šumu, které jinak obvykle kvantovou koherenci spolehlivě zničí.
Každý počítač potřebuje způsob, jak číst informace zakódované do jeho bitů. U polovodičových qubitů je typickou metodou čtení adresování qubitů lasery a měření světla vyzařovaného zpět. Tento postup je však náročný, protože vyžaduje velmi účinnou detekci jednotlivých fotonů.
V dalším kroku proto Awshalomův tým použil pečlivě navržené laserové pulzy, kterými dodají nebo nedodají jeden elektron do svého qubitu čímž vytvoří stav buď jedna, nebo nula. Pak je qubit přečten stejným způsobem, tedy laserem. Vyzářené světlo odráží přítomnost či nepřítomnost elektronu, a to s téměř 10 000krát silnějším signálem. Přeměnou křehkého kvantového stavu na stabilní elektronové náboje lze měřit stav mnohem snadněji a získávat mnohem spolehlivější informaci o stavu qubitu. Vyzbrojeni touto metodou se vědci mohli zaměřit na to, aby jejich kvantové stavy trvaly ještě déle.

Obr. 21: Čip použitý v Awshalomově experimentu
je vyroben z levného a běžně
používaného materiálu – karbidu křemíku. Zdroj:
Q-Next.
Vypěstovali vysoce čisté vzorky karbidu křemíku, čímž snížily šum pozadí, který má tendenci zasahovat do fungování qubitů. Poté, aplikací série mikrovlnných pulzů na qubit, prodloužili dobu, po kterou jejich qubity uchovávaly jejich kvantovou informaci (dobu koherence) až na neuvěřitelných 5 sekund.
Tyto pulzy oddělují qubit od zdrojů šumu a chyb rychlým převracením kvantového stavu. Každý pulz obnoví již částečně rozmazaný stav qubitu vymazáním poruch, ke kterým na něm došlo v důsledku dekoherence v době mezi jednotlivými pulzy.
Vědci se domnívají, že by měla být možná ještě delší koherence. Prodloužení koherenčního času má významný vliv na to, jak složitou operaci dokáže budoucí kvantový počítač zvládnout nebo jak malý signál dokáže kvantový senzor detekovat. Například tento nový rekordní čas znamená, že můžeme provést více než 100 milionů kvantových operací, než dojde k dekoherenci.
Rozluštěno: Jak funguje kvantový počítač. Zdroj: YT, Scietific American, 2021.
Schopnost provádět odečet jednotlivých laserových pulsů otevírá novou příležitost: Použití světla vyzařovaného z qubitů karbidu křemíku k vývoji budoucího kvantového internetu. Základní operace, jako je kvantové provázání, kde kvantový stav jednoho qubitu může být určen čtením stavu jiného qubitu, jsou nyní uskutečnitelné pro systémy založené na karbidu křemíku – materiálu běžně využívaném v elektronice.
Qubity vibrujících atomů
Dne 26. ledna 2022 publikovali fyzici z MITMIT – Massachusetts Institute of Technology, prestižní americká univerzita v massachusettském Cambridge. Univerzita byla založena Williamem Bartonem Rogersem v roce 1861. Skládá se z pěti škol a jedné koleje. Přestože jde o soukromou univerzitu, je podporována i státem. Spravuje livingstonskou část detektoru LIGO. v časopise Nature objev qubitů ve formě vibrujících párů atomů. Atomy udržují superpozici dvou vibračních stavů, ve kterých dvojice kmitá vzájemně proti sobě a zároveň se synchronizovaně kýve. Tím je udržována superpozice mezi stovkami vibrujících párů fermionů a dojde k vytvoření nového „kvantového registru“ nebo systému qubitů, který se zdá být robustním po relativně dlouhou dobu až 10 sekund.
Tým byl schopen řídit vibrační stavy fermionových párů použitím proměnlivého magnetického pole prostřednictvím efektu známého jako Feshbachova rezonanceFeshbachova rezonance – rezonance, která nastává, je-li pohybová energie srážejících se atomů rovna energii vázaného stavu (molekuly). Při rezonanci prudce roste účinný průřez srážky atomů v s stavu (stravu s nulovým momentem hybnosti) a roste pravděpodobnost vzniku molekuly.. „Je to jako začít se dvěma neinteragujícími kyvadly a použitím magnetického pole mezi nimi vytvořit pružinu modifikovatelné tuhosti a pomalu tlačit kyvadla od sebe“, říká Zwierlein.
Tímto způsobem bylo možné současně manipulovat s asi 400 fermionovými páry. Jako skupina si qubity udržovaly stav superpozice po dobu až 10 sekund, než se jednotlivé páry zhroutily do jednoho nebo druhého vibračního stavu. Existují způsoby, jak snížit bariéru mezi páry tak, aby se spojily, interagovaly a pak se znovu rozdělily asi na jednu milisekundu, což ukazuje jasnou cestu k dvouqubitové bráně, která je zapotřebí k vytvoření kvantového počítače.
* * *
Všechny bulletiny této série
- Mohou stroje nabýt vědomí? – Historický vývoj názorů na podstatu vědomí
- Mohou stroje nabýt vědomí? – Vědomí a kvantová gravitace
- Mohou stroje nabýt vědomí? – Kvantová teorie informace
- Mohou stroje nabýt vědomí? – Spintronika a kvantové počítače
- Mohou stroje nabýt vědomí? – Generátory vědomí
- Mohou stroje nabýt vědomí? – Další komponenty neuronálního cytoskeletu
- Mohou stroje nabýt vědomí? – Výpočet koherenční doby v biosystémech
- Mohou stroje nabýt vědomí? – Vysokoteplotní koherence v živých buňkách
- Mohou stroje nabýt vědomí? – Kvantové neurony
Za texty je zodpovědný autor
Odkazy
- Milan Odehnal: Supravodivost a jiné kvantové jevy, Academia, 1992
- Roger Penrose: Mikrosvět, makrosvět a lidská mysl; Mladá fronta, 1999
- Stanislaw Lem: Tajemství čínského pokoje; Mladá fronta, 1999
- L. Andrej, M. Bednář, M. Čerňanský, K. Král, J. Souček: Kvantová teleportace a kvantová informace, Československý časopis pro fyziku 50 (2000) 19–40
- Tom Stonier: Informace a vnitřní struktura vesmíru, BEN – Technická literatura, 2002
