|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Od mřížových modelů ke kvantové chromodynamice II
Petr Kulhánek
V AB 47/2009 jsme se zabývali mřížovými modely magnetických látek. Chování látky je simulováno za pomoci spinůSpin – vlastní (vnitřní) rotační moment částice souvisící s Lorentzovou symetrií. Pro částici v centrálním poli se přirozeným způsobem skládá s momentem hybnosti. Částice s nenulovým spinem se mohou chovat jako elementární magnetické dipóly μ, aniž by měly elektrický náboj. Takové částice reagují na vnější magnetická pole. (elementárních magnetických momentů) rozmístěných na pravidelné mříži. Sousední spiny/momenty spolu interagují podle předem zadaného předpisu. Takový postup je úspěšný například pro feromagnetikaFeromagnetikum – materiál, ve kterém je energeticky výhodné, aby sousední magnetické momenty měly shodný směr. Tyto látky, například železo, jsou schopné značné magnetizace ve vnějším magnetickém poli. Po odstranění magnetického pole si ponechávají permanentní magnetizaci, tj. zůstávají zmagnetizované i bez vnějšího magnetického pole. Typickým příkladem je krystalické železo, kobalt či oxid chromičitý CrO2., u kterých mohou vznikat Weissovy doményMagnetická doména – oblast elementárních magnetických dipólových momentů, které jsou uspořádány jednotným způsobem. Magnetické domény v materiálu vznikají při teplotách nižších, než je Curieova teplota. Při vyšších teplotách je uspořádání elementárních magnetů chaotické., vírové struktury a spinové vlny, nebo vysokoteplotní chaotická fáze. Uvedený popis je ale také vhodný pro mřížový plyn (částice plynu buď ve vrcholu mříže je, nebo není), antiferomagnetikaAntiferomagnetikum – systém spinů ve kterém je energeticky výhodné, aby sousední magnetické momenty měly různou hodnotu spinu (například opačný směr). Při nízkých teplotách se vytvářejí periodické struktury opačně orientovaných momentů. Příkladem antiferomagnetika může být supravodič URu2Si2, dále chróm, slitina železa a manganu nebo oxid niklu NiO., spinová sklaSpinové sklo – magnetický materiál, který má za nízkých teplot chaotickou orientaci magnetických momentů. Jejich uspořádání připomíná klasické sklo. Vazbová energie sousedních magnetických momentů se mění náhodně místo od místa. i další systémy. V dnešním pokračování se zaměříme na některé ryze kvantové aplikace mřížových modelů, tzv. kvantovou teorii na mříži.
|
QCD – Quantum Chromodynamics, kvantová chromodynamika, teorie silné interakce. Kvarky interagují prostřednictvím polních částic silné interakce – gluonů. Silnou interakcí drží pohromadě kvarky například v neutronech a protonech. Silná interakce je zodpovědná i za soudržnost atomového jádra. K typickým rysům silné interakce patří uvěznění kvarků a jejich asymptotická volnost na malých vzdálenostech. Nábojem silné interakce je „barva“, odsud název chromodynamika. Dosah silné interakce je přibližně 10−15 m. Kvarky – částice, ze kterých jsou tvořeny těžké částice s vnitřní strukturou (hadrony). Hadrony dělíme na baryony složené ze tří kvarků (například protony a neutrony) a na mezony tvořené kvarkem a antikvarkem (například piony). Kvarky se dělí do tří generací, první tvoří kvarky „d“ (down) a „u“ (up), druhou kvarky „s“ (strange) a „c“ (charm) a třetí kvarky „b“ (bottom nebo beauty) a „t“ (top nebo truth). Kvarky mají neceločíselné (třetinové a dvoutřetinové) elektrické náboje. Jsou také nositeli barevného náboje silné interakce. Gluony – intermediální (polní, výměnné) částice silné interakce, která působí na hadrony a je krátkého dosahu. Tato interakce spojuje kvarky v mezony a baryony, udržuje pohromadě neutrony a protony v atomovém jádře a způsobuje některé rychlé rozpady elementárních částic. Celkem známe 8 gluonů. Tyto polní částice jsou nositeli barevného náboje (náboje silného interakce). Tím se silná interakce odlišuje od elektromagnetické a slabé interakce. |
Hubbardův model
Ani bouřlivě se rozvíjející výpočetní technika neumožňuje simulace elektronových systémů s mnoha (například 1023) elektronyElektron – první objevená elementární částice. Je stabilní. Hmotnost má 9,1×10−31 kg a elektrický náboj 1,6×10−19 C. Elektron objevil sir Joseph John Thomson v roce 1897. Existenci antičástice k elektronu (pozitron) teoreticky předpověděl Paul Dirac v roce 1928 a objevil Carl Anderson v roce 1932.. V takových situacích se pokoušíme sledovaný systém rozumně zjednodušit. Natolik rozumně, aby ještě popisoval vlastnosti skutečné látky, kterou chceme zkoumat. Představme si, že elektrony mohou být lokalizovány jen v určitých místech, například ve vrcholech pravidelné mříže. Tak je tomu třeba v krystalických látkách, kde je elektron v blízkosti určitého iontu. Nicméně modely elektronů na mříži mají mnohem širší uplatnění a lze pomocí nich obecně modelovat systémy se silně korelovanými elektrony, například vysokoteplotní supravodičeSupravodivost – supravodivost objevil v roce 1911 Kamerlingh-Onnes, který zjistil, že při ochlazení rtuti pod teplotu 4,2 K dochází k prudkému poklesu elektrického odporu až na milióntinu původní hodnoty. Za tento objev obdržel v roce 1913 Nobelovu cenu za fyziku, ale ještě dlouho trvalo, než se podařilo vysvětlit, proč se elektrony v ochlazeném materiálu pohybují bez odporu..
K nejjednodušším modelům tohoto typu patří tzv. Hubbardův model. Elektrony jsou kreovány a anihilovány ve vrcholech mříže tak, aby jejich chování odpovídalo energii systému při dané teplotě. Energie systému se skládá ze dvou odlišných členů. První člen je dán interakcí nejbližších sousedů (součet přes všechny dvojice nejbližších vrcholů). Dva nejbližší sousedé <a,b> přispějí k celkové energii výrazem
E<a,b> = –t (c+a↑cb↑ + c+a↓cb↓ + c+b↑ca↑ + c+b↓ca↓).
Vazební konstanta této interakce je označena t, symbol c+ označuje kreaci elektronu se spinem ↑ nebo ↓ v daném vrcholu, symbol c anihilaci. Tento člen umožňuje „přeskakování“ či „tunelování“ elektronů z jednoho vrcholu mříže do druhého. Druhá část energie je součtem přes všechny vrcholy, každý vrchol přispěje k celkové energii výrazem
Ea = U na↑na↓.
Symbol n znamená počet jedinců se spinem ↑ nebo ↓ v daném vrcholu. Kladná vazební konstanta U znamená repulzi elektronůElektron – první objevená elementární částice. Je stabilní. Hmotnost má 9,1×10−31 kg a elektrický náboj 1,6×10−19 C. Elektron objevil sir Joseph John Thomson v roce 1897. Existenci antičástice k elektronu (pozitron) teoreticky předpověděl Paul Dirac v roce 1928 a objevil Carl Anderson v roce 1932. na malých vzdálenostech: Pokud je ve vrcholu jeden elektron se spinem ↑ a jeden elektron se spinem ↓, přispějí k celkové energetické bilanci kladnou hodnotou U, pokud je ve vrcholu jediný elektron, přispěje tento vrchol nulovou hodnotou. Za nízkých teplot jsou preferovány stavy s co možná nejnižší energií, tedy jediný elektron ve vrcholu mříže. Oba energetické členy znamenají v jistém smyslu párovou interakci. První člen se týká interakce elektronů ve dvou nejbližších vrcholech mříže. Druhý se týká interakce dvojice elektronů v jednom jediném vrcholu (Coulombická repulze). V reálných materiálech je podíl vazebních konstant U/t mezi 10 až 50.
Model navrhl anglický fyzik John Hubbard (1931–1980) v roce 1963 k popisu chování elektronů v pevných látkách. Pomocí Hubbardova modelu lze snadno simulovat přechod látky mezi vodivým a nevodivým stavem. Dnes se model využívá k popisu chování ultrachladných atomů zachycených v optické mřížiOptická mříž – pravidelně se střídající minima a maxima elektrického potenciálu, jež vznikla interferencí dvou nebo více laserových svazků.. Původní model byl navržen pro dva fermionyFermiony – částice, které mají poločíselný spin, vlnová funkce je antisymetrická, splňují Pauliho vylučovací princip a podléhají Fermiho–Diracovu statistickému rozdělení. Patří mezi ně všechny leptony, kvarky a baryony – například elektron, neutrino, proton a neutron. Při nízkých teplotách fermiony obsazují stavy postupně, až po tzv. Fermiho mez., později se objevila i bosonováBosony – částice, které mají celočíselný spin, symetrickou vlnovou funkci, nesplňují Pauliho vylučovací princip a podléhají Boseho-Einsteinově statistickému rozdělení. Například jsou to všechny skalární i vektorové mezony, fotony a gluony. Při nízkých teplotách se bosony mohou hromadit v základním stavu. varianta Hubbardova modelu a různé další užitečné modifikace. Modely se nemusí omezovat na pravoúhlou mříž, interakce nemusí probíhat jen mezi nejbližšími sousedy, ale například i mezi sousedy na úhlopříčce s vazební konstantou t', uvažují se modely v mnoha dimenzích, atd.
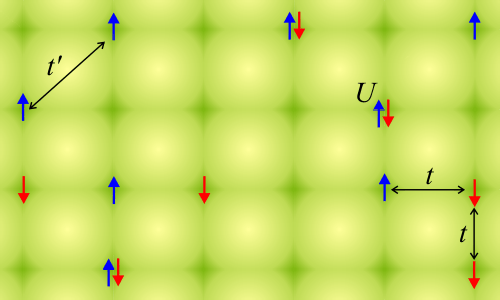
1. Hubbardův 2D model. Kresba autor.
V roce 1977 polský fyzik Jozef Špalek upravil Hubbardův model pro velké hodnoty interakční konstanty U do podoby se dvěma párovými interakcemi mezi nejbližšími vrcholy mříže. Model byl nazván podle označení vazebních konstant těchto interakcí jako tzv. t-J model. Člen s vazební konstantou t je podobný prvnímu členu Hubbardova modelu. Druhý člen s vazební konstantou J = 2t2/U obsahuje skalární součin dvou sousedních spinů, obdobně jako Heisenbergův model. Pomocí tohoto modelu se podařilo vysvětlit chování Mottových izolátorůMottův izolátor – skupina nevodivých materiálů, které by podle standardní pásové teorie měly být vodiči. Jev je způsoben párovými interakcemi elektron-elektron, které pásová teorie neuvažuje. Jev se vyskytuje za nízkých teplot například u NiO nebo CoO. Chování těchto látek vysvětlil až t-J model z roku 1977. včetně jejich feromagnetizmu. Později se t-J model stal úspěšným i při vysvětlení vysokoteplotní supravodivosti keramických materiálů, například La2−xSrxCuO4, kterou objevili Karl Allex Müller a Johannes George Bednorz v roce 1986.
Kvantová chromodynamika na mříži (LQCD)
Z teorie silné interakce, neboli kvantové chromodynamiky (QCDQCD – Quantum Chromodynamics, kvantová chromodynamika, teorie silné interakce. Kvarky interagují prostřednictvím polních částic silné interakce – gluonů. Silnou interakcí drží pohromadě kvarky například v neutronech a protonech. Silná interakce je zodpovědná i za soudržnost atomového jádra. K typickým rysům silné interakce patří uvěznění kvarků a jejich asymptotická volnost na malých vzdálenostech. Nábojem silné interakce je „barva“, odsud název chromodynamika. Dosah silné interakce je přibližně 10−15 m.), je velmi obtížné získávat předpovědi přímým výpočtem. U elektromagnetické interakce je energie vazby podstatně menší než klidová energie vázaných částic (například elektronuElektron – první objevená elementární částice. Je stabilní. Hmotnost má 9,1×10−31 kg a elektrický náboj 1,6×10−19 C. Elektron objevil sir Joseph John Thomson v roce 1897. Existenci antičástice k elektronu (pozitron) teoreticky předpověděl Paul Dirac v roce 1928 a objevil Carl Anderson v roce 1932. a protonuProton – částice složená ze tří kvarků (duu) se spinem 1/2, hmotností 1,673×10−27 kg (938 MeV) a elektrickým nábojem +1,6×10−19 C. Proton je na běžných časových škálách stabilní, pokud se rozpadá, je poločas rozpadu větší než 1035 let. Za objevitele protonu je považován Ernest Rutherford, který v roce 1911 objevil atomové jádro při analýze rozptylu částice alfa pronikající tenkou zlatou fólií. Samotná jádra vodíku (protony) detekoval v roce 1918 při ostřelování dusíku částicemi alfa. Antiproton byl objeven v roce 1955 Emilio Segrem a Owenem Chamberlainem. v atomu vodíkuVodík – Hydrogenium, je nejlehčí a nejjednodušší plynný chemický prvek, tvořící převážnou část hmoty ve vesmíru. Má široké praktické využití jako zdroj energie, redukční činidlo při chemické syntéze a v metalurgii nebo jako náplň balonů a vzducholodí. Vodík objevil roku 1766 Henry Cavendish.). U silné interakce je tomu naopak. Energie vazby tří kvarkůKvarky – částice, ze kterých jsou tvořeny těžké částice s vnitřní strukturou (hadrony). Hadrony dělíme na baryony složené ze tří kvarků (například protony a neutrony) a na mezony tvořené kvarkem a antikvarkem (například piony). Kvarky se dělí do tří generací, první tvoří kvarky „d“ (down) a „u“ (up), druhou kvarky „s“ (strange) a „c“ (charm) a třetí kvarky „b“ (bottom nebo beauty) a „t“ (top nebo truth). Kvarky mají neceločíselné (třetinové a dvoutřetinové) elektrické náboje. Jsou také nositeli barevného náboje silné interakce. v protonu je podstatně větší než hmotnosti jednotlivých kvarků. Standardní poruchová teorie (rozvoj řešení do řad) u silné interakce selhává. Se vzdáleností kvarků jejich vzájemné silové působení neubývá, jak tomu je u elektromagnetické interakce, ale naopak roste. To vede k uvěznění kvarků do oblasti o rozměrech 10–15 m a selhání poruchového přístupu. Za běžných podmínek není možné získat volný, nevázaný kvark.
Jednou z možností, jak získávat současnými výpočetními prostředky předpovědi z kvantové chromodynamikyQCD – Quantum Chromodynamics, kvantová chromodynamika, teorie silné interakce. Kvarky interagují prostřednictvím polních částic silné interakce – gluonů. Silnou interakcí drží pohromadě kvarky například v neutronech a protonech. Silná interakce je zodpovědná i za soudržnost atomového jádra. K typickým rysům silné interakce patří uvěznění kvarků a jejich asymptotická volnost na malých vzdálenostech. Nábojem silné interakce je „barva“, odsud název chromodynamika. Dosah silné interakce je přibližně 10−15 m. je řešení problému neporuchovým přístupem, například na mříži. KvarkyKvarky – částice, ze kterých jsou tvořeny těžké částice s vnitřní strukturou (hadrony). Hadrony dělíme na baryony složené ze tří kvarků (například protony a neutrony) a na mezony tvořené kvarkem a antikvarkem (například piony). Kvarky se dělí do tří generací, první tvoří kvarky „d“ (down) a „u“ (up), druhou kvarky „s“ (strange) a „c“ (charm) a třetí kvarky „b“ (bottom nebo beauty) a „t“ (top nebo truth). Kvarky mají neceločíselné (třetinové a dvoutřetinové) elektrické náboje. Jsou také nositeli barevného náboje silné interakce. a gluonyGluony – intermediální (polní, výměnné) částice silné interakce, která působí na hadrony a je krátkého dosahu. Tato interakce spojuje kvarky v mezony a baryony, udržuje pohromadě neutrony a protony v atomovém jádře a způsobuje některé rychlé rozpady elementárních částic. Celkem známe 8 gluonů. Tyto polní částice jsou nositeli barevného náboje (náboje silného interakce). Tím se silná interakce odlišuje od elektromagnetické a slabé interakce. jsou lokalizovány ve vrcholech prostorové mříže a mohou se přemisťovat jen podél spojnic. Takové metody se nazývají LQCD (Latice Quantum ChromoDynamics) a jsou v mnohém podobné mřížovým modelům feromagnetikFeromagnetikum – materiál, ve kterém je energeticky výhodné, aby sousední magnetické momenty měly shodný směr. Tyto látky, například železo, jsou schopné značné magnetizace ve vnějším magnetickém poli. Po odstranění magnetického pole si ponechávají permanentní magnetizaci, tj. zůstávají zmagnetizované i bez vnějšího magnetického pole. Typickým příkladem je krystalické železo, kobalt či oxid chromičitý CrO2., kterými jsme se zabývali doposud. Přímými předchůdci LQCD jsou Hubbardův model a t-J model.
Čím menší je rozestup vrcholů, tím více se výsledky přibližují skutečnému kontinuu. Často se provádějí výpočty s různou velikostí mříže a výsledky se extrapolují k nulové vzdálenosti vrcholů mříže. Pro částice lokalizované na mříži může maximální hybnost nabývat hodnotu p ~ ħ/a, kde a je mřížková konstanta (vzdálenost vrcholů). Plyne to z Heisenbergových relací neurčitosti. V mřížových modelech jsou tak přirozeným způsobem oříznuty nekonečné hodnoty, které se vyskytují v kvantové chromodynamice na časoprostorovém kontinuu a obtížně se odstraňují pomocí renormalizaceRenormalizace – matematická procedura vedoucí k odstranění některých nekonečen vyskytujících se v kvantové teorii.. I přes podstatné zjednodušení znamená LQCD výpočty na samé hranici možností dnešních superpočítačů. Výpočty se provádějí pro nerealisticky veliké hmotnosti kvarků. Lehké kvarky mají totiž velkou korelační délku (jsou korelovány i se vzdálenými sousedy) a takové výpočty vyžadují příliš rozsáhlé mříže.
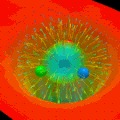
Pomocí LQCD byl zkoumán fázový přechod mezi uvězněnými kvarky a kvarkovým-gluonovým plazmatemQGP – kvarkové-gluonové plazma. Podaří-li se nám „dostat“ kvarky na vzdálenosti menší než 10−15 m, začnou se kvarky a gluony chovat jako volné (nevázané) částice. Tím vznikne zcela zvláštní stav hmoty nazývaný kvarkové-gluonové plazma. Poprvé byla tato fáze látky připravena na urychlovači SPS ve středisku CERN v roce 2000. Ve vesmíru existovalo QGP v období do 10 mikrosekund po vzniku vesmíru.. Právě z výpočtů pomocí LQCD vyplynulo, že tento přechod probíhá při energii 170 MeVElektronvolt – jednotka energie. Jde o energii, kterou získá elektron urychlením v potenciálovém rozdílu jeden volt, 1 eV = 1,6×10−19 J. V jaderné fyzice se používají spíše větší násobky této jednotky, kiloelektronvolt keV (103 eV), megaelektronvolt MeV (106 eV), gigaelektronvolt GeV (109 eV), teraelektronvolt TeV (1012 eV) nebo petaelektronvolt PeV (1015 eV). V těchto jednotkách se také vyjadřuje hmotnost (E=mc2) a teplota (E=kBT). Jeden elektronvolt odpovídá teplotě přibližně 11 600 K. na částici. Tomu odpovídá teplota řádově 2×1012 K, tedy cca stotisíckrát vyšší teplota, než je v nitru SlunceSlunce – nám nejbližší hvězda, tzv. hvězda hlavní posloupnosti, která se nachází ve vzdálenosti 149,6×106 km od Země. Jde o žhavou plazmatickou kouli s průměrem 1,392×106 km, teplotou na povrchu 5 780 K, teplotou v centru přibližně 15×106 K a zářivým výkonem 3,846×1026 W. Zdrojem energie je jaderná syntéza, při které se za každou sekundu sloučí v jádru Slunce 700 milionů tun vodíku na hélium.. Obdobných podmínek se podařilo dosáhnout po šesti letech experimentů v roce 2000 na urychlovači SPSSPS – Super Proton Synchrotron, jeden z urychlovačů v Evropském středisku jaderného výzkumu CERN. Dosažitelná energie je 400 GeV/proton. Urychlovač je v provozu od roku 1976. Na přelomu roku 1983 a 1984 zde byly objeveny polní bosony slabé interakce a v roce 2000 zde bylo poprvé připraveno kvarkové-gluonové plazma (zárodečná polévka, ze které vznikal vesmír). ve středisku CERNCERN – Conseil Européen pour la Recherche Nucléaire, Evropské centrum jaderného výzkumu. Komplex urychlovačů a laboratoří na pomezí Švýcarska a Francie založený v roce 1954. Na výzkumu se podílí 22 členských zemí včetně České republiky. K největším objevům patří detekce polních částic slabé interakce, příprava antivodíku a vytvoření kvarkového-gluonového plazmatu, pralátky, z níž vznikal vesmír. V současné době je zde vybudován největší urychlovač světa – Large Hadron Collider, který byl po závadě na jednom z magnetů opětovně spuštěn na konci roku 2009. V roce 2012 byl na LHC objeven Higgsův boson, poslední částice standardního modelu. V CERNu byl také vynalezen a poprvé použit Web., kde bylo objeveno kvarkové-gluonové plazma. LQCD se dnes využívá při simulaci uvěznění kvarků, v teorii strun, při hledání axionů i v mnoha dalších aplikacích.

2. LQCD počítačová simulace nitra protonu. Mříž není zobrazena. Červená, zelená a modrá kulička znázorňují kvarky v protonu. Ostatní oblasti jsou gluonová pole (97 % hmotnosti protonu). Zelený a fialový objekt znázorňují excitaci gluonového pole – pár kvark-antikvark. Z výpočtů se sestavují celé animace, jednu z nich si prohlédněte v dnešní Animaci týdne (tam byla pro názornost ponechána výpočetní mříž). Zdroj: Derek B. Leinweber, University of Adelaide.
Spinový žebřík a uvěznění kvarků
Uvěznění kvarků v mezonuMezon – částice složená z jednoho kvarku a jednoho antikvarku. Název vznikl z toho, že první objevené mezony měly hmotnost „mezi“ hmotností elektronu a protonu. Pokud se kvarky složí s nesouhlasným spinem, vznikne skalární mezon (má nulový spin), pokud se souhlasným spinem vznikne vektorový mezon (spin má roven jedné). Skalární mezony zkombinované z kvarků „d“ a „u“ nazýváme piony, vektorové róony. Pokud mezon obsahuje kvark „s“, nazývá se kaon. nebo baryonuBaryon – elementární částice složená ze tří kvarků s různým barevným nábojem. Výsledná barva je „bílá“. Baryony podléhají silné interakci a patří proto mezi hadrony. Baryony složené z kvarků první generace (d, u) dělíme na nukleony se spinem rovným 1/2 (proton a neutron) a delta baryony se spinem rovným 3/2 (4 částice s různým nábojem). Baryony obsahující s kvark nazýváme hyperony. Nejznámějším je lambda hyperon. Hyperony byly hojně zastoupené v raných vývojových fázích vesmíru, často hovoříme o hyperonovém plynu. Dnes vznikají interakcí kosmického záření s horními vrstvami atmosféry a umíme je vytvořit uměle na urychlovačích. je zatím chápáno jen rámcově. Není například jasné, jakou hmotnost budou mít lehčí mezony, na které se rozpadá mezon těžší (když dojde k „přetržení“ gluonové niti). Proto může být užitečné zkoumat podobně uvězněné systémy jiného charakteru. Na konci roku 2009 byl pozorován obdobný jev v tzv. spinových žebřících. Popišme si tento objev podrobněji.
Začněme s jednorozměrným řetězcem antiferomagnetikaAntiferomagnetikum – systém spinů ve kterém je energeticky výhodné, aby sousední magnetické momenty měly různou hodnotu spinu (například opačný směr). Při nízkých teplotách se vytvářejí periodické struktury opačně orientovaných momentů. Příkladem antiferomagnetika může být supravodič URu2Si2, dále chróm, slitina železa a manganu nebo oxid niklu NiO. (obr. 3). V základním stavu jsou sousední spiny seřazeny antiparalelně (opačně orientované spiny přispějí k energii nižší hodnotou než souhlasně orientované spiny). Základní stavy (stavy s nejnižší možnou energií) existují dva (liší se orientací spinů) a při extrémně nízké teplotě dojde k narušení symetrie a výběru jednoho ze dvou základních stavů.

3. Základní stav antoferomagnetického řetězce. Podle [7].
Zvýšíme-li nyní teplotu, dojde ke zvýšení energie řetězce. Díky teplotním fluktuacím se objeví oblast obrácených spinů (na obr. 4 je vyznačena červeně). Jde vlastně o část druhého základního stavu, která je vnořena do již existujícího základního stavu. Obrácená oblast je od okolí oddělena tzv. doménovými stěnami (A, B) neboli spinony. Doménová stěna (spinon) je tvořena dvojicí stejně orientovaných spinů, které jsou nositeli teplotní fluktuace (souhlasně orientované spiny mají vyšší energii než nesouhlasně). Takové excitace (spinony) se vždy objevují po dvojicích, jsou nositeli nevykompenzovaného spinu (1/2) v řetězci a celková energie řetězce nezávisí na vzdálenosti obou spinonů. Pohyb spinonu podél řetězce nemění celkovou energii řetězce. Spinon se chová jako volná kvazičástice, která není nijak korelována s druhým spinonem. Oba současně vzniklé spinony nejsou nijak vázané.

4. Dvojice doménových stěn (spinonů). Podle [7].
Uvažujme nyní dva antiferomagneticky provázané řetězce spinů, tzv. spinový žebřík. Jeden ze dvou základních stavů žebříku je na obr. 5. Pokud nyní zvýšíme teplotu, objeví se v jednom z řetězců opět teplotní fluktuace – oblast obrácených spinů ohraničená dvěma spinony (doménovými stěnami). Situace je ale nyní velmi odlišná. Oblast obrácených spinů má shodný směr se spiny sousedního řetězce a celá oblast tak přispívá ke zvýšení energie žebříku. Čím větší je vzdálenost spinonů A a B (doménových stěn), tím vyšší je energie spinového žebříku. Oba spinony jsou nyní silně vázané a energie jejich vazby roste s jejich vzdáleností! Situace je obdobná dvojici kvarku a antikvarku uvězněné v mezonu. Zde také roste energie vazby se vzdáleností kvarků, což kvarkům neumožňuje uniknout z vázaného stavu. Ani v žebříku se jeden spinon nemůže vzdálit od druhého. Existuje zde i další paralela. Kvarky mají neceločíselný náboj a teprve jejich vázané stavy se navenek jeví tak, jakoby měly celočíselný náboj. Obdobně je každý spinon nositelem nevykompenzovaného spinu (1/2) a teprve dvojice vázaných spinonů má celočíselný spin.
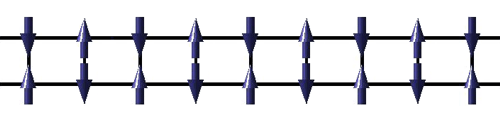
Základní stav spinového žebříku. Podle [7].

Excitovaný stav spinového žebříku. Podle [7].
Kvantové žebříky je možné snadno numericky simulovat a zjišťovat tak vlastnosti uvězněných jedinců. Důležité je, že na sklonku roku 2009 Bella Lake z Helmholtzova centra v Berlíně pozoroval se spolupracovníky uvězněné stavy dvou spinonů ve spinovém žebříku i experimentálně. Jednalo se o oxid CaCu2O3. Materiál byl zkoumán za pomoci ohybu neutronů. Při vysokých energiích byly patrné samostatné lineární řetězce s dvojicemi nevázaných spinonů. Při nízkých energiích došlo ke spárování řetězců do spinových žebříků a spinony začaly být vázané obdobným způsobem jako kvarky v baryonech. Mezi spinony ve spinových žebřících a kvarkyKvarky – částice, ze kterých jsou tvořeny těžké částice s vnitřní strukturou (hadrony). Hadrony dělíme na baryony složené ze tří kvarků (například protony a neutrony) a na mezony tvořené kvarkem a antikvarkem (například piony). Kvarky se dělí do tří generací, první tvoří kvarky „d“ (down) a „u“ (up), druhou kvarky „s“ (strange) a „c“ (charm) a třetí kvarky „b“ (bottom nebo beauty) a „t“ (top nebo truth). Kvarky mají neceločíselné (třetinové a dvoutřetinové) elektrické náboje. Jsou také nositeli barevného náboje silné interakce. samozřejmě existuje mnoho rozdílů. Nicméně otevírá se zde mimořádně zajímavá možnost numerických simulací a přímých experimentů s uvězněnými spinony, která může objasnit zatím nevyřešené otázky kvantové chromodynamikyQCD – Quantum Chromodynamics, kvantová chromodynamika, teorie silné interakce. Kvarky interagují prostřednictvím polních částic silné interakce – gluonů. Silnou interakcí drží pohromadě kvarky například v neutronech a protonech. Silná interakce je zodpovědná i za soudržnost atomového jádra. K typickým rysům silné interakce patří uvěznění kvarků a jejich asymptotická volnost na malých vzdálenostech. Nábojem silné interakce je „barva“, odsud název chromodynamika. Dosah silné interakce je přibližně 10−15 m..
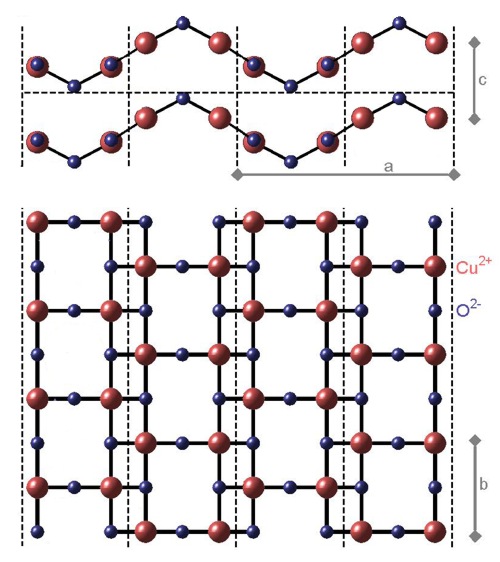
Schéma spinového žebříku CaCu2O3. Nahoře je pohled
z boku, dole pohled shora.
Vzdálenost a je
0,9949 nm, b je 0,4078 nm
a c je 0,3460 nm. Ionty Cu2+ mají
spin 1/2 a jsou vyznačeny červeně.
Podle [7].
Konec
Klip týdne: Kvantová chromodynamika na mříži
Kvantová chromodynamika na mříži. Kvantová chromodynamika (QCD) je současnou teorií silné interakce. Standardní metody výpočtu, jako je například poruchová teorie, u QCD selhávají. Jednou z alternativ je diskretizace prostoru a výpočty na mříži, v jejíž vrcholech jsou lokalizovány kvarky a gluonová pole. V první animaci vidíte typickou časoprostorovou strukturu gluonového pole. Výpočetní oblast má rozměry 2,4×2,4×3,6 fm. Znázorněna je hustota energie gluonového pole. Tuto animaci promítal F. Wilczek při převzetí Nobelovy ceny za teorii silné interakce v roce 2004. V druhé animaci je znázorněna vazba kvarku a antikvarku v mezonu, tzv. gluonová nit. Vzdálenost kvarků se mění od 0,125 fm do 2,25 fm (1,3-násobek průměru protonu). Povšimněte si, že průměr gluonové niti se nemění. Prohnutá plocha představuje hustotu energie v rovině procházející středy páru kvark-antikvark. Vektorové pole zobrazuje gradient hustoty energie. V poslední animaci je stejným způsobem znázorněna vazba tří kvarků v baryonu. Zdroj: Derek B. Leinweber, University of Adelaide. (gif, 3 MB) (gif, 3 MB) (gif, 2 MB)
Literatura