Měření vzdáleností

Měření vzdáleností se na Zemi zdá být poměrně jednoduchou naukou. Nejjednodušeji lze postupovat tak, že k úseku neznámé délky přikládáme pravítko známé velikosti a poměřováním obou vzdálenost odměříme. Lidé už ve starověku postupně vymysleli metody, které nevyžadují přímé přikládání měřítka. Objekt, jehož vzdálenost chceme změřit, už nemusí být nutně fyzicky přímo dostupný. Při takovém měření lze využít znalosti geometrie a nedostupnou vzdálenost nahradit měřením úhlů. V geodézii a kartografii se metody založené na přesném zjišťování úhlů ve vhodně zvolených trojúhelnících – odtud trigonometrie – používají úspěšně dodnes. Vzdálenost či rozměry nedostupných staveb nebo přírodních útvarů se proto zjišťují pomocí úhlů měřených z různých míst. Dochází tak ke změně úhlů, pod kterými pozorovaný objekt sledujeme. Této změně se říká paralaxa. Ke zjištění hledané veličiny je nutné, krom změřených pozorovacích úhlů, znát také vzdálenost mezi jednotlivými pozorovacími stanovišti.

Některé klasické úlohy starých geometrů. Zdroj: J. Hons, B. Šimák: Pojďte s námi
měřit zeměkouli – Papírová zeměkoule; nakl. Dr. Karoliny Kolářové, Praha, 1942.

Měření blízkých vzdáleností, paralaxa

Nebeská tělesa nejsou, stejně tak jako například tvrz na ostrově či loď na moři, přímo dostupná. Je proto přirozené, že se astronomové pokoušeli o něco podobného jako kartografové pozemní a vycházeli z jimi vyvinutých metod. V dobách, kdy ještě nebyl objeven dalekohled, byly zhotovovány mapy oblohy sloužící především pro námořní navigaci. Polohy jednotlivých hvězd byly určovány nejrůznějšími úhloměry, které byly také postupně zdokonalovány, díky čemuž docházelo ke zpřesňování hvězdných map.

Ze starověku je známý kartografický čin Eratosthéna, kterému se podařilo pomocí paralaxy Slunce změřit velikost Země. Musel ale přitom vycházet z do té doby obtížně ověřitelného předpokladu, že je Země kulatá. Teprve potom měl jeho experiment smysl a vypovídal o tom, jak je zemská koule veliká. Při prvých pokusech nebeských kartografů zjišťovat polohy nebeských objektů se tito museli vypořádat se skutečností, že vzdálenosti zjišťují z povrchu zeměkoule, která je poměrně velká a že to může mít vliv na výsledky jejich měření. Polohu hvězdy lze určit dvěma souřadnicemi: výškou nad obzorem a azimutem. Tyto souřadnice ale budou mít nepatrně odlišné hodnoty, budeme-li je zjišťovat z místa na povrchu Země (topocentricky), nebo z jejího středu (geocentricky). Jelikož se obloha nad pozorovatelem v průběhu dne a noci otáčí, největší rozdíl – denní paralaxa – mezi těmito hodnotami nastává, je-li hvězda právě na obzoru. Nachází-li se hvězda v nadhlavníku, je denní paralaxa nulová. V určování souřadnic je proto nutno důsledně odlišovat souřadnice topocentrické, které jsou dostačující pro jednoho pozorovatele a souřadnice geocentrické. Geocentrické souřadnice jsou přepočítávány na střed Země a pro více pozorovatelů v různých místech na Zemi se nemění. Jejich pozorování tak lze vzájemně porovnávat.

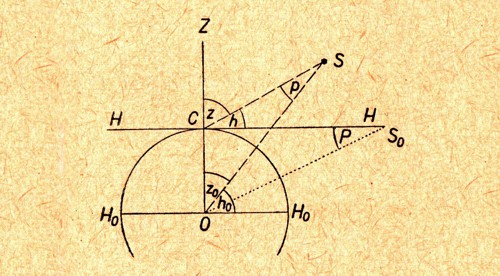
Denní paralaxa. C je místo pozorovatele na povrchu zeměkoule, H je jeho horizont. H₀ je horizont hypotetického pozorovatele usazeného ve středu Země. Z je zenit, S je obecná hvězda a p je paralaxa. Souřadnice hvězdy pak jsou z, z₀ (zenitová vzdálenost), h, h₀ (výška nad obzorem). Zdroj: Jaroslav Široký, Miroslava Široká: Základy astronomie v příkladech; SPN v Praze, 1977.

Denní paralaxu lze pro nebeskou kartografii využít na malé vzdálenosti srovnatelné s velikostí Země tak, že ji budeme měřit pro stejný objekt, třeba Měsíc nebo kometu, z rozdílných míst. Pokud známe velikost Země, můžeme dopočítat vzdálenost. Denní paralaxu komety z roku 1472 se pokusil změřit Regiomontanus. Jakubovou holí určil hodnotu 6°, což je ve srovnání s paralaxou Měsíce číslo velké, a proto kometyKometa – těleso malých rozměrů obíhající kolem Slunce většinou po protažené eliptické dráze s periodou od několika let po tisíce roků. Při přiblížení ke Slunci se vypařuje část materiálu jádra a kometa vytváří komu a eventuálně ohon. Jde o pozůstatky materiálu z doby tvorby sluneční soustavy. Dnes se nacházejí v Oortově oblaku za hranicemi sluneční soustavy, ve vzdálenosti 20 000÷100 000 au. Některé komety pocházejí i z bližšího Kuiperova pásu. dál zůstávaly v sublunární sféře, kam je umístil jako neshořelé zemské výpary Aristotelés. V roce 1572 se v souhvězdí Kasiopeji objevila nová hvězda. Paralaxu této supernovySupernova – rozmetání podstatné části hvězdy, při kterém vznikne extrémně jasný objekt, jehož svítívost se o více než 4 řády zvýší. Minimálně 10 % hmotnosti původní hvězdy se přemění na energii exploze. Svítivost posléze klesá v průběhu týdnů či měsíců. K tomuto konci vedou dvě možné cesty: 1) jedná se o velmi hmotnou hvězdu, která ve svém jádře vyčerpala zásoby paliva a začala se hroutit pod silou své vlastní gravitace na neutronovou hvězdu, nebo černou díru; 2) jedná se o bílého trpaslíka, který nahromadil materiál od svého hvězdného průvodce, dosáhl Chandrasekharovy meze a prodělal objemovou termonukleární explozi., známé jako Tychonova hvězda, se pokoušelo určit mnoho hvězdářů, ale nikomu se to nepodařilo. Dostupná jsou měření Tychonova, Tadeáše Hájka z Hájku, Cornelia Gemmy, Bartoloměje Reisachera a Keplerova učitele Mästlina. V té době již bylo zřejmé, že denní paralaxu Měsíce změřit lze, i když výsledky byly dosti rozdílné. Výsledkem nezměřitelnosti paralaxy úkazu z roku 1572 proto bylo, že nově se objevivší hvězda se nutně musí nacházet mnohem dále než Měsíc. Roku 1752 změřili Jérôme Lalande (ten, který zavedl do hvězdného nebe roku 1799 souhvězdí Kočky – Felis) v Berlíně a Nicolas-Louis de Lacaille na Mysu Dobré naděje současně zenitovou vzdálenost Měsíce a určili tak vzdálenost Měsíce od středu Země na 58,8 zemských poloměrů. Skutečnost, že průměrná vzdálenost je 60,27 R_Z, je důkazem použitelnosti této metody.

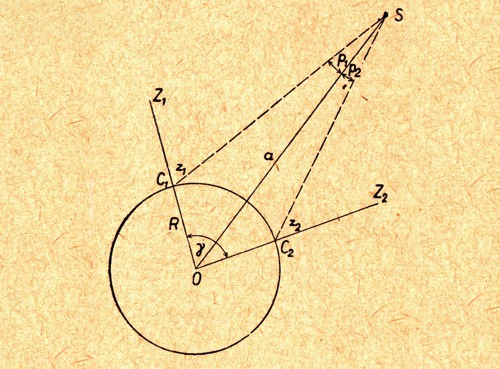
Horizontální paralaxa pro dvě pozorovací místa a určení vzdálenosti hvězdy S. Při znalosti vzájemných poloh obou pozorovacích míst C₁ a C₂ a velikosti Země lze změřením zenitových vzdáleností z₁ a z₂ určit pro poměrně blízké objekty vzdálenost od středu Země O ke sledované hvězdě S. Zdroj: Jaroslav Široký, Miroslava Široká: Základy astronomie v příkladech; SPN v Praze, 1977.

Roku 1717 se Edmondu Halleyovi při porovnávání jeho měření hvězdných poloh s katalogy Flamsteedovým a Tychonovým a ještě se staršími katalogy podařilo objevit vlastní pohyb hvězd. Aldebaran, Sírius, Arkturus a Betelgeuse jevily patrné změny polohy, které nebylo možno vysvětlit nepřesností předchozích měření. Roku 1760 Tobias Mayer pak nalezl vlastní pohyb již u 57 hvězd. Logicky se v té době hledala metoda, jak zjistit vzdálenost hvězd, jejichž vlastní pohyb byl největší a které by proto mohly být hvězdami velmi blízkými. Analogií s denní paralaxou se nabízela paralaxa ročníParalaxa – úhlový rozměr velké poloosy elipsy, kterou hvězda zdánlivě opisuje na obloze vzhledem ke vzdálenějším objektům. Tento zdánlivý pohyb blízkých hvězd je způsoben pohybem Země kolem Slunce (na hvězdu se díváme odjinud v létě a odjinud v zimě). Čím je hvězda blíže, tím je její paralaxa větší. Největší je u Proximy Centaury, kde činí 0,76″., jejíž základnu tvoří průměr zemské dráhy okolo Slunce. Úspěch se dostavil až na přelomu 18. a 19. století. Friedrich Wilhelm Bessel v Královci ověřil roku 1812 neobvykle velký vlastní pohyb hvězdy 5. velikosti označené 61 Cygni objevený Piazzim. Poté, co byl roku 1829 v Královci instalován nový Fraunhoferův heliometr, Bessel soustavně měřil hvězdu 61 Labutě a v roce 1838 publikoval změření prvé roční paralaxy: 0,314“. Hvězda byla vzdálena 600 000krát dále než Slunce, což byla zřejmě jedna z hvězd nejbližších. Friedrich Georg Wilhelm von Struve publikoval v roce 1840 měření paralaxy Vegy provedené na nové Pulkovské hvězdárně u Petrohradu a jím provedené měření se liší od dnes udávané hodnoty zhruba dvakrát. Třetím šťastlivcem byl Thomas Henderson, který na hvězdárně na Mysu Dobré naděje v roce 1838 změřil paralaxu jasné hvězdy 1. velikosti α Centauri. Jím udaná hodnota byla sice nesprávná (1“), ale ke skutečné hodnotě 0,754“ neměla daleko. Astronomům začalo být postupně jasné, že měření vzdáleností je poměrně citlivá disciplína vyžadující nejen trpělivost, ale hlavně ty nejlepší přístroje a že hvězdy jsou mnohem dál, než si do té doby kdo dokázal představit.

Měření blízkých vzdáleností. Kresba Ivan Havlíček.

Měření paralaxy pomocí tranzitu vnitřních planet

K proměřování Sluneční soustavy bylo zapotřebí určit vzdálenost Země od Slunce. Edmond Halley navrhl měření přechodu MerkuruMerkur – planeta nejbližší Slunci. Je to skalnatá planeta, posetá krátery podobně jako náš Měsíc. Jde o nejmenší planetu vůbec. Je téměř bez atmosféry. Teplota povrchu tohoto tělesa kolísá mezi −180 °C a 430 °C. Merkur se otočí kolem vlastní osy jednou za 59 našich dní. Jeho doba oběhu kolem Slunce trvá 88 dní. Jde o příklad vázané rotace (spinorbitální interakce) v poměru 2:3 způsobené slapovými silami. Dráha Merkuru kolem Slunce je protáhlá elipsa, která se stáčí vlivem přítomnosti ostatních planet. Malá část stáčení perihelia dráhy (43″ za století) je způsobena efekty obecné relativity. nebo VenušeVenuše – nejbližší planeta vzhledem k Zemi. Hustá atmosféra zabraňuje přímému pozorování povrchu. Díky skleníkovému efektu je na povrchu vysoká teplota, nejvyšší dosud naměřená hodnota činí 480 °C. Venuše obíhá kolem Slunce takřka po kruhové dráze ve vzdálenosti 108 milionů kilometrů s periodou 225 dní. Otočení kolem vlastní osy (proti oběhu, tzv. retrográdní rotace) trvá 243 pozemských dnů. To znamená, že na Venuši Slunce vychází a zapadá jen dvakrát za jeden oblet Slunce. Oblaka Venuše dobře odrážejí sluneční svit a proto je tato planeta po Slunci a Měsíci nejjasnějším tělesem na obloze. Na večerní obloze jí můžeme spatřit jako Večernici a na ranní obloze jako Jitřenku. přes sluneční kotouč, při němž lze zjistit přesnou hodnotu sluneční paralaxy nikoli přímým geometrickým měřením, ale měřením času. Zjistit dobu trvání přechodu pozorovaného z různých míst na Zemi se zdálo být snazší než určování paralaxy Slunce, které je úhlově velké a pro přímé měření přesné geocentrické polohy na obloze příliš jasné. Úspěch Halleyem navržené metody se dostavil až v letech 1822 – 1824, kdy Johann Franz Encke publikoval analýzy mnoha předchozích měření a určil sluneční paralaxu na 8,57“, z níž vycházela střední vzdálenost ke Slunci na 153 milionů kilometrů. Poprvé bylo možné Sluneční soustavu „kalibrovat“ a určit vzdálenosti mezi slunečními oběžnicemi nejen v poměrných vztazích, ale v absolutních číslech, tedy v kilometrech. V současnosti lze použít rádiových měření, jejichž přesnost je v jednotkách kilometrů. Na Měsíci jsou od dob programu ApolloApollo – americký program pilotovaných vesmírných letů probíhající v letech 1961 až 1972 a současně název kosmické lodi, která dopravila člověka na Měsíc. Vyvrcholením bylo přistání člověka na Měsíci (Apollo 11, Neil Armstrong, 20. 7. 1969). K cestě na Měsíc byla používána dosud největší nosná raketa Saturn V. Astronauté posledních misí využívali k pohybu po povrchu Měsíce speciální motorové vozítko. umístěny optické koutové odrážeče, s jejichž pomocí lze vzdálenost k Měsíci měřit laserem s přesností na centimetry.

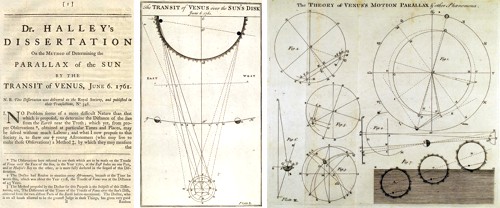
Metoda měření sluneční paralaxy popsaná Halleyem v roce 1716 prostřednictvím
 měření transitu Venuše v roce 1761. Zdroj: MHS.

Obecně lze pomocí paralaxy měřit za pomoci konečné velikosti zemské dráhy vzdálenosti do několika stovek světelných roků. Jde o trigonometrickou a současně nejpřesnější možnou metodu měření vzdáleností ve vesmíru. Z metody je odvozena jednotka vzdálenosti nazývaná parsek – vzdálenost, ze které je poloměr zemské dráhy okolo Slunce pozorovatelný pod úhlem jedné obloukové vteřiny. Úhlová měření jsme schopni ze Země provádět s přesností na setiny, nanejvýš tisíciny úhlových vteřin, záleží na charakteristikách pozorovaného jevu. Tedy vzdálenosti takto určené budou řádově ve stovkách parsekůParsek – pc, paralaktická sekunda, astronomická jednotka vzdálenosti. Jde o vzdálenost, ze které je vidět střední vzdálenost Země-Slunce (jedna astronomická jednotka) pod úhlem jedné obloukové vteřiny. Měří se kolmo k zornému paprsku. Číselně je 1 pc = 30×10¹² km, což je zhruba 3,26 světelného roku. Často používanými násobky jsou kiloparsek (kpc) a megaparsek (Mpc).. Dejte si pozor na používání správných pojmů: jednotkou času je sekunda a jednotkou velikosti úhlu je vteřina.

Měření středních vzdáleností, metoda cefeid

Pokud se ve vesmíru cokoliv nachází ve větší vzdálenosti než několik stovek světelných roků, tak pro zjištění vzdálenosti bude nutno použít jiné metody. Hvězdy sice ještě stále vidět jsou, ale jejich pohyby jsou už metodami založenými na geometrii neměřitelné. Možnost se nabídla na konci 18. století objevením pulzujících proměnných hvězd pojmenovaných cefeidyCefeidy – proměnné hvězdy se známou závislostí perioda/svítivost, využívají se při odhadech vzdáleností. Pojmenovány jsou podle hvězdy δ Cephei, jejíž proměnnost objevil John Goodricke (1764–1786). K určování vzdáleností využila tento typ proměnných hvězd poprvé Henrietta Swan Leavittová (1868–1921) v roce 1912. podle hvězdy δ Cephei, jejíž proměnnost byla objevena v roce 1784. Jde o hvězdy, které pravidelně mění svoji svítivost. Cefeidy mají poměrně vysokou svítivost, pravidelný průběh světelné křivky je provázen periodickou změnou teploty atmosféry – spektrálního typu, a konečně změnou poloměru. Jelikož střední hustota je závislá na hmotnosti, musí existovat vztah mezi periodou pulzů a svítivostí hvězdy. Tuto závislost empiricky objevila Henrietta Swan Leavittová v roce 1912, když proměřovala proměnné hvězdy ve Velkém Magellanově oblakuLMC – Large Magellanic Cloud, Velké Magellanovo mračno. Trpasličí souputník naší Galaxie ve vzdálenosti 180 000 l.y. Jde o nádherný objekt viditelný spolu s Malým Magellanovým mračnem na jižní obloze.. Pokud změříme periodu pulzací a zdánlivou svítivost hvězdy, tak lze určit svítivost absolutní. Porovnáním zdánlivé a absolutní svítivosti lze pak snadno určit vzdálenost soustavy, v níž se cefeidy nacházejí. Tato metoda umožnila měření vzdáleností u soustav, v nichž ještě rozeznáme jednotlivé hvězdy a můžeme tedy měřit změny jejich svítivosti. Vzdálenosti se najednou daly měřit až do několika desítek milionů světelných roků, jelikož se proměřují jen v čase proměnlivé světelné křivky hvězd a porovnávají se s předpovězeným modelem.

Pro metody založené na proměřování intenzity svitu vzdálených dějů se ujalo označení „standardní svíčka“. Principem je dobře popsaná astrofyzikální událost, která má standardní průběh a víme tedy, jak by takový děj měl vypadat v nějaké kalibrované vzdálenosti. Pokud pak takovou událost ve vesmíru pozorujeme, tak je možné jen porovnáním pozorování s předpovězeným modelem určit díky předpokládanému úbytku svítivosti vzdálenost, v jaké se odehrála. Samozřejmě je nutno vzít v úvahu, že úbytek světla nemusí být způsoben jen a pouze zvětšením vzdálenosti, ale může mít i jiné příčiny, například vesmírnou extinkciExtinkce – zeslabení světla vzdálených hvězd. Je způsobena pohlcováním světla mezihvězdnou látkou. V galaktické rovině v bezprostředním okolí Slunce jde o průměrné zeslabení o 1,9 mag/1 kpc. Mezihvězdná látka ale není v Galaxii rozmístěna rovnoměrně a na větších vzdálenostech může nabývat i velmi rozdílných hodnot. Velikost extinkce je zhruba nepřímo úměrná vlnové délce světla. Z velkých vzdáleností tedy lépe prochází mezihvězdným prostředím červené světlo a vzdálenější hvězdy se proto jeví červeně. Extinkce je způsobena rozptylem a pohlcováním fotonů na částicích prostředí. Z charakteristik extinkce lze tak přímo zjistit vlastnosti mezihvězdného prostředí, které nás dělí od zdroje světla.. O to jsou tyto metody záludnější. Důležité ale je, že jsou použitelné na mnohem větší vzdálenosti než metody založené na trigonometrii. Současně je bylo možno v případě cefeid kalibrovat právě trigonometrickými metodami, neb mnoho cefeid se nachází ve vzdálenostech, které se dají ověřit paralaxou.

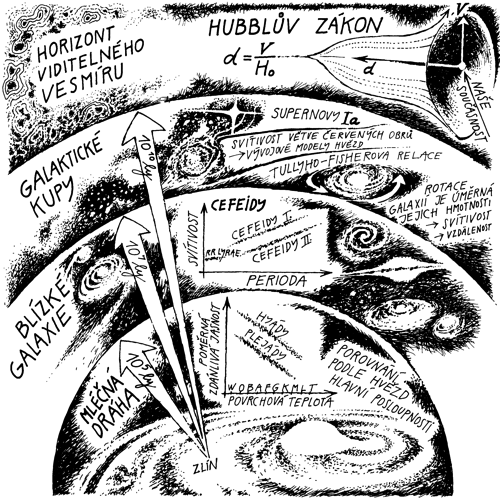
Měření středních a velkých vzdáleností. Kresba Ivan Havlíček.

Tullyho-Fischerova relace

Jsou ale měřitelné vzdálenosti i u objektů, u nichž nerozlišíme jednotlivé hvězdy? Na tuto otázku odpověděli kladně Richard Brent Tully a James Richard Fisher článkem ze 3. února 1977: Nová metoda zjišťování vzdáleností galaxií. Pro tuto metodu se ujal název Tullyho-Fischerova relace a je založena na předpokladu, že rychlost rotace spirálních galaxií (a s ní souvisící rozšíření spektrálních čar) závisí na jejich celkové hmotnosti (a tím svítivosti). Čím je galaxie větší, tím je také hmotnější, rychleji rotuje, a současně také díky většímu počtu hvězd a svítící látky také více svítí. Tullyho-Fischerova relace byla založena na měření potřebných parametrů u Místní skupiny galaxií, Skupiny M 81, Skupiny M 101, kupy galaxií v Panně a galaktické kupy Ursa Major. Mnohá další měření tuto závislost později potvrdila a upřesnila. Dnes lze Tullyho-Fischerovu relaci považovat za hodnověrnou metodu pro zjišťování vzdáleností v případech, kdy jsme spektroskopicky schopni určit parametry rotace galaxie.

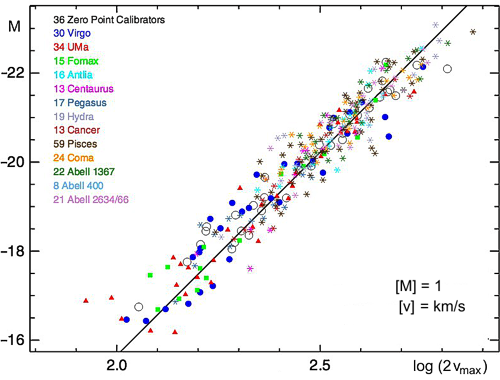
Kalibrace Tullyho-Fischerovy relace pro několik galaktických kup a jejích členů pořízená infračervenou observatoří WISE (viz AB 39/2013) v oboru 3,4 a 4,6 mikronů. Rotace galaxií je v grafu znázorněna na vodorovné ose (vzrůstá směrem doprava), na svislé ose je absolutní magnituda, tedy logaritmus svítivosti souvisící s celkovou hmotností jednotlivých galaxií. Zdroj: Neill et al.

Měření velkých vzdáleností, supernovy Ia

Jsou ale vzdálenosti natolik velké, že ani galaxie jako jednotlivé členy, u nichž bychom dokázali určit něco jako parametry rotace už nejsou rozeznatelné. Z těch nejvzdálenějších končin vesmíru k nám dolétne světlo skutečně jen těch nejsvítivějších zdrojů a jimi jsou extrémně zářivá aktivní galaktická jádra nebo události vydávající v krátkém okamžení svit jako celá galaxie najednou. Takovými událostmi mohou být například supernovy IaSupernova typu Ia – závěrečné vývojové stádium těsné dvojhvězdy. Tvoří-li dvojhvězdu bílý trpaslík a obr (veleobr) nebo hvězda hlavní posloupnosti, může docházet k přenosu látky na bílého trpaslíka, který tak zvětšuje svoji hmotnost. Po překročení Chandrasekharovy meze (1,4 M_S) se bílý trpaslík zhroutí do neutronové hvězdy, dojde k explozivnímu termonukleárnímu hoření C a O na ⁵⁶Ni v celém objemu trpaslíka a uvolněná potenciální energie se projeví jako supernova typu Ia. Množství energie je vždy zhruba stejné, takže z relativní pozorované jasnosti lze vypočítat vzdálenost příslušné supernovy. Přesnější hodnoty se pak určí z tvaru světelné křivky (z průběhu nárůstu a poklesu jasnosti). Supernovu typu Ia lze identifikovat podle tvaru jejího spektra, ve kterém chybí čáry vodíku a jsou přítomné čáry křemíku.. Jde o metodu „standardní svíčky“ avšak v trochu razantnějším provedení. V soustavě těsné dvojhvězdy postupně přetéká látka z obra na bílého trpaslíkaBílý trpaslík – jedna z možných závěrečných fází vývoje hvězd. Hvězda, ve které degenerovaný elektronový plyn vyvíjí gradient tlaku (způsobený Pauliho vylučovacím principem), který odolává gravitaci. Poloměr je 1 000 km až 30 000 km, hustota řádově 10³ kg cm^-3, maximální hmotnost 1,4 M_S. Hmotnější bílí trpaslíci jsou nestabilní, explodují jako supernovy typu Ia. Tuto tzv. Chandrasekharovu mez odvodil Subrahmanyan Chandrasekhar v roce 1930. Objev prvního bílého trpaslíka: Již v roce 1834 Fridrich Bessel předpověděl průvodce Síria A z newtonovské teorie na základě vlnovkovité trajektorie hvězdy Sírius. Tento průvodce (Sírius B) byl objeven v optické dílně bratří Clarků roku 1862 (Alvan Clark – test objektivu průměru 45 cm). Sírius B je prvním známým bílým trpaslíkem. Byla na něm demonstrována správnost newtonovské teorie (vlnovkovitá trajektorie Síria A) i potvrzena OTR (červený posuv). Sírius B je enormně malý a hustý bílý trpaslík s průměrem 11 736 km, ρ = 3×10³ kg cm⁻³. Povrchová teplota je 24 800 K, vzdálenost 8,6 l.y. a hmotnost 1,03 M_S. a při překročení Chandrasekharovy mezeChandrasekharova mez – Mez stability bílého trpaslíka. Nad hodnotou 1,4 M_S je bílý trpaslík nestabilní a rozmetá ho termojaderná exploze. Mez spočítal indický fyzik Subramanyan Chandrasekhar. (1,4 M_S) se bílý trpaslík zhroutí do neutronové hvězdy. Jelikož k tomu dojde při vždy téměř shodných podmínkách, lze tento děj považovat za vždy téměř stejně probíhající včetně množství energie, která se při něm uvolní. Vyzářená energie je srovnatelná se svitem celé galaxie, přičemž podle světelné křivky a spektrální analýzy lze událost určit jako supernovu Ia. Supernovy Ia jsou vyhledávány přehlídkovými projekty již od konce devadesátých let minulého století a za objev zrychlené expanze vesmíru zjištěný právě díky možnosti měření kosmologických vzdáleností pomocí supernov Ia byla v roce 2011 udělena Nobelova cena za fyziku Adamu Guy Riessovi, Brianu Schmidtovi a Saulu Perlmutterovi (viz AB 39/2011).

Expanze vesmíru

Jako poslední metodu určování vzdáleností ve vesmíru je nutno zmínit měření vzdálenosti z rychlosti vesmírné expanze galaxií a jejich soustav. Rozpínání vesmíru bylo teoreticky předpovězeno na počátku dvacátého století Einsteinovou obecnou teorií relativityObecná relativita – teorie gravitace publikovaná Albertem Einsteinem v roce 1915. Její základní myšlenkou je tvrzení, že každé těleso svou přítomností zakřivuje prostor a čas ve svém okolí. Ostatní tělesa se v tomto pokřiveném světě pohybují po nejrovnějších možných drahách, tzv. geodetikách., diskutováno a rozpracováno mnoha Einsteinovými následovníky. Podrobněji je tato oblast zpracována v kapitole věnující se kosmologii. Červený posuvKosmologický posuv – posuv spektrálních čar k červenému konci spektra díky rozpínání vesmíru. Při rozpínání dochází nejen ke vzájemnému vzdalování galaxií, ale i k prodlužování vlnových délek záření. Spektrum vzdálených objektů ve vesmíru se tak jeví posunuté směrem k červené až infračervené oblasti. Kosmologický červený posuv je definován předpisem z = (λ − λ₀)/λ₀, kde λ₀ je vlnová délka spektrální čáry v okamžiku vyslání paprsku, λ je vlnová délka téže spektrální čáry v okamžiku zachycení paprsku. Malé kosmologické červené posuvy lze interpretovat pomocí Dopplerova jevu. U velkých posuvů závisí vzdálenost objektu na parametrech expanze vesmíru (Hubbleově konstantě, křivosti, procentuálním zastoupení temné energie atd.) a není jednoduché z naměřeného kosmologického posuvu vzdálenost přesně určit. Proto se většinou časové období udává pouze hodnotou naměřeného kosmologického posuvu. projevující se při vzdalování galaxií objevil Vesto Slipher již v letech 1912 až 1915 na Lowellově hvězdárně ve Flagstaffu. Tento jev ale interpretoval jako expanzi vesmíru až v roce 1927 belgický kněz Georges Lemaître. O dva roky později expanzi vesmíru s velkou pompou znovuobjevil na observatoři Mount Wilson americký astronom Edwin Hubble. Článek vyšel 17. ledna 1929 pod názvem A relation between distance and radial velocity among extra-galactic nebulae. Na šesti stránkách byly tři tabulky s daty, jeden graf a doprovodný text, v němž Hubble uváděl, že galaxie se od nás vzdalují tím rychleji, čím jsou dál. Stejný jev už ale dva roky předtím popsal mnohem pečlivěji Lemaître.

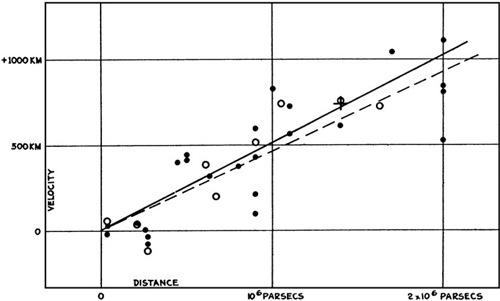
Graf z článku Edwina Hubbla A relation between distance and radial
velocity among extra-galactic nebulae z roku 1929.

Pro koeficient úměrnosti mezi rychlostí vzdalování a vzdáleností se později vžil termín Hubblova konstantaHubblova konstanta – koeficient úměrnosti mezi rychlostí vzdalování a vzdáleností objektů při expanzi vesmíru (H = v/R). Přesnější definice je dána přes expanzní funkci a: H = (da/dt)/a. Dnes se hodnota Hubblovy konstanty odhaduje na přibližně 70 km/s na megaparsek. Různé metody dávají poněkud odlišné výsledky, což je buď způsobeno systematickými chybami v odhadu vzdáleností, nebo nepřesným kosmologickým modelem. a její dnešní hodnota činí 67 km s⁻¹ Mpc⁻¹. Vzdálenosti lze ve vesmíru tedy za určitých předpokladů měřit i v místech, ve kterých si nejsme příliš jisti, na jaké objekty se zrovna díváme. Stačí u nich jen určit z kosmologického posuvuKosmologický posuv – posuv spektrálních čar k červenému konci spektra díky rozpínání vesmíru. Při rozpínání dochází nejen ke vzájemnému vzdalování galaxií, ale i k prodlužování vlnových délek záření. Spektrum vzdálených objektů ve vesmíru se tak jeví posunuté směrem k červené až infračervené oblasti. Kosmologický červený posuv je definován předpisem z = (λ − λ₀)/λ₀, kde λ₀ je vlnová délka spektrální čáry v okamžiku vyslání paprsku, λ je vlnová délka téže spektrální čáry v okamžiku zachycení paprsku. Malé kosmologické červené posuvy lze interpretovat pomocí Dopplerova jevu. U velkých posuvů závisí vzdálenost objektu na parametrech expanze vesmíru (Hubbleově konstantě, křivosti, procentuálním zastoupení temné energie atd.) a není jednoduché z naměřeného kosmologického posuvu vzdálenost přesně určit. Proto se většinou časové období udává pouze hodnotou naměřeného kosmologického posuvu. rychlost vzdalování, a tu pak pomocí Hubblovy konstanty umíme přepočítat na vzdálenost. Jelikož je ale rychlost vzdalování veličina přímo měřitelná a Hubblova konstanta je jen veličina odvozená na základě mnoha nejistých předpokladů, udávají se velmi velké vzdálenosti v kosmologických textech pro jistotu jen v hodnotách změřeného červeného posuvu spektrálních čar. Odpadá tak pro budoucí interpretace nutnost zpětného zjišťování metody, s jakou byl červený posuv na vzdálenost přepočítán a jaké předpoklady byly brány pro výpočet v úvahu.