Kosmologie | Standardní kosmologický model
Olbersův paradox
Počet hvězd v sférické slupce roste s druhou mocninou vzdálenosti slupky. Intenzita záření přicházející k pozorovateli naopak klesá s druhou mocninou vzdálenosti. Oba jevy by se tak měly vyrušit a k pozorovateli by všechny sférické slupky z celého vesmíru (je jich nekonečně mnoho) měly přispět stejnou intenzitou. Výsledkem by měl být nekonečný jas denní i noční oblohy. Provedeme-li opravu na zákryty hvězd, absorpci světla atd., stejně dostaneme alespoň konstantní konečný jas oblohy ve dne i v noci. Přesto je v noci tma. Proč? Tento paradox zformuloval německý astronom a lékař Heinrich Olbers (1758–1840) v roce 1832, jeho závěry však byly chybné. Již dříve o tomto paradoxu hlouběji uvažoval Kepler, a proto se také někdy nazývá Keplerův paradox.
- Ve vesmíru dochází evidentně k vývoji jednotlivých objektů, stáří hvězd není neomezené. Hvězdy tedy nevyzařují po nekonečně dlouhou dobu, jak vyžaduje Olbersův paradox.
- Úvaha platí navíc jen pro vesmír nekonečný v prostoru i čase (= neomezeně trvající). Světlo od jednotlivých slupek k nám „cestuje“ určitou dobu. Jestliže vesmír někdy vznikl, ze vzdálenějších slupek k nám žádné světlo nedolétlo, protože vesmír ještě neexistoval. Počet slupek tedy není nekonečný.
- Vesmír se rozpíná, dochází ke kosmologickému červenému posuvu záření a dalšímu snížení intenzity záření.
Olbersův paradox. Nejjednodušším důkazem vývoje objektů ve vesmíru
a jeho proměnlivosti s časem je fakt, že v noci je tma.
Fridmanovo řešení
V roce 1922 ukázal ruský vědec Alexandr Fridman (německý přepis jména je Friedmann), že Einsteinovy rovnice obecné relativity neposkytují konstantní řešení pro homogenní isotropní vesmír. Vesmír musí být nestacionární, buď se rozpíná, nebo se smršťuje. Je to obdobné jako pohyb kamene hozeného vzhůru. Nikdy nezůstane viset ve vzduchu v konstantní vzdálenosti od Země, buď poletí vzhůru, nebo bude padat dolů. Obdobné řešení také nalezl belgický kněz Georges Lemaître. Ten dokonce předpověděl červený kosmologický posuvKosmologický posuv – posuv spektrálních čar k červenému konci spektra díky rozpínání vesmíru. Při rozpínání dochází nejen ke vzájemnému vzdalování galaxií, ale i k prodlužování vlnových délek záření. Spektrum vzdálených objektů ve vesmíru se tak jeví posunuté směrem k červené až infračervené oblasti. Kosmologický červený posuv je definován předpisem z = (λ − λ0)/λ0, kde λ0 je vlnová délka spektrální čáry v okamžiku vyslání paprsku, λ je vlnová délka téže spektrální čáry v okamžiku zachycení paprsku. Malé kosmologické červené posuvy lze interpretovat pomocí Dopplerova jevu. U velkých posuvů závisí vzdálenost objektu na parametrech expanze vesmíru (Hubbleově konstantě, křivosti, procentuálním zastoupení temné energie atd.) a není jednoduché z naměřeného kosmologického posuvu vzdálenost přesně určit. Proto se většinou časové období udává pouze hodnotou naměřeného kosmologického posuvu. vzdálených galaxií. Existenci červeného posuvu spektra galaxií v důsledku expanze vesmíru také nezávisle předpověděl (z obecné relativity) americký matematik a fyzik Howard Percy Robertson (1903–1961) v roce 1928. V rámci historické pravdy je proto třeba říci, že o expanzi vesmíru a jejích důsledcích uvažovalo před Hubblovým objevem více fyziků a Hubblův zákonHubblův zákon – Edwin Hubble zjistil v roce 1929, že čím je galaxie vzdálenější, tím vyšší rychlostí se od nás vzdaluje. Koeficient úměrnosti se nazývá Hubblova konstanta a označujeme ji H. Tento vztah samozřejmě platí jen pro velmi vzdálené galaxie, pro blízké galaxie je rychlost expanze malá a převládají vzájemné pohyby galaxií. Vzhledem k tomu, že vztah objevil Georges Lemaître už v roce 1927, schválila Mezinárodní astronomická unie v roce 2018 rezoluci, podle které se tento zákon má nazývat Hubblův-Lemaîtrův zákon. zformuloval abbé Lemaître už dva roky před Edwinem Hubblem. Hubble o těchto výpočtech pravděpodobně nevěděl. V roce 1929 Hubble správně interpretoval červené posuvy galaxií, experimentálně prokázal expanzi vesmíru a nezávisle objevil lineární vztah mezi rychlostí expanze a vzdáleností. Detailní analýzu všech možných způsobů expanze vesmíru provedl na základě matematické teorie grup anglický matematik Arthur Geoffrey Walker (1909–2001) až v roce 1936. Fridmanova metrika se proto dnes označuje zkratkou FRWL (Fridman, Robertson, Walker, Lemaître). Charakter expanze nebo kolapsu prostorových souřadnic popisuje tzv. expanzní funkce a(t). Můžeme si ji představit jako poměr vzdálenosti libovolných dvou objektů ve vesmíru dnes a v minulosti. Charakter řešení záleží na průměrné hustotě vesmíru ρ a popisuje ho Einsteinova-Fridmanova rovnice:
| Einsteinova-Fridmanova rovnice | |
|---|---|
| H 2 − (8/3)πGρ = −c2k/a2 | Einsteinova-Fridmanova rovnice pro expanzní funkci |
| H ≡ (da/dt)/a | Hubblova konstanta – podíl rychlosti expanze a vzdálenosti objektů |
| a(t) | expanzní funkce (bezrozměrná) |
| da/dt | změna expanzní funkce s časem (1/s) |
| ρ | průměrná hustota vesmíru (kg/m3) |
| k | skalární křivost vesmíru (1/m2) |
| G | gravitační konstanta (Nm2kg–2) |
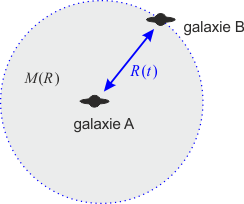
Analogii této rovnice je možné odvodit i v klasické mechanice. Představme si dvě galaxie ve vzdálenosti a. Pohyb galaxie B vzhledem k galaxii A je dán jen hmotou rozprostřenou uvnitř koule se středem v A a poloměrem AB. Předpokládejme, že celková hmotnost v této oblasti je M a průměrná hustota ρ. Napíšeme zákon zachování energie pro galaxii B, dosadíme do něho za hmotnost a nakonec označíme podíl rychlosti da/dt a vzdálenosti a jako H:
Tato rovnice je svým tvarem identická s Einsteinovou-Fridmanovou rovnicí, jen interpretace jednotlivých proměnných se významně liší (vzdálenost ↔ expanzní funkce, celková energie ↔ mínus křivost). Einsteinova-Fridmanova rovnice je diferenciální rovnicí, která spolu s další rovnicí pro hustotu umožňuje nalézt závislost expanzní funkce na čase. V řešení Einsteinovy-Fridmanovy rovnice mohou nastat tři odlišné případy:
- Členy na levé straně rovnice jsou si přesně rovny, vesmír má kritickou hustotu ρc = 3H2/8πG. Křivost na pravé straně je nulová, vesmír je plochý a bude se rozpínat stále. Objem vesmíru je nekonečný.
- Potenciální (druhý) člen převládá nad kinetickým (prvním) členem. Hustota je vyšší než kritická, vesmír má kladnou křivost (ve dvourozměrné analogii by tomu odpovídal tvar povrchu míče). Rozpínání se po nějaké době zastaví a vesmír se začne smršťovat. Objem vesmíru je konečný.
- Kinetický (první) člen převládá nad potenciálním (druhým). Hustota je nižší než kritická, vesmír má zápornou křivost (ve dvourozměrné analogii by tomu odpovídal tvar koňského sedla). Vesmír se bude rozpínat stále. Objem vesmíru je nekonečný, je-li topologie vesmíru jednoduše souvislá (každou křivku lze stáhnout do bodu). Připustíme-li i topologie, které nejsou jednoduše souvislé, může být objem vesmíru konečný i v tomto případě.
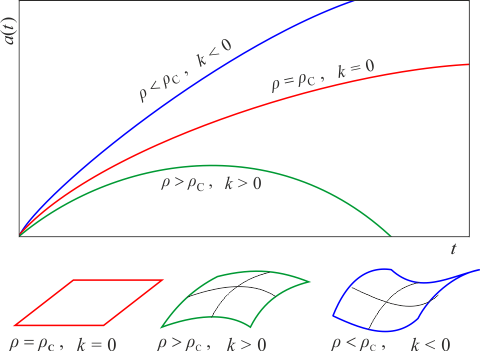
Obecná expanze
Hmotnost a energie jsou provázány Einsteinovým vztahem E = mc2 a mezi hustotami obou veličin platí vztah ρE = ρmc2. V tzv. přirozené soustavě jednotek (c = 1) obě veličiny splývají. V dosavadních vztazích znamenal symbol ρ hustotu hmoty, která má jednotku kg/m3. V následujícím textu budeme symbolem ρ označovat hustotu energie, která má jednotku J/m3. Čtenář by měl při čtení astronomických textů vždy zvážit, o kterou z obou hustot jde. Vesmír se skládá z entit, které se při expanzi chovají různě. Hustota běžné látky (složené z částic s nenulovou klidovou hmotností) klesá při expanzi se třetí mocninou narůstajících rozměrů. Hustota energie záření (reprezentují ho polní částice s nulovou klidovou hmotností) klesá se čtvrtou mocninou, tedy rychleji. Hustota tzv. temné energie s největší pravděpodobností při expanzi neklesá vůbec. Obecně můžeme pokles hustoty dané entity vyjádřit vztahem ρ ~ 1/aα. Z jednoduchých termodynamických úvah (viz sylabus Astrofyzika v příkladech) lze ukázat, že entita klesající při expanzi s mocninnou závislostí na vzdálenostech splňuje jednoduchý vztah
p = wρ
mezi hustotou energie a tlakem (tzv. stavovou rovnici). Koeficient w je podíl tlaku a hustoty energie a patří k velmi důležitým kosmologickým parametrům, jeho hodnota je α/3 − 1. Pro hmotu (α = 3) je parametr w nulový a tato entita nepřispívá při expanzi žádným tlakem. Pro záření (α = 4) je w = +1/3. Jde o známý vztah mezi tlakem záření a hustotou jeho energie p = ρ/3. Pro temnou energii (α < 3) je koeficient w, a tedy i tlak, záporný. Záporný tlak podporuje expanzi vesmíru. Plyne to z rovnice pro zrychlení expanzní funkce:
d2a/dt2/a = −4πG(ρ + 3p)/3
Hodnota koeficientu w pro temnou energii je velmi důležitá. Aby docházelo k pozorované zrychlené expanzi vesmíru, musí podle poslední rovnice platit, že w < −1/3. Pro vakuovou energii spojenou s kvantově mechanickými procesy ve vakuu je w = −1 a expanzní funkce roste exponenciálně. Pro w ∈ (−1,−1/3) hovoříme o tzv. kvintesenciKvintesence – hypotetické kvantové pole, které by mohlo být nositelem páté interakce, která se chová jako dynamická, časově se vyvíjející a prostorově nehomogenní forma energie vykazující tlak dostatečně záporný na to, aby urychlovala rozpínání vesmíru.. Pokud by dokonce bylo w < −1 bude expanze natolik překotná, že zasáhne strukturu látky a rozerve v budoucnu samotná atomová jádra. Hovoříme o tzv. poli fantómů a této situaci říkáme big rip – velké rozervání. Z měření WMAPWMAP – Wilkinson Microwave Anisotropy Probe, sonda z roku 2001, která pořídila podrobnou mapu fluktuací reliktního záření s úhlovým rozlišením kolem 15′ a citlivostí 20 μK. Zrcadlo sondy mělo rozměry 1,4×1,6 m a teplota chlazené části byla nižší než 95 K. Data sondy jsou důležitým zdrojem informací o raných fázích vývoje vesmíru, většinou se kombinují s daty z pozemských zařízení jako je CBI a ACBAR a s daty z novější sondy Planck. Sonda byla umístěna v Lagrangeově bodě L2 soustavy Země-Slunce, kde pracovala do 28. října 2010., PlanckPlanck – mikrovlnná observatoř evropské kosmické agentury ESA, která byla vynesena do vesmíru 14. května 2009. Byla určena k výzkumu fluktuací reliktního záření a monitorování vesmíru v mikrovlnné oblasti. Měla úhlovou rozlišovací schopnost 5′ a teplotní citlivost 2 μK. Oblohu snímkovala v devíti frekvenčních pásmech od 30 do 857 GHz (0,2 až 10 mm). Zrcadlo sondy mělo rozměry 1,9×1,5 m. Teplotu vysokofrekvenční části ohniska se podařilo po dobu dvou let udržet na extrémně nízké hodnotě 0,1 K. Činnost sondy byla ukončena v říjnu 2013., CBICBI – Cosmic Background Imager. Přístroj určený zejména k pozorování reliktního záření. Je umístěn v Atacamské poušti na planině Llano de Chajnantor ve výšce 5 080 metrů. Jde o soustavu třinácti radioteleskopů o průměru 90 cm na společné montáži. CBI je společným projektem univerzit California Institute of Technology, Canadian Institute for Theoretical Astrophysics, University of Chicago, Universidad de Chile a observatoře National Radio Astronomy Observatory., 2dF2dFGRS (2dF Galaxy Redshift Survey) – projekt, v rámci kterého již byla pořízena spektra více jak 260 000 galaxií pomocí zařízení 2dF (2 degree Field) – unikátního spektrografu připojeného k dalekohledu AAT (Anglo Australian Telescope), který má zrcadlo o průměru 3,9 metru a je umístěn od roku 1974 na observatoři AAO (Anglo Australian Observatory) v Austrálii v nadmořské výšce 1 150 m. Spektrograf pořídí v poli o velikosti 2° naráz spektra 400 objektů. a SDSSSDSS – Sloan Digital Sky Survey, ambiciózní projekt přehlídky oblohy podporovaný nadací Alfreda Pritcharda Sloana, která byla založena v roce 1934. Alfred P. Sloan (1875-1976) byl americký obchodník a výkonný ředitel společnosti General Motors po více než dvacet let. Sloanova nadace podporuje také vědu a školství. Projekt katalogizuje všechny galaxie s mezní jasností do 23. magnitudy na čtvrtině severní oblohy. Přehlídka zahrnuje asi 500 miliónů galaxií a ještě více hvězd. U každé galaxie je určena pozice, jasnost a barva. Pro asi milión galaxií a 100 000 kvazarů budou pořízena spektra. Stanice SDSS je postavena v Novém Mexiku v Sacramento Mountains na observatoři Apache Point. Hlavním přístrojem projektu SDSS je dalekohled o průměru primárního zrcadla 2,5 m. vychází, že parametr w se pro temnou energii nachází v intervalu hodnot <−1;−0,78) a scénář velkého rozervání je s nejvyšší pravděpodobností experimentálně vyloučen. V mnoha kosmologických modelech se uvažuje u parametru w o lineární závislosti na samotné hodnotě expanzní funkce:
w = w0 + wa(1 − a)
Pro vakuovou energii by mělo být w0 = −1, wa = 0. Pro dominující druhý člen, kdy se w s expanzí výrazně mění a přechází přes hodnotu w = −1 hovoříme o poli kvintonů. Dalším velmi důležitým pojmem je horizont částic RH. Jde o maximální vzdálenost, ze které k nám dolétly částice za dobu existence vesmíru. Této vzdálenosti se také někdy říká horizont pozorovatelného vesmíru, protože do větší vzdálenosti není možné dohlédnout, i když tam také částice jsou. Ani nejrychlejší částice, fotony, k nám ze vzdálenějších oblastí nestihly dolétnout. V sylabu Astrofyzika v příkladech je vypočten horizont částic pro různé expanzní funkce. Látce, záření a vakuové hustotě energie odpovídají různá řešení Einsteinovy rovnice pro expanzní funkci:
| α | a(t) | H(t) | p(ρ) | w | RH | |
| obecná entita | α | ~ t2/α | 2/αt | p = wρ | α/3 − 1 | α/(α–2) ct |
| záření | 4 | ~ t1/2 | 1/2t | p = ρ/3 | 1/3 | 2ct |
| látka | 3 | ~ t2/3 | 1/3t | p = 0 | 0 | 3ct |
| křivost (k<0) | 2 | ~ t | 1/t | p = –ρ/3 | –1/3 | – |
| energie vakua | 0 | ~ eχt | χ | p = −ρ | −1 | – |
Ve sloupcích tabulky jsou postupně mocnina α, se kterou ubývá hustota energie se vzdáleností, expanzní funkce a, Hubblova konstanta H, parametr stavové rovnice w a horizont částic RH. Detaily jsou v sylabu Astrofyzika v příkladech.
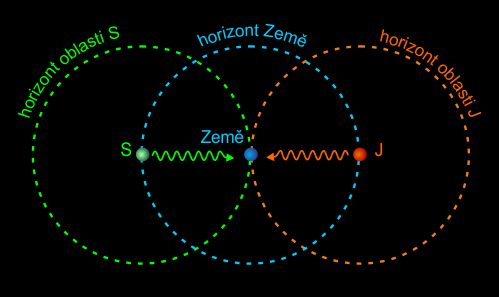
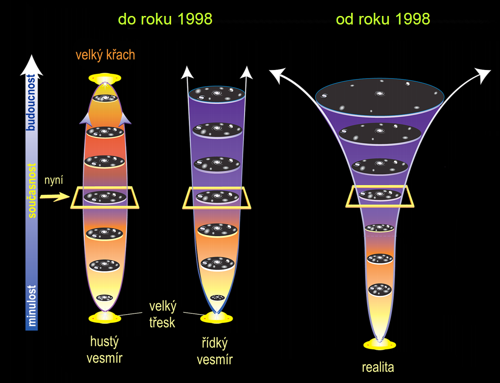
Při pohledu na sever i na jih vidíme v nejvzdálenější oblasti reliktní záření z konce Velkého třesku. To je horizont našeho pohledu, který je na obrázku vyznačen modrou přerušovanou linií. Dále sice vesmír pokračuje, ale my tyto oblasti nespatříme, protože by světlo z nich k nám letělo déle, než vesmír existuje. Světelný signál se šíří se zpožděním, takže tam, kde my vidíme konec Velkého třesku, jsou dnes hvězdy a galaxie, stejně jako v našem okolí. Naopak „seveřan“ a „jižan“ z míst S a J uvidí konec Velkého třesku u nás. Každý pozorovatel má svůj horizont, v němž je uzavřen pro něho pozorovatelný vesmír.
Kosmologická konstanta
Einsteinovy rovnice obecné relativity mají jednoduchý tvar
Gμν = κTμν.
Člen nalevo (Einsteinův tenzor) popisuje zakřivení časoprostoru a skládá se z různých kombinací metriky gμν a jejích derivací. Napravo je tzv. tenzor energie a hybnosti, který popisuje rozložení látky ve vesmíru. Einsteinovy rovnice obecné relativity jsou pouze matematickým vyjádřením skutečnosti, že látka kolem sebe zakřivuje prostor a čas. Koeficient úměrnosti mezi Einsteinovým tenzorem G a tenzorem T vychází (z požadavku, aby v případě slabých polí daly Einsteinovy rovnice Newtonův gravitační zákon) κ = 8πG/c4. V roce 1917 dodal Einstein na levou stranu navíc člen úměrný metrickému tenzoru, který měl zajistit stacionární řešení Einsteinových rovnic, neboť Einstein, podobně jako jeho současníci, věřil, že vesmír je neměnný v čase. Vlastní gravitací by ale takový vesmír kolaboval, proto do rovnic dodal člen s opačným účinkem, než má gravitace:
Gμν + Λgμν = κTμν.
Koeficient úměrnosti Λ se nazývá kosmologická konstanta (v soustavě jednotek SI má rozměr má 1/m2) a pro některé její hodnoty poskytují „nové“ rovnice obecné relativity i stacionární řešení. Řešením Einsteinových rovnic s nenulovou kosmologickou konstantou se zabýval například belgický kněz Georges Lemaître (1894–1966). Po Hubblově objevu rozpínání vesmíru Albert Einstein tento člen z rovnic opět vyškrtl a prohlásil, že šlo o největší omyl jeho života. Dnešní doba znamená velkou renesanci kosmologické konstanty. Člen úměrný metrickému tenzoru do rovnic skutečně patří, je však pravděpodobně způsoben kvantově polními projevy vakua a jeho původ je v kvantových procesech. Pro kvantové vakuum není střední hodnota tenzoru energie a hybnosti na pravé straně Einsteinových rovnic nulová, ale je úměrná metrickému tenzoru:
<Tμν> = ρvakua gμν.
Střední hodnota vakuové energie se proto chová stejně jako člen s kosmologickou konstantou na levé straně rovnic. Kvantové procesy tak do rovnic přirozeným způsobem zavádějí člen úměrný metrickému tenzoru. Otevřenou otázkou zůstává, zda jsou kvantové procesy jediným zdrojem kosmologického členu. Na velkých měřítcích se člen pro některé hodnoty Λ projevuje jako jakási „odpudivá“ gravitace, nebo chcete-li záporný tlak či antigravitace. Projevy tohoto členu jsou dnes pozorovány jako zrychlená expanze vesmíru. K hustotě vesmíru způsobující jeho zakřivení přispívá záření (R), látka (M) a kvantové efekty (Λ)
Ω ≡ ρ/ρc = ΩR + ΩM + ΩΛ.
Pro plochý vesmír by bylo Ω = 1. Dnešní vesmír se zdá být přibližně plochý (Ω = 1,02 ± 0,02) a kosmologická konstanta přispívá hodnotou (Adam Riess – 1998, Saul Perlmutter – 1999).
ΩΛ = c2Λ / 3H 2 ~ 0,68.
Měření byla prováděna na souboru supernov typu IaSupernova typu Ia – závěrečné vývojové stádium těsné dvojhvězdy. Tvoří-li dvojhvězdu bílý trpaslík a obr (veleobr) nebo hvězda hlavní posloupnosti, může docházet k přenosu látky na bílého trpaslíka, který tak zvětšuje svoji hmotnost. Po překročení Chandrasekharovy meze (1,4 MS) se bílý trpaslík zhroutí do neutronové hvězdy, dojde k explozivnímu termonukleárnímu hoření C a O na 56Ni v celém objemu trpaslíka a uvolněná potenciální energie se projeví jako supernova typu Ia. Množství energie je vždy zhruba stejné, takže z relativní pozorované jasnosti lze vypočítat vzdálenost příslušné supernovy. Přesnější hodnoty se pak určí z tvaru světelné křivky (z průběhu nárůstu a poklesu jasnosti). Supernovu typu Ia lze identifikovat podle tvaru jejího spektra, ve kterém chybí čáry vodíku a jsou přítomné čáry křemíku., ve kterých je exploze způsobena rozmetáním bílého trpaslíka, který překročil Chandrasekharovu mezChandrasekharova mez – Mez stability bílého trpaslíka. Nad hodnotou 1,4 MS je bílý trpaslík nestabilní a rozmetá ho termojaderná exploze. Mez spočítal indický fyzik Subramanyan Chandrasekhar.. Shodná hmotnost meze pro tyto trpaslíky vede ke stejné absolutní magnituděMagnituda absolutní – absolutní hvězdná velikost je magnituda objektu, kterou by měl ve vzdálenosti 10 pc od nás. Závisí jen na skutečné svítivosti objektu. Zadáváme-li vzdálenost objektu v parsecích, platí mezi absolutní (M) a relativní magnitudou (m) jednoduchý vztah: M = m + 5 – 5 log r. Rozlišujeme bolometrickou absolutní magnitudu (v celém spektru) a vizuální absolutní magnitudu (pouze v rámci viditelného spektra). Pro určování vzdáleností se někdy využívají proměnné cefeidy, jejichž absolutní magnituda (svítivost) souvisí s periodou světelné křivky P vyjádřenou ve dnech podle přibližného vztahu M = –2.4 log P – 1.5. Ze známé periody a relativní magnitudy určíme z posledních dvou vztahů snadno vzdálenost cefeidy. supernov typu Ia. Vzdálenější supernovy byly méně jasné než podle propočtů. Z toho lze usuzovat na zrychlování expanze vesmíru způsobené nenulovou kosmologickou konstantou. Zrychlování expanze může v budoucnu přerůst v exponenciální fázi expanze vesmíru. Nezávislé měření hodnoty kosmologické konstanty bylo provedeno z rozboru fluktuací reliktního záření měřených sondami WMAPWMAP – Wilkinson Microwave Anisotropy Probe, sonda z roku 2001, která pořídila podrobnou mapu fluktuací reliktního záření s úhlovým rozlišením kolem 15′ a citlivostí 20 μK. Zrcadlo sondy mělo rozměry 1,4×1,6 m a teplota chlazené části byla nižší než 95 K. Data sondy jsou důležitým zdrojem informací o raných fázích vývoje vesmíru, většinou se kombinují s daty z pozemských zařízení jako je CBI a ACBAR a s daty z novější sondy Planck. Sonda byla umístěna v Lagrangeově bodě L2 soustavy Země-Slunce, kde pracovala do 28. října 2010. (2003) a PlanckPlanck – mikrovlnná observatoř evropské kosmické agentury ESA, která byla vynesena do vesmíru 14. května 2009. Byla určena k výzkumu fluktuací reliktního záření a monitorování vesmíru v mikrovlnné oblasti. Měla úhlovou rozlišovací schopnost 5′ a teplotní citlivost 2 μK. Oblohu snímkovala v devíti frekvenčních pásmech od 30 do 857 GHz (0,2 až 10 mm). Zrcadlo sondy mělo rozměry 1,9×1,5 m. Teplotu vysokofrekvenční části ohniska se podařilo po dobu dvou let udržet na extrémně nízké hodnotě 0,1 K. Činnost sondy byla ukončena v říjnu 2013. (2013). Podrobněji se s oběma experimenty seznámíme v kapitole Současná kosmologie. Einsteinova-Fridmanova rovnice pro expanzní funkci má v přítomnosti kosmologické konstanty tvar (hustota je opět v kg/m3)
H 2 − (8/3)πρG − Λ/3 = −c2k/a2.
Pokud členy přeskupíme a nalevo ponecháme jen časový vývoj, dostaneme rovnici
H 2 = (8/3)πρRG + (8/3)πρMG − c2k/a2 + Λ/3.
Probíhající expanzi nejprve ovlivňuje záření (~1/a4), poté látka (~1/a3), pokud je křivost nenulová, následuje éra vlivu zakřivení vesmíru (~1/a2) a nakonec éra zrychlené expanze (~1/a0) daná kosmologickým členem (tzv. de Sitterův vesmír). Na levé straně rovnosti je druhá mocnina Hubblovy konstanty. Pokud celou rovnici vydělíme levou stranou, získáme rovnost:
1 = ΩR + ΩM − Ωk + ΩΛ.
Pro plochý vesmír je Ωk nulové a vztah přejde ve výše uvedenou relaci pro plochý vesmír. Podle současných měření expanze vesmíru, zejména z projektu SPC (Supernova Cosmology Project), vychází hodnota kosmologické konstanty přibližně Λ = 2×10−52 m−2.
Červený posuv galaxií
Edwin Hubble pozoroval galaxie na observatoři Mt. Wilson zrcadlovým dalekohledem o průměru 250 cm. V té době šlo o největší dalekohled na světě. Hubble dokázal, že některé spirální a eliptické mlhoviny jsou ve skutečnosti galaxie složené z hvězd. Navrhl první metody odhadu vzdálenosti galaxií podle nejjasnějších hvězd. V roce 1929 experimentálně zjistil červený posuv vzdálených galaxií. Všechny spektrální čáry jsou u vzdálených galaxií posunuty k červenému konci spektra. To podle Dopplerova jevuDopplerův jev – změna frekvence vlnění při vzájemném pohybu zdroje a pozorovatele. Přibližuje-li se pozorovatel ke zdroji, naměří vyšší frekvenci, než když se vzdaluje. Může jít o zvukové, elektromagnetické i jakékoli jiné vlnění. Jev poprvé popsal rakouský matematik a fyzik Christiaan Doppler (1803–1853), který část svého krátkého života strávil jako profesor pražské Polytechniky, předchůdkyni dnešního ČVUT v Praze. znamená, že se všechny vzdálené galaxie od nás vzdalují. Interpretace přes Dopplerův jev je vhodná jen jako první přiblížení skutečnosti. Pro správnou interpretaci měření je třeba data interpretovat jako kosmologický červený posuvKosmologický posuv – posuv spektrálních čar k červenému konci spektra díky rozpínání vesmíru. Při rozpínání dochází nejen ke vzájemnému vzdalování galaxií, ale i k prodlužování vlnových délek záření. Spektrum vzdálených objektů ve vesmíru se tak jeví posunuté směrem k červené až infračervené oblasti. Kosmologický červený posuv je definován předpisem z = (λ − λ0)/λ0, kde λ0 je vlnová délka spektrální čáry v okamžiku vyslání paprsku, λ je vlnová délka téže spektrální čáry v okamžiku zachycení paprsku. Malé kosmologické červené posuvy lze interpretovat pomocí Dopplerova jevu. U velkých posuvů závisí vzdálenost objektu na parametrech expanze vesmíru (Hubbleově konstantě, křivosti, procentuálním zastoupení temné energie atd.) a není jednoduché z naměřeného kosmologického posuvu vzdálenost přesně určit. Proto se většinou časové období udává pouze hodnotou naměřeného kosmologického posuvu.. Obdobná měření konal již dříve Vesto Slipher, ale nedokázal je správně interpretovat. Edwin Hubble zjistil, že čím jsou galaxie vzdálenější, tím větší červený posuv ve spektru mají, tj. tím rychleji se vzdalují. To vystihuje Hubblův vztah v = H d. Dnešní hodnota Hubblovy konstanty a veličin z ní odvozených (viz dále) je:
| Hubblova konstanta | H | 68 km s−1 Mpc−1 |
| Hubblův čas | 1/H | 14,6 miliard let |
| Hubblova vzdálenost | c/H | 4 500 Mpc |
| kritická hustota | ρc = 3H2/(8πG) |
0,84×10−26 kg/m3 (5 nukleonů na 1 m3) |
Hubblův čas je maximální doba stáří vesmíru, Hubblova vzdálenost
je velikost pozorovatelného vesmíru a kritická hustota je hustota
hmoty ve vesmíru nutná k jeho uzavření. V průběhu experimentů se hodnota Hubblovy konstanty výrazně měnila podle zpřesňování metod odhadu vzdálenosti
galaxií. Poslední a nejpřesnější hodnota je z pozorování sondy PlanckPlanck – mikrovlnná observatoř evropské kosmické agentury ESA, která byla vynesena do vesmíru 14. května 2009. Byla určena k výzkumu fluktuací reliktního záření a monitorování vesmíru v mikrovlnné oblasti. Měla úhlovou rozlišovací schopnost 5′ a teplotní citlivost 2 μK. Oblohu snímkovala v devíti frekvenčních pásmech od 30 do 857 GHz (0,2 až 10 mm). Zrcadlo sondy mělo rozměry 1,9×1,5 m. Teplotu vysokofrekvenční části ohniska se podařilo po dobu dvou let udržet na extrémně nízké hodnotě 0,1 K. Činnost sondy byla ukončena v říjnu 2013.. Rozpínání vesmíru s rychlostí úměrnou vzdálenosti je geometricky
možné jen ve vesmíru, který se současně rozpíná z každého bodu. Ve dvourozměrné
analogii si můžeme představit povrch nafukujícího se balónku, na kterém
jsou namalovány tečky, představující galaxie. Každý bod se zdá být středem
rozpínání, a čím vzdálenější bod od něho pozorujeme, tím rychleji se vzdaluje. Střed balónku
nemá žádný hlubší význam, protože je mimo povrch balónku tvořícího „vesmír“.
Povšimněte si, že vesmír jako celek se rozpíná. Rozměry jednotlivých galaxií
se však nemění. Jsou dány hodnotou gravitační konstanty, která se v průběhu
rozpínání nemění. Stejně tak se nemění expanzí vesmíru rozměry člověka.
Ty jsou dány elektromagnetickou interakcí, tj. hodnotou elektromagnetického
náboje a permitivitou či permeabilitou vakua (resp. hodnotou rychlosti
světla ve vakuu). Představte si prádelní gumu s navěšenými sponkami (viz
kapitola Principy). Pokud
gumu natahujeme, je každé místo středem expanze. Expanduje guma, nikoli sponky.

Hubblovo pozorování je jedním z nejdůležitějších experimentálních důkazů rozpínání vesmíru. Hubblova konstanta souvisí s kritickou hustotou (dosadíme Hubblův vztah H = v/d = (da/dt)/a do vztahu pro kritickou hustotu) rovnicí
ρc = 3H2/(8πG).
S kritickou hustotou souvisí další dva významné kosmologické parametry:
Ω ≡ ρ/ρc,
ε ≡ Ω − 1 .
(Ω = 1, ε = 0 pro plochý vesmír).
Kdybychom extrapolovali dnešní rozpínání do minulosti, určili bychom stáří
vesmíru jako dobu 1/H. Rozpínání vesmíru se však v první polovině
jeho existence zpomalovalo, v druhé polovině naopak dochází ke zrychlené
expanzi.Proto je skutečné stáří vesmíru jiné
než hodnota 1/H. Dnes se z rozboru fluktuací reliktního
záření odhaduje stáří vesmíru na 13,8 miliard let.
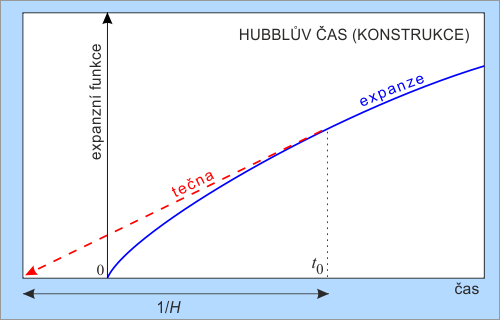
Edwin Hubble měřil tzv. červený posuv z = Δλ/λ. Červené posuvy naměřené Hubblem byly menší než 0,003. Pro takto blízké galaxie lze červený posuv galaxií interpretovat jako Dopplerův jev z ~ v/c. Pro vzdálenější objekty a vyšší hodnoty z je změna frekvence způsobena rozpínáním geometrie vesmíru (kosmologický červený posuv) a hodnotu z je třeba interpretovat jako [a(t)−a(t0)]/a(t0). Například velmi vzdálenou pozorovanou galaxií je objekt UDFy-38135539 s červeným posuvem z = 8,6. Světlo opustilo tento objekt pouhých 600 milionů let po Velkém třesku.
Scénář horkého původu vesmíru
George Gamow vytvořil spolu se svými studenty Ralphem Alpherem a Robertem Hermanem první scénář horkého vzniku vesmíru. Vytvořili model vzniku lehkých prvků v prvopočátečním plazmatu. Současně přišli na to, že by se v chladnoucím vesmíru mělo v určitém období oddělit záření od látky. V roce 1948 publikovali dva články, z nichž na jednom se podepsal na naléhání Gamowa i jaderný fyzik Hans Bethe. Tím se autory stali Alpher, Bethe a Gamow, což připomínalo řecká písmena alfa, beta a gama a naznačilo principiální důležitost modelu...
Gamow počítal se svými studenty, jak se v průběhu Velkého třesku tvořily prvky. Za teplot miliard stupňů došlo k vytvoření vodíku, helia a dalších lehkých prvků. Určili procentuální zastoupení jednotlivých lehkých prvků ve vesmíru (podle tehdejších modelů silné interakce), které ne zcela odpovídalo skutečnosti, ale podle dnešních modelů silné interakce je jejich model v dobré shodě se skutečností. (Těžké prvky vznikaly až v nitru hvězd). Byl-li vesmír ve svých raných fázích horký, záření bylo vázáno na látku. Tím se rozumí, že kvanta záření – fotony – intenzivně interagovala s volnými elektrony, které byly v počátečním plazmatuPlazma – kvazineutrální soubor nabitých a neutrálních částic, který vykazuje kolektivní chování. Lidsky to znamená, že se v dané látce nachází elektricky nabité částice. Kladné a záporné náboje se navzájem kompenzují, takže celek je elektricky neutrální. Částice jsou schopné reagovat na elektrická a magnetická pole jako celek. Plazma vzniká odtržením elektronů z elektrického obalu atomárního plynu nebo ionizací molekul. S plazmatem se můžeme setkat v elektrických výbojích (blesky, jiskry, zářivky), v polárních zářích, ve hvězdách, ve slunečním větru a v mlhovinách. Pro plazma jsou typické silně nelineární jevy a nestability. Přes 99 % atomární látky ve vesmíru je v plazmatickém skupenství. hojně zastoupeny. Spolu s rozpínáním vesmíru docházelo k chladnutí hmoty se zářením. Asi 380 000 let po vzniku vesmíru končí jeho plazmatická éra, a tím i Velký třesk. Volné elektrony se stávají součástí atomárních obalů a látka je od této chvíle elektricky neutrální. Právě volné elektrony doposud udržovaly kontakt záření s látkou. Vesmír se stal pro záření průhledným a interakce záření s hmotou minimální. Záření se oddělilo od látky a započalo svou samostatnou pouť vesmírem. V době oddělené mělo toto záření charakter záření černého tělesaČerné těleso – idealizované těleso, které absorbuje veškeré záření na něho dopadající. Těleso je v termodynamické rovnováze, takže je nakonec veškerá absorbovaná energie opět vyzářena, ale pouze povrchem. Střední volná dráha fotonů je natolik malá ve srovnání s rozměry tělesa, že foton z vnitřku tělesa nemůže uniknout. Na vyzařování se podílejí jen fotony v těsném okolí povrchu. Černé těleso vyzařuje spojité spektrum záření (záření černého tělesa). Maximum vyzařování je na vlnové délce, která souvisí s teplotou povrchu. Čím vyšší je teplota, tím těleso vyzařuje na kratších vlnových délkách..
Přibližně v téže době také poprvé poklesla hustota energie záření (ρ ~ 1/a4) pod hodnotu hustoty energie hmoty (ρ ~ 1/a3). Proto období před oddělením záření od hmoty nazýváme éra záření, následné období éra látky. Podle Stefanova-Boltzmannova zákonaStefanův-Boltzmannův zákon – popisuje celkovou intenzitu vyzařovanou absolutně černým tělesem. Zákon odvodili rakouští fyzikové Josef Stefan a Ludwig Boltzmann. Dnes lze zákon snadno odvodit integrací Planckova vyzařovacího zákona přes všechny frekvence a celý prostorový úhel. Ukazuje se, že celková intenzita vyzařování prudce roste s teplotou, je úměrná její čtvrté mocnině. je celková energie záření úměrná čtvrté mocnině teploty. Z toho je zřejmé, že teplota záření musí klesat jako 1/a. Gamow teoreticky předpověděl, že záření z období oddělení záření od hmoty by dnes mělo být pozorovatelné jako všudypřítomné záření absolutně černého tělesa o teplotě cca 6 K. Toto záření nazýváme reliktní zářeníReliktní záření – záření, které se od látky oddělilo přibližně 400 000 let po vzniku vesmíru, v době, kdy se vytvářely atomární obaly prvků a končilo plazmatické období vesmíru. Počáteční horkou (plazmatickou) fázi existence vesmíru nazýváme Velký třesk a reliktní záření tedy pochází z období konce Velkého třesku. Dnes má teplotu 2,73 K a vlnovou délku v milimetrové oblasti. Je jedním ze základních zdrojů informací pro naše poznání raného vesmíru. V anglické literatuře se označuje zkratkou CMB (Cosmic Microwave Background, mikrovlnné záření pozadí)., jeho skutečná teplota je 2,73 K.
Současné procentuální zastoupení lehkých prvků a později objevené reliktní záření o teplotě 2,73 K lze řadit k dalším experimentálním důkazům existence Velkého třesku.

Tvůrci modelu horkého původu vesmíru: Alfvér, Bethe, Gamow a Herman.
Bethe se mezi ně přidal na přímou žádost Gamowa.
Reliktní záření
Penzias a Wilson (1965)
Reliktní záření objevili na vlnové délce 73,5 mm Arno Penzias a Robert Wilson z Bellových telefonních laboratoří (Murray Hill, New Jersey). Se speciální radiovou anténou z roku 1960 (konstrukci navrhl Arthur Crawford) byly zpočátku sledovány odrazy signálu od družice Echo. Anténa měla nálevkovitý tvar se sběrnou plochou 25 m2. Poměr citlivosti v dopředném a zpětném směru byl 3000:1. V roce 1963 byly ukončeny práce s družicí Echo. Arno Penzias a Robert Wilson chtěli pokračovat s radiovým mapováním Mléčné dráhy a sledováním radiových signálů galaxií, ale úroveň šumu byla obrovská a tisícinásobně převyšovala signál. Při měření mikrovlnného pozadí vyloučili vlastní šum antény, vlnovodu, maseru, konvertoru, oblohy, atmosféry a známých zdrojů. Přesto zůstalo ještě všesměrové záření pozadí, které se chovalo (jak bylo později upřesněno) jako záření absolutně černého tělesa o teplotě 2,7 K (tomu odpovídá vlnová délka maxima vyzařování 1 milimetr). Toto záření nevymizelo ani po dvojím rozebrání a vyčištění antény. Šlo právě o reliktní záření, jehož teplota řádově souhlasí s prvním Gamowovým odhadem. Za tento objev získali Arno Penzias a Robert Wilson v roce 1978 Nobelovu cenuNobelova cena – je udílena švédskou Královskou akademií věd jednou ročně v pěti kategoriích: za fyziku, chemii, fyziologii a medicínu, literaturu a za úsilí o mír. Cena je hrazena z Nobelovy nadace, kterou založil Alfréd Nobel, vynálezce dynamitu, v roce 1895. První cena za fyziku byla udělena v roce 1901 Wilhelmu Roentgenovi za objev rentgenového záření. Hodnota Nobelovy ceny se mění, v roce 2021 činí 10 milionů švédských korun, tj. 25 milionů českých korun. Uděluje se vždy 10. prosince při výročí smrti Alfreda Nobela. za fyziku.
COBE (1989)
Penzias a Wilson měřili na jediné vlnové délce. Mnohem podrobnější měření byla provedena koncem 90. let po vypuštění družice COBECOBE – Cosmic Background Explorer, družice NASA vypuštěná v roce 1989. Pomocí družice bylo zjištěno, že reliktní záření má teplotu 2,73 K a že jde s vysokou přesností o záření absolutně černého tělesa. V roce 1992 družice objevila fluktuace reliktního záření a jeho anizotropii způsobenou naším vlastním pohybem. Rozlišovací schopnost COBE byla 7°. Činnost sondy byla ukončena v roce 1993. v roce 1989. Družice provedla detailní průzkum reliktního zářeníReliktní záření – záření, které se od látky oddělilo přibližně 400 000 let po vzniku vesmíru, v době, kdy se vytvářely atomární obaly prvků a končilo plazmatické období vesmíru. Počáteční horkou (plazmatickou) fázi existence vesmíru nazýváme Velký třesk a reliktní záření tedy pochází z období konce Velkého třesku. Dnes má teplotu 2,73 K a vlnovou délku v milimetrové oblasti. Je jedním ze základních zdrojů informací pro naše poznání raného vesmíru. V anglické literatuře se označuje zkratkou CMB (Cosmic Microwave Background, mikrovlnné záření pozadí).. V průběhu prvních osmi minut provozu zjistila, že reliktní záření je zářením absolutně černého tělesa o teplotě 2,73 K s přesností 10−3. Maximum vyzařování je v okolí jednoho milimetru. V roce 1992 byla objevena anizotropie reliktního záření. Záření je nepatrně teplejší v jednom směru a nepatrně chladnější v opačném směru. Tomu odpovídá naše rychlost pohybu vzhledem k záření 390 km/s. Odečteme-li známý pohyb Slunce kolem středu Galaxie, vychází pro vlastní pohyb naší Galaxie rychlost 600 km/s. Jinak je záření vysoce isotropní. Záření sledované družicí COBE není zcela homogenní. Na mapě intenzity reliktního záření jsou oblasti nepatrně teplejší a oblasti nepatrně chladnější, než je průměr. Odchylky těchto fluktuací od průměrné hodnoty jsou asi 1/100 000. Jde o primordiální fluktuace z období oddělení záření od hmoty, které vedly ke vzniku galaxií. Družice COBE tak přispěla k lepšímu poznání mikrovlnného reliktního záření hlavně dvěma objevy: Objevem anizotropie záření a objevem fluktuací teploty záření. Úhlová rozlišovací schopnost COBE: 7°, teplotní rozlišení 400 μK, tři frekvenční pásma. Autoři experimentů na družici COBE (George Smoot a John Mather) získali Nobelovu za fyziku pro rok 2006.
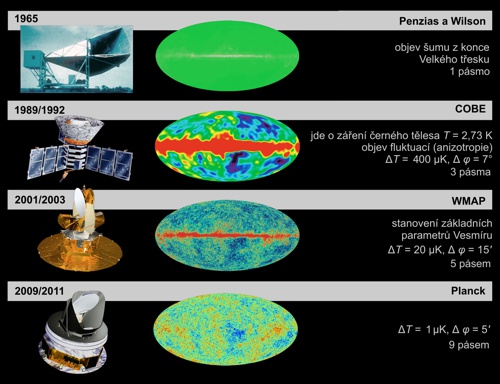
Objev a výzkum reliktního záření. Za lomítkem je rok největšího
úspěchu nebo rok,
v němž byla zveřejněna pozorování.
WMAP (2001)
Americká sonda MAP (Microwave Anisotropy Probe), byla po oznámení prvních výsledků přejmenována na počest Davida Wilkinsona, hlavního autora projektu, na WMAP (Wilkinson Microwave Anisotropy Probe). WMAPWMAP – Wilkinson Microwave Anisotropy Probe, sonda z roku 2001, která pořídila podrobnou mapu fluktuací reliktního záření s úhlovým rozlišením kolem 15′ a citlivostí 20 μK. Zrcadlo sondy mělo rozměry 1,4×1,6 m a teplota chlazené části byla nižší než 95 K. Data sondy jsou důležitým zdrojem informací o raných fázích vývoje vesmíru, většinou se kombinují s daty z pozemských zařízení jako je CBI a ACBAR a s daty z novější sondy Planck. Sonda byla umístěna v Lagrangeově bodě L2 soustavy Země-Slunce, kde pracovala do 28. října 2010. sledovala anizotropii, fluktuace a polarizaci reliktního záření. Úhlové rozlišení sondy bylo 0,3° a teplotní citlivost 20 μK. Sonda pozorovala v pěti oddělených frekvenčních pásmech od 22 do 90 GHz a byla umístěna v blízkosti Lagrangeova bodu L2Lagrangeovy body – pět bodů v sousedství dvou obíhajících hmotných těles, ve kterých je gravitační a odstředivá síla vyrovnána. Polohu těchto bodů poprvé vypočítal italsko-francouzský matematik Joseph-Louis Lagrange. Velmi výhodné je například umístění sond určených k pozorování vzdáleného vesmíru do Lagrangeova bodu L2 soustavy Země-Slunce, který je vzdálený od Země 1 500 000 km ve směru od Slunce (WMAP, Planck, Herschel). Naopak, do bodu L1 soustavy Země-Slunce se umísťují sondy určené pro monitorování Slunce (například SOHO). Lagrangeův bod L3 soustavy Země-Slunce leží opačné straně Slunce, nepatrně dále, než je oběžná dráha Země. Body L4 a L5 neleží na spojnici obou těles, ale tvoří s nimi rovnostranné trojúhelníky. soustavy Země-Slunce, který je vzdálen 1,5 milionů kilometrů od Země. Na stanovišti pracovala od 14. září 2001. Plánovaná délka celé mise byla 27 měsíců (měla zásoby paliva na více než 3 roky): 3 měsíce na let a 24 měsíců na samotné pozorování. První výsledky byly zveřejněny 11. 2. 2003, šlo o natolik přesnou sadu dat, že bylo poprvé možné udělat frekvenční analýzu fluktuací reliktního záření a pomocí ní určit klíčové parametry našeho vesmíru. Detaily naleznete v kapitole Současná kosmologie.
Planck (2009)
Sonda PlanckPlanck – mikrovlnná observatoř evropské kosmické agentury ESA, která byla vynesena do vesmíru 14. května 2009. Byla určena k výzkumu fluktuací reliktního záření a monitorování vesmíru v mikrovlnné oblasti. Měla úhlovou rozlišovací schopnost 5′ a teplotní citlivost 2 μK. Oblohu snímkovala v devíti frekvenčních pásmech od 30 do 857 GHz (0,2 až 10 mm). Zrcadlo sondy mělo rozměry 1,9×1,5 m. Teplotu vysokofrekvenční části ohniska se podařilo po dobu dvou let udržet na extrémně nízké hodnotě 0,1 K. Činnost sondy byla ukončena v říjnu 2013., která byla pojmenována podle německého vědce Maxe Plancka, je nejnovější sondou, která pozorovala reliktní záření. Úhlové rozlišení sondy bylo 5′ a teplotní citlivost 2 μK. Sonda měřila v devíti frekvenčních pásmech (od 30 GHz do 857 GHz, tj. od cca 0,2 mm do 10 mm). Misi uspořádala Evropská kosmická agentura. Sondu Planck (spolu s infračerveným dalekohledem Herschel o průměru zrcadla 3,5 metru) vynesla nosná raketa Arian 5 ECA dne 14. května 2009. Planck pozoroval, stejně jako sonda WMAP, v Lagrangeově bodu L2Lagrangeovy body – pět bodů v sousedství dvou obíhajících hmotných těles, ve kterých je gravitační a odstředivá síla vyrovnána. Polohu těchto bodů poprvé vypočítal italsko-francouzský matematik Joseph-Louis Lagrange. Velmi výhodné je například umístění sond určených k pozorování vzdáleného vesmíru do Lagrangeova bodu L2 soustavy Země-Slunce, který je vzdálený od Země 1 500 000 km ve směru od Slunce (WMAP, Planck, Herschel). Naopak, do bodu L1 soustavy Země-Slunce se umísťují sondy určené pro monitorování Slunce (například SOHO). Lagrangeův bod L3 soustavy Země-Slunce leží opačné straně Slunce, nepatrně dále, než je oběžná dráha Země. Body L4 a L5 neleží na spojnici obou těles, ale tvoří s nimi rovnostranné trojúhelníky. soustavy Země-Slunce. Sonda uskutečnila 4 celé přehlídky oblohy. Chlazení došlo v prosinci 2012. Sonda poskytla dosud nejpřesnější hodnoty parametrů našeho vesmíru, nejpodrobnější mapu fluktuací reliktního záření a vynikající mapu vesmíru v mikrovlnném oboru. Teplotu vysokofrekvenční části ohniska se podařilo po dobu dvou let udržet na extrémně nízké hodnotě 0,1 K. Činnost sondy byla ukončena v říjnu 2013. Data se budou zpracovávat až do roku 2018. Detaily naleznete v kapitole Současná kosmologie. Z frekvenční analýzy vyplynulo stáří vesmíru 13,8 miliardy roků, doba Velkého třesku 380 000 roků a procentuální zastoupení atomární látky (5 %), temné hmoty (27 %) a temné energie (68 %). Z polarizace reliktního záření bylo zjištěno období tvorby prvních hvězd (550 milionů let po vzniku vesmíru).
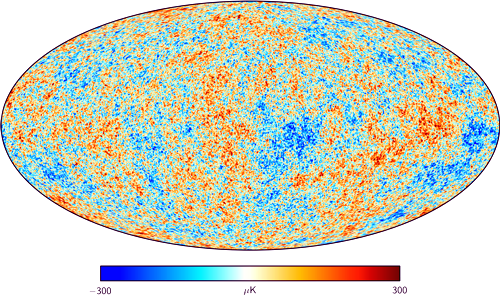
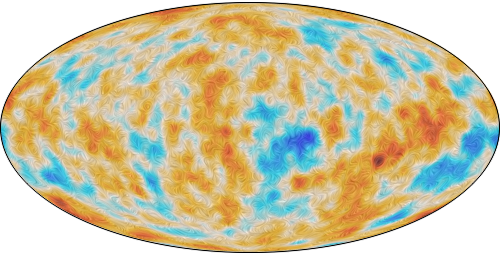
Planck – mapa reliktního záření z roku 2015. V dolní části je
mapa
polarizace reliktního záření z téhož roku..Zdroj: ESA.