
Gravitace | Obecná relativita
Trocha historie
Gravitační interakce se od všech ostatních výrazně odlišuje. Jako jediná působí na všechny částice. Toto působení má zvláštní charakter: Testovací (malá) tělesa se v gravitačním poli pohybují po stejných trajektoriích. Už Galileo Galilei věděl, že doba volného pádu malé kuličky i velkého kamene je v tíhovém poli Země shodná. (Nesmí jít například o pírko, kde je podstatnou silou odpor vzduchu.) To je důsledkem tzv. principu ekvivalence mezi setrvačnou a gravitační hmotou. Hmota se projevuje setrvačnými a gravitačními účinky a ty jsou si úměrné. Nelze proto od sebe odlišit setrvačné a gravitační jevy. Je jedno, zda se nacházíme v urychlovaném výtahu, tj. neinerciální soustavě, nebo v tíhovém poli se stejným gravitačním zrychlením. V obou soustavách dopadnou experimenty stejně. To vedlo Alberta Einsteina k zobecnění speciální relativity platící v inerciálních soustavách na veškeré souřadnicové systémy a ke vzniku obecné relativity, jejíž kostru dokončil v roce 1915.
Právě univerzálnost gravitační interakce a jednotná odezva všech testovacích částic na zdroj gravitačního pole vedla k přehodnocení klasického pojmu síly. Zakřivení trajektorií již není způsobeno těžko definovatelnou silou, ale vlastnostmi času a prostoru. V obecné relativitě sama tělesa zakřivují čas a prostor a v tomto zakřiveném časoprostoru se pohybují po nejrovnějších možných drahách – geodetikách. Například volný pád všech těles probíhá stejně proto, že se pohybují v časoprostoru zakřiveném Zemí a toto zakřivení je pro všechna tělesa stejné. Prostor a čas v obecné relativitě bez samotných těles neexistují. Tělesa sama časoprostor vytvářejí. Zakřivení časoprostoru je matematicky popisováno metrickým tenzorem – jde vlastně o koeficienty gμν v Pythagorově větě, které určují vlastnosti času a prostoru.
| Základní metriky | |
|---|---|
| dl2 = dx2 + dy2 + dz2 | Kartézská metrika – kvadrát vzdálenosti v kartézském souřadnicovém systému. |
| ds2 = −c2dt2 + dx2 + dy2 + dz2 | Minkowského metrika – časoprostorový interval ve speciální relativitě. |
| ds2 = g00dt2 + g11dx2 + g22dy2 + g33dz2 | Riemannova metrika – metrika v obecné relativitě (v ortogonálním systému souřadnic). |
Koeficienty gμν jsou netriviální buď v křivočarých souřadnicích, nebo v křivém časoprostoru. Sám pojem souřadnic v obecné relativitě ustupuje do pozadí, význam mají měřitelné efekty na gravitujících tělesech. Ve čtyřrozměrném časoprostoru existuje 16 koeficientů gμν, ty jsou ale symetrické, takže nezávislých je jich jen 10. Albert Einstein nalezl diferenciální rovnice druhého řádu rovnice pro metrické koeficienty gμν. Své rovnice představil před Pruskou akademií věd na podzim roku 1915. První řešení pro sféricky symetrické gravitační pole kolem centrálního tělesa nalezl Karl Schwarzschild v roce 1916. Jeho řešení ve velké vzdálenosti od zdroje přechází v Minkowského metriku speciální relativity, pohyby těles ve větších vzdálenostech od zdroje jsou shodné s pohyby v Newtonově teorii. V silnějších polích (blíže ke zdroji) je ale v předpovědích možné pozorovat rozdíly. Světelný paprsek se zakřivuje, dráhy těles nejsou uzavřené elipsy, dochází ke stáčení celé trajektorie, hodiny jdou v různých místech gravitačního pole různě a pro vnějšího pozorovatele není možné pozorovat děje pod tzv. Schwarzschildovým poloměrem. Je-li těleso vytvářející pole pod Schwarzschildovým poloměrem, jedná se o černou díruČerná díra – objekt, který kolem sebe zakřiví čas a prostor natolik, že z něho nemůže uniknout ani světlo. Část z nich vzniká kolapsem hvězdy v závěrečných fázích vývoje. Druhou skupinu tvoří obří černé díry sídlící v centrech galaxií. Rotující černé díry kolem sebe vytvářejí akreční disky látky a v ose rotace výtrysky vysoce urychlených částic. Paradoxně akreční disky i výtrysky, vznikající v bezprostředním okolí černé díry, velmi intenzivně vyzařují..
Každé těleso kolem sebe zakřivuje a spoluvytváří jemné
předivo času a prostoru. Zdroj: ESA.
Jiným důležitým řešením rovnic obecné relativity je Fridmanovo řešení z roku 1922, podle kterého nemůže být homogenní izotropní vesmír statický, musí se rozšiřovat nebo smršťovat. Nezávisle řešil Einsteinovy rovnice pro modely vesmíru belgický kněz George Lemaître. Jeho články ale vycházely v místních časopisech a nedostaly se k ostatním kosmologům. Lemaître také navrhl hypotézu prvotního atomu – velmi husté malé oblasti, z níž vznikl celý vesmír. V roce 1948 tuto hypotézu v poněkud jiné podobě rozpracoval americký fyzik George Gamow se spolupracovníky. Pro jeho teorii hustého a horkého původu světa se ujal název Velký třesk.
Z rovnic obecné relativity plyne i mnoho dalších jevů. Hned v roce 1916 Albert Einstein předpověděl existenci gravitačních vln – jemných opakujících se záhybů v předivu časoprostoru, které se pohybují rychlostí světla napříč vesmírem. Přesně po sto letech bylo v roce 2016 oznámeno na mimořádné tiskové konferenci jejich zachycení. Uveďme nyní některé jevy, které obecná relativita předpověděla a které neplynou z Newtonova pojetí gravitace:
- zakřivení světelného paprsku v gravitačním poli (1,75" u povrchu Slunce),
- gravitační čočky (první objevena v roce 1979),
- stáčení perihelia planet (zejména Merkuru, kde jde o 43" za století),
- gravitační červený posuv (změna frekvence fotonů opouštějících těleso),
- zpoždění elektromagnetického signálu,
- kosmologický červený posuv způsobený expanzí vesmíru,
- Lensův-Thirringův jev (strhávání časoprostoru rotujícím tělesem),
- gravitační vlny,
- černé díry,
- rozpínání vesmíru,
- neeukleidovská geometrie časoprostoru.

Osobnosti, které nacházely první řešení nových rovnic
obecné relativity,
nové teorie gravitace: Einstein, Schwarzschild,
Lemaître a Fridman.
Základní principy obecné relativity
| klasická relativita |
Mechanické děje dopadnou ve všech inerciálních soustavách stejně. Žádný z inerciálních systémů není nijak privilegován. |
| speciální relativita |
Mechanické i elektromagnetické děje dopadnou ve všech inerciálních soustavách stejně. Žádný z inerciálních systémů není nijak privilegován. Rychlost světla je ve všech inerciálních soustavách stejná. |
| obecná relativita |
1. Všechny děje dopadnou v libovolném souřadnicovém systému
stejně. Žádný systém není nijak privilegován. 2. Gravitaci a setrvačné děje od sebe nelze odlišit. V urychlující se raketě dochází ke stejným dějům jako ve skutečném gravitačním poli. Naopak ve volně padajícím letadle pociťujeme stav beztíže a gravitační pole nevnímáme. Bohužel jen na chvíli. Vyjádřením tohoto faktu je tzv. princip ekvivalence. |
| (slabý) princip ekvivalence |
Setrvačná a gravitační hmotnost jsou si navzájem úměrné, při vhodné volbě jednotek jsou si rovné. Princip ekvivalence vede k nerozlišitelnosti setrvačných a gravitačních jevů a umožňuje popisovat gravitaci za pomocí křivého časoprostoru. |
| silný princip ekvivalence |
Energie odpovídající elektromagnetickému poli se také projevuje jako setrvačná hmotnost. I tato hmotnost má své gravitační účinky. |
| velmi silný princip ekvivalence |
Energie, která by odpovídala samotnému gravitačnímu poli, má také projevy jako setrvačná a gravitační hmotnost. |
| matematický popis OTR |
1. Každé těleso zakřivuje prostor a čas kolem sebe. 2. V tomto pokřiveném světě se tělesa pohybují po nejrovnějších možných drahách (geodetikách). Tělesa časoprostor sama vytvářejí, bez nich časoprostor neexistuje a nemá smysl. |
Princip ekvivalence
Hmotnost lze určovat ze setrvačných účinků těles (schopnosti setrvávat v daném pohybovém stavu) nebo z gravitačních účinků (schopnosti všech těles se přitahovat). Z experimentů se ukazuje, že obě hmotnosti jsou si úměrné a při vhodné volbě jednotek rovné. V Newtonově gravitačním zákonu se potom setrvačná hmotnost pokrátí s gravitační hmotností tělesa (například pro volný pád platí ms d2y/dt2 = mg g) a všechna tělesa se budou pohybovat po stejných trajektoriích. V malé volně gravitující kleci (padající výtah) se proto tělesa chovají jako ve stavu beztíže a naopak v urychlované kleci se tělesa chovají jako v tíhovém poli. V prostorově malé kleci v dosti krátkém časové okamžiku nerozlišíme gravitační a setrvačné efekty. Hledaný inerciální systém, ve kterém platí zákony speciální teorie relativity, lze realizovat jako po krátkou dobu volně gravitující (padající) klec malých rozměrů. Jde o tzv. lokální inerciální systém (LIS). Nejlépe snad lze zavedení LIS pochopit v experimentu Harolda Waaga. Představme si tři propojené rovnoběžné desky s otvory na přímce. K první desce je připojeno zařízení vrhající kuličku, k poslední vak, který ji zachytí. Je-li zařízení v klidu vzhledem k povrchu Země (stojí na Zemi, visí na laně), kulička díky tíhovému poli neprojde až do vaku. Je to tím, že systém není inerciální a tělesa se nepohybují rovnoměrně přímočaře. Přestřihneme-li závěs a zařízení bude padat volným pádem, stává se lokálním inerciálním systémem (LIS), tělesa se pohybují rovnoměrně příločaře a kulička dopadne do záchytného vaku.
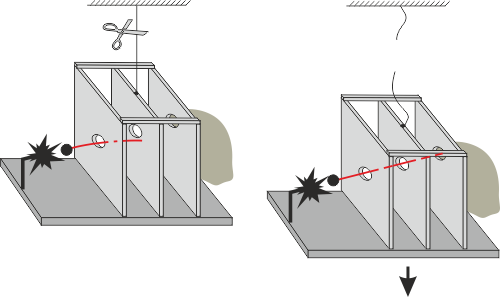
Experiment Harolda Waaga ukazuje jednoduchou realizaci lokální inerciální soustavy.
Princip ekvivalence byl poprvé ověřen v experimentech, které prováděl maďarský fyzik baron Loránd Eötvös od roku 1885. Nejpreciznější experimenty uskutečnil v letech 1906 až 1909. Dvě tělesa umístnil na konce vodorovného ramene. Celé rameno pak viselo na torzním vlákně. Na tělesa působila jak gravitační síla Země (ta reaguje na gravitační hmotnost), tak odstředivá síla (ta reaguje na setrvačnou hmotnost). Pokud by obě hmotnosti nebyly stejné (nebo alespoň sobě úměrné), na zavěšená tělesa by působil krutný moment, který by pootočil závěsem. V experimentech Eötvös spolu s dalšími kolegy prokázal rovnost gravitační a setrvačné hmotnosti s relativní přesností 10−9. Experimenty byly v různých variantách (například působení Slunce na dvojici těles Země-Měsíc) mnohokrát zopakovány a dosud nejvyšší relativní přesnosti (10−15) by mělo být vbrzku dosaženo při experimentu na palubě francouzského mikrosatelitu MICROSCOPE (Micro-Satellite à traînée Compensée pour l'Observation du Principe d'Equivalence) v roce 2017, viz AB 17/2017).

Příprava mikrosatelitu MICROSCOPE v laboratořích francouzské kosmické agentury CNES v Toulouse. Testován je volný pád dvou těles různého složení (jedno je z titanu a druhé ze slitiny platiny a rhodia). Mikrosatelit startoval dne 2. května 2016 a měl by fungovat dva roky. Zdroj: CNES.
Stavba obecné relativity
Tělesa pohybující se pod vlivem gravitačních polí se díky ekvivalenci setrvačné a gravitační hmotnosti pohybují po stejných trajektoriích (pokud je jejich vlastní pole zanedbatelné). Například cihla a malá kulička padající ze stejné výšky dopadnou na zem za stejný čas. To přivedlo Alberta Einsteina k myšlence, že křivost trajektorií je vlastností samotného prostoru a času. Prostor a čas je zakřiven a tělesa se pohybují po rovných drahách v tomto křivém prostoru (lépe časoprostoru, časovou souřadnici nikdy ze svých úvah nemůžeme vynechat). Dva kameny na následujícím obrázku se podle newtonovské teorie potkají proto, že Slunce na ně působí gravitační silou, která zakřivuje jejich dráhu v prostoru. Podle obecné relativity se oba kameny pohybují po „přímkách“, ale v křivém čase a prostoru. Zakřivení času a prostoru samozřejmě způsobuje Slunce.

Zakřivení třídimenzionálního prostoru si můžeme jen dosti těžko představit. Celkem bez problému si ale představíme zakřivenou dvojdimenzionální plochu (povrch jablka, míče, sedlo koně, reliéf krajiny). Nejkratší spojnicí dvou bodů na takto zakřivené ploše již není přímka. Je to křivka, kterou nazýváme geodetika. Jak si ale představit zakřivení v čase? Kupodivu je to velmi jednoduché. Zakřivení časové osy vlastně neznamená nic jiného než různý chod hodin v různých místech. Různě vysoko nad povrchem Země jdou hodiny různě. Na časovou osu nesmíme nikdy zapomínat. Ukažme si to na jednoduchém příkladě: Z nějakého místa na povrchu Země hodíme kámen a poté pod menším úhlem vystřelíme střelu tak, aby obě tělesa dopadla stejně daleko. Na první pohled se zdá, že něco je špatně. Prostor je zakřiven přítomností Země, a tak by se kámen i střela měly pohybovat po stejných křivkách. Zapomněli jsme ale na časovou osu. Na obrázku vpravo je stejná situace zakreslena i s časem. Vidíme, že kámen i střela se pohybují různými místy časoprostoru. Jestliže na časové a prostorových osách zvolíme stejné jednotky (to lze zařídit například tak, že místo času budeme používat kombinaci ct), zjistíme, že obě trajektorie mají v časoprostoru stejnou křivost.
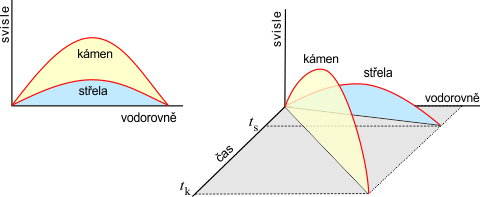
- Každé těleso zakřivuje prostor a čas kolem sebe (prostor i čas!).
- Tělesa se pohybují v křivém světě po geodetikách (nejrovnějších drahách).
Matematické zpracování postulátů OTR může být značně obtížné, využívá se poznatků z diferenciální geometrie a problémy gravitace se převádějí na geometrické vlastnosti prostoru a času. Nicméně základní myšlenky OTR jsou jednoduché a přímočaré.
Jaký je vztah mezi obecnou a speciální relativitou? Obecná relativita platí v jakémkoli souřadnicovém systému, třeba zrychleném, rotujícím a podobně. Speciální relativita platí jen v inerciálních systémech. Ty, jak víme, existují jen lokálně. Lze je vybudovat jako klece malých rozměrů volně padající v prostoru po krátkou dobu. Chceme-li například sledovat pohyb světelného paprsku v blízkosti Slunce v rámci speciální relativity, musíme v každém místě, do kterého se paprsek dostane, vybudovat LIS, v něm pohyb vyřešit (uvnitř LIS je to pohyb po přímce, ale celá klec padá volným pádem, a pro vnějšího pozorovatele je proto trajektorie paprsku zakřivena). Přejdeme k dalšímu LIS, opět pohyb vyřešíme atd. Výsledný pohyb bude integrací pohybů v jednotlivých LIS. Pomocí rovnic obecné relativity můžeme najít přímo řešení celého pohybu bez zavádění lokálně inerciálních systémů.
Zakřivení prostoru a času
V zakřiveném prostoru (například na povrchu koule) již neplatí známé vztahy z Eukleidovské geometrie. Součet úhlů v trojúhelníku není 180°, obvod kružnice není 2πr, plocha koule není 4πr2, čtyři kolmé přímky nevytvoří obdélník, atd. Důsledkem zakřivení prostoru kolem našeho Slunce je například stáčení perihélia Merkuru a odklon světelného paprsku hvězd od přímky. Kdybychom měřili poloměr Slunce ze skutečných radiálních měření, bude se nalezená hodnota lišit v důsledku zakřivení prostoru od hodnoty získané z měření plochy povrchu Slunce, r = (S/4π)1/2, o šestinu Schwarzschildova poloměru, což činí 0,5 kilometru. Dalším projevem zakřivení prostoru jsou gravitační čočky. Hmotný objekt ležící mezi zdrojem záření a pozorovatelem zakřivuje světelné paprsky podobně jako skleněná čočka v laboratoři.
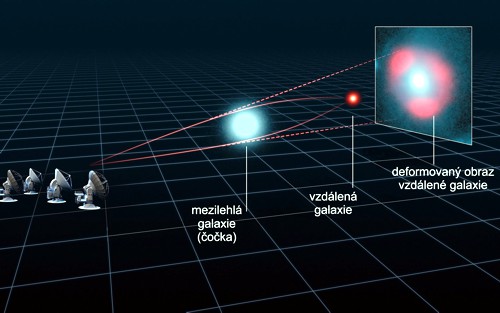
Princip gravitační čočky. Zdroj: ALMA.
Zakřivení času znamená, že hodiny jdou v různých místech různě. Zakřivení času v okolí naší Země bylo poprvé měřeno už v roce 1960, jako hodiny tenkrát posloužily fotony vysílané radioaktivním kobaltem 60C. Měření zakřivení času je věnován bulletin AB 10/2010. V současnosti se se zakřivením času naší Zemí asi nejčastěji setkáme při používání polohovacího zařízení GPSGPS – globální polohovací systém, navigace pomocí družic umístěných na oběžné dráze Země. Oficiální název je NAVSTAR GPS (Navigation Satellite Timing and Ranging Global Positioning System). Systém je vyvíjen 30 let a v roce 2007 byla na oběžné dráze umístěna již čtvrtá generace polohovacích družic. v automobilu. V našem autě jde čas jinak než na družici nacházející se ve výšce 20 000 km, se kterou náš přijímač komunikuje. Pokud by nedošlo k přepočtení obou časů, rozešla by se v naší zeměpisné šířce určovaná poloha od skutečné za 24 hodin o celých 8 kilometrů. Některé nesymetrické objekty mohou dokonce generovat periodické zakřivení času a prostoru, které se od nich šíří v podobě gravitační vlny. Gravitační vlny byly poprvé zachyceny v roce 2015 (viz AB 6/2016) Detaily o hledání gravitačních vln naleznete na stránce Testy obecné relativity.

Gravitační vlny jsou jemné záhyby časoprostoru šířící se
rychlostí světla.
Zdroj: Pierre Binétruy, APC, Paris.
Některé užitečné vztahy
| Δω/ω0 = –Δλ/λ0 = Δϕ/c2 | Změna frekvence fotonu způsobená změnou gravitačního potenciálu ϕ. V tíhovém poli je Δϕ = gΔl. |
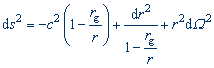 |
Schwarzschildova metrika. Tvar intervalu ve sférických souřadnicích v okolí sféricky symetrického tělesa. |
| rg = 2GM/c2 | Schwarzschildův poloměr. Poloměr, z pod kterého se od hmotného tělesa nemůže vzdálit ani světlo |
| M, L, Q = const | „No hair“ teorém. Černá díra si ponechává jen informaci o hmotnosti, momentu hybnosti a náboji |
| ΣSk(t) ≤ ΣSk(t+Δt) | Termodynamika černých děr. Ať probíhají jakékoli procesy včetně spojování černých děr, celkový povrch se nezmenší. Povrch černé díry v jistém smyslu představuje pojem entropie klasického souboru částic |
| Fridmanova-Lemaitre-Robertsonova-Walkerova metrika rozpínajícího se vesmíru | |
| H2 – 8/3 πGρ = –c2k/a2 | Einsteinova-Fridmanova rovnice. Diferenciální rovnice pro expanzní funkci a(t). Veličina k je křivost vesmíru. |
| H ≡ (da/dt)/a | Hubblova konstanta. Udává koeficient úměrnosti mezi rychlostí rozpínání vesmíru a vzdáleností objektu. Z pozorování: H ~ (68±4) km s−1 Mpc−1. |
| ρC = 3H2/(8πG) | Kritická hustota. Hustota, při níž se ve Fridmanově řešení mění otevřený (stále se rozpínající) vesmír na uzavřený (v budoucnu kolabující). |
| z = Δλ/λ0 = [a(t) – a(t0)]/a(t0) | Kosmologický posuv. Změna frekvence vyzařovaného světla způsobená změnou geometrie prostředí, kterým se světlo šíří, tedy rozpínáním vesmíru. |
