Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie.
Vydavatel: AGA (Aldebaran Group for Astrophysics)
Číslo 8 – vyšlo 10. března, ročník 16 (2018)
© Copyright Aldebaran Group for Astrophysics
Publikování nebo šíření obsahu je zakázáno.
ISSN: 1214-1674,
Email: bulletin@aldebaran.cz

Titius s Bodem opět na scéně?

Rudolf Mentzl

Hledání řádu vesmíru provází lidstvo již od nepaměti. Již staří Řekové… Tenkrát to byla spíš přírodní filosofie, než pokusem a výpočtem podložená fyzika, proto nechme staré Řeky spát a mladé odpočívat. Přeskočme i přelom středověku a novověku, kdy Johannes Kepler dokázal mezi sféry šesti tehdy známých planet vložit platónská tělesa, což je fakt sám o sobě pozoruhodný, ale těžko uchopitelný.

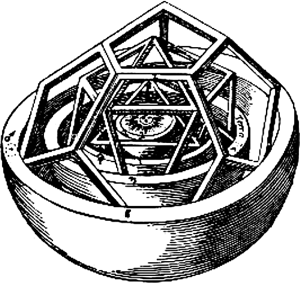
Keplerův model Sluneční soustavy složený z platónských těles

Středy platónských těles jsou totožné se středem našeho Slunce. Přitom je každé těleso opsáno dráze jedné planety a vepsáno do dráhy planety následující. Na rytině je zobrazena vnitřní část modelu používaného Johannem Keplerem.

Titiovo-Bodeovo pravidlo – matematické pravidlo vyjadřující přibližnou vzdálenost planet od Slunce. Jeho předpis zní: a = 0.4 + 0.3×2ⁿ, kde a je velikost hlavní poloosy vyjádřená v astronomických jednotkách a za n postupně dosazujeme hodnoty −∞, 0, 1, 2, …. Pravidlo dobře popisuje polohy planet s výjimkou Neptunu. Také předpovídá mezeru mezi Marsem a Jupiterem obsazenou hlavním pásem planetek.

Titiovo-Bodeovo pravidlo

V osmnáctém století byla již fyzika pokročilá a její popis drah planet Sluneční soustavy se podobal tomu dnešnímu. Dráhy byly změřeny a propočteny poměrně přesně, zákony nebeské mechaniky fungovaly bezvadně, pouze nikdo nedokázal odpovědět na otázku, proč planety obíhají právě tam, kde obíhají (což nevíme dodnes). Hledání řádu planetárních drah pokračovalo. Koncem století zjistili německý matematik Johann Daniel Titius a o pár let později ředitel berlínské hvězdárny Johann Elert Bode, že vzdálenosti planetPlaneta – nebeské těleso, které: 1) obíhá okolo Slunce. 2) má dostatečnou hmotnost, aby jeho gravitace překonala vnitřní síly pevného tělesa (dosáhne kulového tvaru odpovídajícího hydrostatické rovnováze). 3) vyčistí okolí své dráhy od drobnějších těles. Planetami jsou Merkur, Venuše, Země, Mars, Jupiter, Saturn, Uran a Neptun. V poslední době se název planeta vžil i pro exoplanety obíhající kolem jiných hvězd, než je naše Slunce. od SlunceSlunce – nám nejbližší hvězda, tzv. hvězda hlavní posloupnosti, která se nachází ve vzdálenosti 149,6×10⁶ km od Země. Jde o žhavou plazmatickou kouli s průměrem 1,392×10⁶ km, teplotou na povrchu 5 780 K, teplotou v centru přibližně 15×10⁶ K a zářivým výkonem 3,846×10²⁶ W. Zdrojem energie je jaderná syntéza, při které se za každou sekundu sloučí v jádru Slunce 700 milionů tun vodíku na hélium. víceméně respektují jakési matematické pravidlo, později nazvané právě po nich. Pokud bychom si vynesli do grafu velikosti hlavních poloos planet Sluneční soustavy, asi bychom si na první pohled všimli, že je to relativně hladká křivka připomínající exponenciálu. V tomto smyslu také zní Titiovo-Bodeovo pravidlo: a = 0.4 + 0.3×2ⁿ. Pokud za n dosazujeme hodnoty −∞, 0, 1, 2, …, dostaneme vzdálenosti planet od Slunce v astronomických jednotkáchAstronomická jednotka – au (astronomical unit), původně střední vzdálenost Země od Slunce, v roce 2012 ji IAU definovala jako 149 597 870 700 m přesně a změnila zkratku z AU na au. Astronomická jednotka se používá především pro určování vzdáleností ve sluneční soustavě, pro přibližné odhady postačí hodnota 150 milionů kilometrů..

Nějakých deset let po publikování pravidla objevil anglický astronom Frederick William Herschel planetu UranUran – jedna ze čtyř obřích planet, sedmá planeta sluneční soustavy má charakteristický modrozelený nádech. Průměrná hvězdná velikost 5,5^m je na hranici viditelnosti lidským okem. Planeta má soustavu prstenců a kolem krouží rozsáhlý systém měsíců podobně jako u ostatních obřích planet. Kromě vodíku a helia obsahuje atmosféra také metan, způsobující namodralé zbarvení. Ve středu Uranu je jádro z hornin a železa. Rotační osa Uranu je vzhledem k rovině oběhu stočená na bok (98°), patrně díky střetu s jinou velkou planetou při vzniku sluneční soustavy. Rotace je diferenciální s periodou 16÷17 hodin. Rychlost větrů v atmosféře dosahuje až 600 km/h. Magnetická osa svírá s osou rotace úhel 59° a je značně excentrická (prochází 8 000 km od středu planety). Magnetosféra je výrazná, intenzita pole je srovnatelná s intenzitou pole Země, ohon je zkroucen do tvaru vývrtky díky vlastní rotaci planety.. Velká poloosa Uranu činí 19.2 au, Titiovo-Bodeovo pravidlo předvídá 19.6 au, což je poměrně dobrá shoda, dá se bezmála říci triumf teorie. O dvacet let později dochází k objevu planetky CeresCeres – trpasličí planeta mezi drahou Marsu a Jupiteru. Objevena byla v roce 1801 Giuseppem Piazzim. Průměr má 974 kilometrů. Pojmenována je po římské bohyni úrody. Slunce oběhne jednou za 4,6 roku ve vzdálenosti 2,5÷3 AU. (považované tenkrát za planetu) ve vzdálenosti 2.76 au, tedy jen 0.4 au menší než vzdálenost vycházející z pravidla. Později byl sice planetce Ceres status planety odepřen, ale podle dalšího materiálu, který se v těchto místech nachází, si dovedeme představit, že se tu nějaká planeta zformovat mohla. Po objevu planety NeptunNeptun – poslední z obřích planet. Podobně jako ostatní obří planety má prstence, rozsáhlou soustavu měsíců a pásovitou strukturu atmosféry s obřími víry – skvrnami. Neptun je téměř stejně velký jako Uran. Průměrná hvězdná velikost je 7,8^m, a proto nemůže být pozorován okem. Atmosféra má pásovitou strukturu, rotace je diferenciální s průměrnou periodou 19 hodin. Vlastní rotační perioda planety je 16 hodin, atmosféra tedy vzhledem k povrchu rotuje retrográdně. V atmosféře se nachází obří anticyklóny, například Malá a Velká temná skvrna. Atmosféra má zelenomodrou barvu, v horních vrstvách převládá vodík a helium. Modrozelené zabarvení je způsobeno stopami metanu. Rychlosti větru naměřené sondou Voyager 2 přesahují 2 000 km/h. Magnetické pole má dipólový charakter, osa je skloněna 47° vzhledem k rotační ose a posunutá od středu o 0,55 poloměru. sláva Titiova-Bodeova pravidla pohasla, tato planeta se do řady hodí jen přibližně. Kromě toho již od začátku zlobil Merkur, kde bylo třeba za n dosazovat −∞. Především však není zřejmé, jaký mechanismus by nutil planety obíhat ve vzdálenostech daných nějakým vzorcem. Po nějaké době převládlo přesvědčení, že se jedná nejspíš o náhodu, podobně jako planetární sféry vepsané do platónských těles.

Bez zajímavosti však není fakt, že podobný vzorec se dá sestavit také pro některé měsíce velkých planet. Zde jsou astronomové na rozpacích. Měsíců je sice dost, ale možná až příliš, některé jsou jen zachycené planetky. Aby vztahy lépe vypadaly, sdružují přívrženci myšlenky některé měsíčky do skupin, což je v mnoha případech minimálně námět na dlouhou diskuzi. Přesto mějme na paměti, že exponenciální závislost velikosti hlavních poloos vykazují například galileovské měsíce JupiteruJupiter – největší a nejhmotnější (1,9×10²⁷ kg) planeta Sluneční soustavy má plynokapalný charakter a chemické složení podobné Slunci. Se svými mnoha měsíci se Jupiter podobá jakési „sluneční soustavě“ v malém. Jupiter má, stejně jako všechny obří planety, soustavu prstenců. Rychlá rotace Jupiteru (s periodou 10 hodin) způsobuje vydouvání rovníkových vrstev a vznik pestře zbarvených pásů. Charakteristickým útvarem Jupiterovy atmosféry je Velká rudá skvrna, která je pozorována po několik století. Atmosféra obsahuje kromě vodíku a helia také metan, amoniak a vodní páry. Teplota pod oblaky směrem ke středu roste. Na vrcholcích mraků je −160 °C, o 60 km hlouběji je přibližně stejná teplota jako na Zemi. Proudy tekoucí v nitru (v kovovém vodíku) vytvářejí kolem Jupiteru silné dipólové magnetické pole..

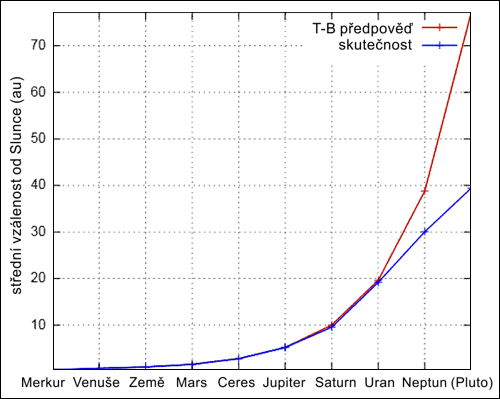
Velikosti hlavních poloos vynesené do grafu jasně ukazují na exponenciální závislost.
Zdroj: Krishnavedala.

Současné představy

Dnes je situace poněkud jiná. Velký pokrok v objevování exoplanet problém Titiova-Bodeova pravidla znovu otevřel. K dispozici máme stovky planet s planetárními systémy s více než třemi planetami. V roce 2013 se Steffen Kjar Jacobsen (Institut Niesle Bohra v Kodani) a Charles Lineweaver s Timothy Bovairdem (Australská národní univerzita) rozhodli na těchto datech zákonitost nejen prozkoumat, ale i využít k hledání dalších planet. Začátky byly povzbuzující, ze 151 zkoumaných planetárních systémů plných 124 vykazovalo exponenciální závislost ve velikostech poloos. Výzkumný tým však šel ještě dále, navázal na dřívější práce pánů Francoise Granera (Ecole Normale Superieure, Paříž) a Berengera Dubrulla (Observatoire Midi Pyrenees, Toulouse) a sestavil prioritní seznam k vyhledávání dalších planet. Ze zkoumaného vzorku 151 systémů jich 27 nesplňovalo žádnou závislost. Respektive, závislost by vykazovalo, ale posloupnosti planet vykazovaly jakési díry v rozestupu. Právě v těchto děrách doporučovali hledat podrobněji.

Předpokládali objev 77 planet ve čtyřiceti planetárních systémech, objeveno jich však bylo pouze pět. K tomuto nepříliš výraznému úspěchu se přidala skepse ohledně systémů se třemi planetami, které sice vykazovaly exponenciální závislost, ale je třeba si uvědomit, že takové nepočetné systémy poskytují hodně místa pro náhodu a už vůbec nedokazují, že se jedná právě o exponenciální řadu.

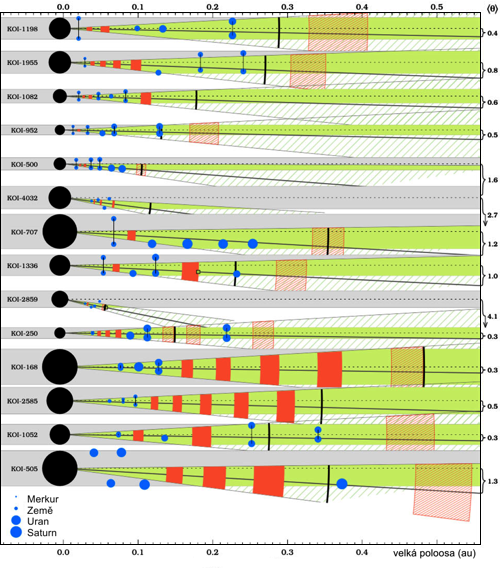
Modifikované Titiovo-Bodeovo pravidlo ve vybraných exoplanetárních soustavách. Modře jsou zobrazeny již objevené planety, červené pruhy jsou v místech dalších předpokládaných planet. Zdroj: INB/ANU.

Události minulého roku zájem o Titiovo-Bodeovo pravidlo opět vzkřísily. Jedná se o analýzu dat nedávno objeveného systému Trappist-1. Je to mediálně asi nejúspěšnější systém. Kolem červeného trpaslíka tu obíhá sedm kamenných planet. Je až zarážející, jak přesně jejich rozestupy sledují exponenciálu. Poměry mezi poloosami sousedních planet se jen nepatrně odchylují od průměrné hodnoty 1.328. Vzdálenosti od centrální hvězdy poměrně dobře vystihuje vztah: a = α×βⁿ, kde α = 8.7 a ß = 1.328.

planeta	velká poloosa (10⁻³ au)	α×βⁿ
b	11.11±0,34	11.55
c	15.21±0,47	15.34
d	21.44_−0.63^+0,66	20.38
e	28.17_−0.87^+0,83	27.06
f	37.1±1,1	35.93
g	45.1±1,4	47.72
h	63_-13+²⁷	63.37

Velikosti hlavních poloos planet systému Trappist-1. V druhém sloupci je naměřená
vzdálenost, ve třetím hodnota předpokládaná matematickým předpisem.

Vladimir Pletser (Technology and Engineering Center for Space Utilization, Chinese Academy of Sciences) a Lorenzo Basano (Universita degli Studi di Genova) šli v analýze ještě dále. Zajímalo je, zda by bylo možné proložit podobnou křivku také oběžnými dobami planet. Na to se dá samozřejmě odpovědět rovnou, i bez analýzy. Z Keplerova zákona plyne hodnota parametru β_T = β_a^3/2, tedy zhruba 1.53. Tato hodnota vzbudila oprávněný zájem. Je totiž velice blízká rezonančnímu poměru 3:2. Jedná se však o hodnotu průměrnou. V. Pletsera a L. Basana zajímalo, jaké budou konkrétní hodnoty.

Trappist-1	Oběžná doba(dny)	T_i/T_i-1
b	1.51087081 ±6×10^-7	–	–
c	2.4218233 ±1.7×10^-6	1.602932087 ±1.8×10^-6	8/5
d	4.049610 ±6.3×10^-5	1.672132727 ±2.7×10^-5	5/3
e	6.099615 ±1.1×10^-5	1.506222821 ±2.6×10^-5	3/2
f	9.206690 ±1.5×10^-5	1.509388707 ±5.2×10^-6	3/2
g	12.35294 ±1.2×10^-4	1.341735195 ±1.5×10^-5	4/3
h	20₋₆⁺¹⁵	1.62_−0.5^+1.2	9/8 < 13/8 < 17/6

Oběžné doby planetárního systému Trappist-1. Ve třetím sloupci je poměr oběžné doby sousedních planet. Ve čtvrtém pak tentýž poměr vyjádřený v poměru malých čísel. Měření v posledním řádku je značně nepřesné. Zdroj: Vladimir Pletser.

Autoři, aniž by chtěli spekulovat o fyzikální zákonitosti, upozorňují na čísla v posledním sloupci, která odpovídají Fibonacciho posloupnosti. Rozhodnout, zda je to náhoda, nebo projev skrytého pravidla, je v tuto chvíli předčasné. Rezonanční poměry v malých hodnotách přirozených čísel však nutí k zamyšlení, zda to není obecný důsledek formování planetárního systému.

Odkazy