|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Jak stará je sluneční soustava?
Jakub Rozehnal
Astronomové soudí, že stáří naší sluneční soustavy je přibližně 4,56 miliardy let. Přesnost, s jakou se na tomto údaji shodují, je přitom obdivuhodná – pouhých 10 milionů let. Jak je možné určit stáří sluneční soustavy s takovou přesností?
K odhadu stáří sluneční soustavy potřebujeme geologicky primitivní, nemetamorfovaný materiál, jaký vznikl přímou akrecí z prachoplynného disku, jenž vznikl společně se SluncemSlunce – nám nejbližší hvězda, tzv. hvězda hlavní posloupnosti, která se nachází ve vzdálenosti 149,6×106 km od Země. Jde o žhavou plazmatickou kouli s průměrem 1,392×106 km, teplotou na povrchu 5 780 K, teplotou v centru přibližně 15×106 K a zářivým výkonem 3,846×1026 W. Zdrojem energie je jaderná syntéza, při které se za každou sekundu sloučí v jádru Slunce 700 milionů tun vodíku na hélium. a nebyl dále přeměněn působením vysokých tlaků či teplot, jaké panovaly v pláštích či jádrech planetárních embryí. Postupným nabalováním prachových zrn o velikosti v řádu desetin mikrometru a jejich „lepením“ elektrostatickými silami mohly již během jedno roku okolo Slunce obíhat částice velikosti štěrku. Samotná doba akrece planetesimálPlanetesimály – tělesa z raných fází vývoje sluneční soustavy. Jedná se o stavební kameny budoucích planetek, na kterých docházelo k procesům diferenciace hmoty a vzniku minerálních asociací typických pro jednotlivé druhy většiny známých meteoritů. V současné době se planetesimály mohou nacházet v oblastech Kuiperova pásu a Oortova oblaku, kam byly vypuzeny v pozdních fázích vývoje sluneční soustavy planetami. o průměru do 1 km tak trvala zřejmě méně než 100 000 let, což je doba velmi krátká s ohledem na přesnost určení stáří celé soustavy.

Umělecká vize vzniku sluneční soustavy. Zdroj: CG Society/Ralf Schoofs.
|
Meteorit kamenný – nejběžnější skupina meteoritů tvořená převážně silikátovými minerály. Tvoří 94 % všech známých meteoritů dopadlých na Zemi. 84 % kamenných meteoritů tvoří tzv. chondrity – chemicky primitivní hmota, která se svým obsahem chemických prvků (mimo lehké prvky) blíží složení sluneční fotosféry, a tedy i složení materiálu ze kterého vznikala sluneční soustava. 8 % tvoří tzv. achondrity – meteority vzniklé obvykle kompletním přetavením chondritů. Zvláštní skupiny achondritů tvoří lunární a marsovské meteority a diferencované meteority nejasného postavení. Planetesimály – tělesa z raných fází vývoje sluneční soustavy. Jedná se o stavební kameny budoucích planetek, na kterých docházelo k procesům diferenciace hmoty a vzniku minerálních asociací typických pro jednotlivé druhy většiny známých meteoritů. V současné době se planetesimály mohou nacházet v oblastech Kuiperova pásu a Oortova oblaku, kam byly vypuzeny v pozdních fázích vývoje sluneční soustavy planetami. Planetka – nesprávně asteroid, malé těleso o rozměrech maximálně stovek kilometrů na samostatné dráze kolem Slunce. Nejvíce planetek se nachází v tzv. Hlavním pásu mezi drahami Marsu a Jupiteru. Obdobná tělesa jsou i v Kuiperově pásu za drahou Neptunu. Trpasličí planeta – nebeské těleso, které: 1) obíhá okolo Slunce. 2) má dostatečnou hmotnost, aby jeho gravitace překonala vnitřní síly pevného tělesa (dosáhne přibližně kulatého tvaru odpovídajícího hydrostatické rovnováze). 3) není satelitem jiného tělesa. 4) nevyčistí okolí své dráhy od drobných těles (na rozdíl od planety). K typickým trpasličím planetám patří velká tělesa Kuiperova pásu, z nichž nejznámější je Pluto. Planeta – nebeské těleso, které: 1) obíhá okolo Slunce. 2) má dostatečnou hmotnost, aby jeho gravitace překonala vnitřní síly pevného tělesa (dosáhne kulového tvaru odpovídajícího hydrostatické rovnováze). 3) vyčistí okolí své dráhy od drobnějších těles. Planetami jsou Merkur, Venuše, Země, Mars, Jupiter, Saturn, Uran a Neptun. V poslední době se název planeta vžil i pro exoplanety obíhající kolem jiných hvězd, než je naše Slunce. |
Nejstarší horniny
Nejstarší horniny, které byly nalezeny na Zemi, utuhly přibližně před 4 miliardami let, starší horniny musíme hledat ve vesmíru. Naštěstí nám zcela zdarma padají na hlavu, a to v podobě jednoho konkrétního typu meteoritů, které nesou souhrnné označení uhlíkaté chondrity. Ani materiál těchto geologicky primitivních těles však nemá všude stejné stáří. Nejstarší částí uhlíkatých chondritůMeteorit kamenný – nejběžnější skupina meteoritů tvořená převážně silikátovými minerály. Tvoří 94 % všech známých meteoritů dopadlých na Zemi. 84 % kamenných meteoritů tvoří tzv. chondrity – chemicky primitivní hmota, která se svým obsahem chemických prvků (mimo lehké prvky) blíží složení sluneční fotosféry, a tedy i složení materiálu ze kterého vznikala sluneční soustava. 8 % tvoří tzv. achondrity – meteority vzniklé obvykle kompletním přetavením chondritů. Zvláštní skupiny achondritů tvoří lunární a marsovské meteority a diferencované meteority nejasného postavení. jsou takzvané vápenato-hlinité inkluze (CAI), které obsahují nejméně těkavé složky původního protoplanetárního disku, jež kondenzovaly při vysokých teplotách (nad 1 300 K). Jejich stáří lze určit různými radiometrickými metodami, jejichž princip si nyní vysvětlíme.
Některé izotopy prvků, o které byla sluneční pramlhovina obohacena výbuchy supernovSupernova – rozmetání podstatné části hvězdy, při kterém vznikne extrémně jasný objekt, jehož svítívost se o více než 4 řády zvýší. Minimálně 10 % hmotnosti původní hvězdy se přemění na energii exploze. Svítivost posléze klesá v průběhu týdnů či měsíců. K tomuto konci vedou dvě možné cesty: 1) jedná se o velmi hmotnou hvězdu, která ve svém jádře vyčerpala zásoby paliva a začala se hroutit pod silou své vlastní gravitace na neutronovou hvězdu, nebo černou díru; 2) jedná se o bílého trpaslíka, který nahromadil materiál od svého hvězdného průvodce, dosáhl Chandrasekharovy meze a prodělal objemovou termonukleární explozi. (viz například AB 9-11/2012), nejsou dlouhodobě stabilní a podléhají radioaktivnímu rozpadu. Příkladem takového procesu může být ?-rozpad, při kterém jádro nestabilního nukliduNuklidy – druhy atomových jader, určené počtem protonů a neutronů. Významem odpovídají izotopům chemických prvků. odštěpí částici ?, tedy héliové jádro se dvěma protonyProton – částice složená ze tří kvarků (duu) se spinem 1/2, hmotností 1,673×10−27 kg (938 MeV) a elektrickým nábojem +1,6×10−19 C. Proton je na běžných časových škálách stabilní, pokud se rozpadá, je poločas rozpadu větší než 1035 let. Za objevitele protonu je považován Ernest Rutherford, který v roce 1911 objevil atomové jádro při analýze rozptylu částice alfa pronikající tenkou zlatou fólií. Samotná jádra vodíku (protony) detekoval v roce 1918 při ostřelování dusíku částicemi alfa. Antiproton byl objeven v roce 1955 Emilio Segrem a Owenem Chamberlainem. a dvěma neutronyNeutron – částice složená ze tří kvarků (ddu) se spinem 1/2, hmotností 1,675×10−27 kg (940 MeV) a nulovým elektrickým nábojem. Volné neutrony jsou nestabilní se střední dobou života 886 s (15 minut) a poločasem rozpadu 10 minut. V roce 1930 Walther Bothe a Herbert Becke ostřelovali lehké prvky alfa částicemi a objevili nový druh pronikavého záření. V roce 1932 zjistil James Chadwick, že je toto záření složeno z neutrálních částic přibližné velikosti protonu a objevil tak neutron.. Protonové čísloProtonové číslo Z – udává počet protonů v atomovém jádře prvku. nukliduNuklidy – druhy atomových jader, určené počtem protonů a neutronů. Významem odpovídají izotopům chemických prvků. se tak sníží o 2, nukleonové čísloNukleonové číslo A – udává počet nukleonů (neutronů a protonů) v atomovém jádře prvku. se zmenší o 4. Jiným příkladem může být ß-rozpad, při kterém se neutron v jádře rozpadne na proton, který v jádře zůstane, a elektronElektron – první objevená elementární částice. Je stabilní. Hmotnost má 9,1×10−31 kg a elektrický náboj 1,6×10−19 C. Elektron objevil sir Joseph John Thomson v roce 1897. Existenci antičástice k elektronu (pozitron) teoreticky předpověděl Paul Dirac v roce 1928 a objevil Carl Anderson v roce 1932., který (spolu s elektronovým antineutrinemNeutrino elektronové – částice patřící mezi leptony, vzniká spolu s pozitronem při slabých rozpadech. Jde o částici velmi malé hmotnosti, která interaguje s hmotou jen slabou interakcí, snadno proto hmotou proniká. Jeho existenci předpověděl W. Pauli v roce 1930 na základě analýzy beta rozpadu. Název neutrino mu dal Enrico Fermi po objevu neutronu v roce 1932 (v italštině znamená neutrino malý neutron). Jeho existence byla potvrzena v roce 1956 v jaderné elektrárně Savannah River v Jižní Karolíně (Frederick Reines, Clyde Cowan). ), jádro opouští. Právě na principu tohoto typu radioaktivního rozpadu je založena jedna z metod, s jejíž pomocí lze velmi přesně určit stáří chondritůMeteorit kamenný – nejběžnější skupina meteoritů tvořená převážně silikátovými minerály. Tvoří 94 % všech známých meteoritů dopadlých na Zemi. 84 % kamenných meteoritů tvoří tzv. chondrity – chemicky primitivní hmota, která se svým obsahem chemických prvků (mimo lehké prvky) blíží složení sluneční fotosféry, a tedy i složení materiálu ze kterého vznikala sluneční soustava. 8 % tvoří tzv. achondrity – meteority vzniklé obvykle kompletním přetavením chondritů. Zvláštní skupiny achondritů tvoří lunární a marsovské meteority a diferencované meteority nejasného postavení..

Řez meteoritem Allende, který dopadl v roce 1969 v Mexiku. Bílé skvrny často nepravidelného tvaru jsou vápenato-hlinité inkluze (CAI), které z prachoplynného protoplanetárního disku kondenzovaly nejdříve. Pravidelná tmavá zrna kulového tvaru jsou chondrule, které se tvořily samostatně. Prošly šokovým tavením, jehož původ není dosud přesně znám, a teprve poté byly akreovány do výsledného materiálu tvořícího chondrit. Zdroj: Bavarian Meteorite Laboratory.
Radiometrická metoda izochron
Připomeňme si nejdříve rozpadový zákon, který říká, že počet nerozpadlých jader N daného izotopu závisí na počátečním počtu jader N0 a klesá exponenciálně s časem: N = N0 e–?t, kde ? je rozpadová konstanta, která má přímý vztah k poločasu rozpadu daného izotopu.
Podstatou radiometrické metody datování meteoritů, kterou označujeme jako metodu izochron, je měření poměrů obsahu izotopů, jež si můžeme zatím obecně označit jako X, Y a Y'. Tímto označením chceme vyjádřit skutečnost, že Y a Y' jsou dva různé stabilní izotopy téhož prvku, zatímco prvek X je tvořen jádry jiného prvku, která jsou nestabilní a podléhají rozpadu, díky kterému se mění na jádra izotopu prvku Y': X › Y'.
V praxi lze k měření využít například ?-rozpadu izotopu 87Rb (X), který se mění na izotop 87Sr (Y'). Roli izotopu (Y) hraje pak izotop 86Sr. Důvodem pro takovýto výběr izotopů je skutečnost, že izotopy téhož prvku Y' a Y mají prakticky totožné chemické vlastnosti, takže jejich počáteční vzájemný poměr bude v různých minerálech dané horniny všude stejný. Jinými slovy: pokud provedeme analýzu minerálů A a B, které se nachází v téže hornině, naměříme v nich vždy stejný poměr izotopů Y'/Y, přestože každý z nich bude obecně obsahovat jiné množství prvku Y. Je tomu tak proto, že izotopy Y' a Y mají stejnou chemickou afinituChemická afinita – schopnost slučovat se s jinými látkami.. Naopak prvek X má chemické vlastnosti jiné než prvek Y, a tak bude poměr X/(Y'+Y) v minerálu A jiný než v minerálu B. (Odtud zároveň vyplývá, že radiometrická metoda datování nám poskytuje informaci o tom, kdy analyzovaný vzorek meteoritu utuhnul, tzn. od jakého okamžiku se počty jader nestabilních izotopů měnily výhradně radioaktivním rozpadem, nikoli částicovou difuzí „někam jinam“.
Jaké je množství izotopu Y' v čase měření, tedy v čase t, který zároveň označuje stáří horniny? Bude to zřejmě součet původního množství jader NY'(t = 0) a jader, které přibyly rozpadem izotopu X:
NY'(t) = NY'(t = 0) + (NX(t = 0) – NX(t)).
Člen v závorce vyjadřuje úbytek jader X (počáteční počet jader X minus dnes naměřený počet jader X), což zároveň odpovídá přírůstku jader izotopu Y', na který se X rozpadá. Počáteční počet jader NX(t=0) můžeme vyjádřit z rozpadového zákona NX(t=0) = NX(t)/e–?t a získáme tak lineární rovnici:
NY'(t) = NY'(t = 0) + (e?t – 1)NX(t).
Počítat jádra daných izotopů ve vzorku je samozřejmě nesmysl, ale můžeme si pomoci měřením poměrů obsahů izotopů ?Y' = NY'/NY a ?X = NX/NY. Poměry ?Y'(t) a ?X(t) určíme měřením pomocí hmotnostního spektrometru, který pracuje na následujícím principu: vzorek materiálu zplynujeme a z volných atomů vytvoříme v ionizační komoře ionty. Ionty urychlíme v lineárním urychlovači, který působením elektrického pole urychlí na vyšší rychlosti ty ionty, které mají nižší hmotnost. Tyto ionty vystřelíme do deflektoru se silným magnetickým polem. Na nabité pohybující se částice působí v magnetickém poli Lorentzova síla, která způsobí zakřivení drah iontů. Dráhy pomalejších (a tedy těžších) iontů budou zakřiveny méně, dráhy rychlejších (a tedy lehčích) iontů budou zakřiveny více. Tím dojde k separaci iontů jednotlivých izotopů, které dopadají na různá místa detektoru. Podle množství náboje shromážděného na jednotlivých místech detektoru lze určit vzájemné poměry obsahu izotopů obsažených ve vzorku.
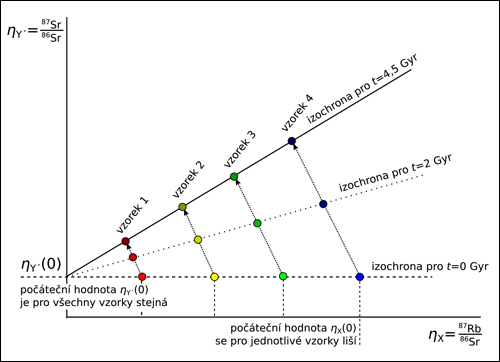
Princip metody izochron. Díky různé chemické afinitě rubidia k různým minerálům je počáteční obsah izotopu 87Rb v různých částech meteoritu různý. Chemické vlastnosti izotopů 87Sr a 86Sr jsou naopak prakticky stejné, proto je totožný i jejich počáteční poměr v daných vzorcích. Animovaný diagram [4].
Měřením tedy zjistíme poměry ?Y'(t) a ?X(t). Abychom však mohli určit z rovnice ?Y'(t) = ?Y'(t=0) + (e?t – 1)?X(t) čas t, potřebovali bychom ještě vědět, jaký byl počáteční poměr ?Y'(t=0) = Y'(t=0)/Y(t=0). Ten však bohužel neznáme. Můžeme si ale vypomoci tím, že provedeme analýzu nejméně dvou různých částí vzorku a využijeme předpokladu, že poměr ?Y(t=0) byl v různých částech vzorku stejný (viz výše), zatímco poměr ?X(t=0) se měnil. Tam, kde bylo původně větší zastoupení mateřského izotopu X, bude i v čase t větší poměr ?Y' (t) a díky lineárnímu tvaru rovnic budou body grafu ležet na přímce y = ax + b, viz obrázek. Parametry přímky a a b určíme lineární regresí. Pak bude a = e?t - 1 a b = ?Y'(t=0), takže z hodnoty a již snadno získáme stáří vzorku: t = ln(a+1)/?.
Vznik sluneční soustavy. Zdroj: NASA/YT. (mp4/h264, 36 MB).
Odkazy
- D. Nosek: Jádra a částice, řešené příklady, Matfyzpress, 2005
- M. Brož: Fyzika malých těles sluneční soustavy, Matfyzpress, 2013
- Calvin Krogman: Isochron Dating as a Current Scientific Clock; USD 2005
- Jon Fleming: Watching a Rock Age on an Isochron Diagram; TO 2002
- Wikipedia: Allende meteorite
- Jakub Rozehnal: 2012 – když vybuchne supernova; AB 9/2012
