|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Slabé měření odhaluje vlnovou funkci
Miroslav Havránek
Mikroskopické objekty, jako jsou například elementární částice, popisuje kvantová teorie pomocí vlnových funkcí. Vlnová funkce je komplexní funkcí polohy (souřadnicová reprezentace) nebo hybnosti (impulzová reprezentace). Obě reprezentace jsou navzájem převeditelné pomocí Fourierovy transformaceFourierova transformace – integrální transformace, která skládá neperiodický signál ze sinů a kosinů (resp. kmitavých komplexních exponenciál), v případě prostoročasu z rovinných vln. Původní signál (vzor) je integrálem všech parciálních signálů (obrazů). Transformace probíhá buď mezi časovou a frekvenční oblastí, nebo mezi prostoročasem a k-prostorem daným vlnovým čtyřvektorem.. Informace o kvantovém systému lze získat měřením. Měřící přístroj je na mikroskopické úrovni složen z podobných částic jako měřený objekt. Při provedení měření na kvantovém systému dojde ke změně jeho stavuKvantový stav – soubor pozorovatelných parametrů kvantového systému, kterými je systém plně charakterizován. Popis stavu musí respektovat omezení kvantové mechaniky na současnou měřitelnost či neměřitelnost veličin. Například základní energetický stav atomu značíme symbolem |S>, vakuový stav symbolem |0>, živou kočku označíme |Ž>, mrtvou kočku |M> a podobně. Kvantový stav je zpravidla charakterizován sadou kvantových čísel a je matematicky vyjádřen tzv. vlnovou funkcí (prvkem Hilbertova prostoru stavů)., systém přejde do jednoho z vlastních stavů. Vraťme se ale zpět k vlnové funkci. Vlnovou funkci lze chápat jako amplitudu pravděpodobnosti. Vlastní pravděpodobnost výskytu částice v daném prostoru nebo pravděpodobnost nalezení částice s danou hybností je rovna kvadrátu absolutní hodnoty vlnové funkce. Zatímco pravděpodobnost (reálné číslo) nalezení částice v prostoru lze experimentálně měřit, vlnovou funkci z těchto údajů zrekonstruovat nelze. Přesto se nedávno podařilo kanadským vědcům přímo změřit vlnovou funkci fotonů pomocí techniky zvané slabé měření.
|
Fourierova transformace – integrální transformace, která skládá neperiodický signál ze sinů a kosinů (resp. kmitavých komplexních exponenciál), v případě prostoročasu z rovinných vln. Původní signál (vzor) je integrálem všech parciálních signálů (obrazů). Transformace probíhá buď mezi časovou a frekvenční oblastí, nebo mezi prostoročasem a k-prostorem daným vlnovým čtyřvektorem. Půlvlnná destička – optický prvek, jehož základní charakteristikou je různá rychlost šíření světla s různou polarizací. Při vhodně zvolené tloušťce materiálu dosáhneme fázového posuvu 180 stupňů mezi dvěma vlnami se vzájemně kolmými polarizacemi. Čtvrtvlnná destička – optický prvek, jehož základní charakteristikou je různá rychlost šíření světla s různou polarizací. Při vhodně zvolené tloušťce materiálu dosáhneme fázového posuvu 90 stupňů mezi dvěma vlnami se vzájemně kolmými polarizacemi. Čtvrtvlnná destička tak může převést lineárně polarizované světlo na světlo polarizované kruhově. |
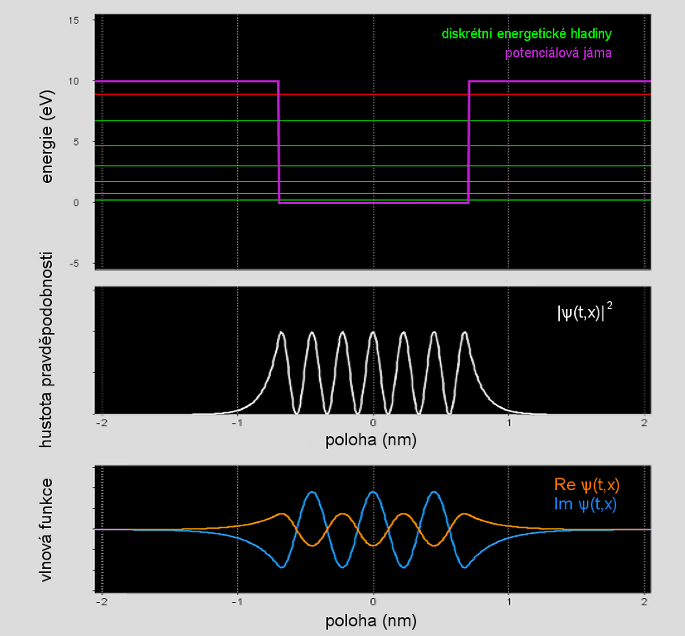
Příklad vlnové funkce částice zachycené v potenciálové jámě. Energie částice nabývá diskrétních hodnot (horní část obrázku). Hustota pravděpodobnosti výskytu částice je zobrazena ve střední části obrázku. Reálná a imaginární část vlnové funkce (v určitém čase) je vidět na spodní části obrázku. Pro vykreslení vlnové funkce byl použit stav s nejvyšší diskrétní energií (vyznačený červeně). Zdroj [3].
Slabé měření a měření vlnové funkce
S myšlenkou slabého měření přišli pánové Yakir Aharonov, David Albert a Lev Vaidman v roce 1988. Podstata slabého měření na kvantovém systému spočívá v redukci vazby mezi měřeným objektem (částicí) a měřícím přístrojem. Pokud je tato vazba velmi slabá, nedojde k narušení vlnové funkce. Za tuto výhodu platíme sníženou přesností měření. Přesnost měření je ale možné zachovat při provedení měření na mnoha systémech popsaných stejnými vlnovými funkcemi a následným zprůměrováním výsledků. Po provedení slabého měření na jednom systému můžeme provést na stejném systému další „ostré“ měření jiné veličiny, které není ovlivněno předcházejícím měřením. Zatímco výsledek ostrého měření je vlastní číslo operátoru dané veličiny (reálné číslo), výsledek slabého měření může být komplexní. Pokud při prvním (slabém) měření měříme polohu a při druhém měření hybnost, je výsledek přímo úměrný vlnové funkci. Tyto vlastnosti slabých měření využili vědci v Národním ústavu pro měřicí standardy NRC (National Research Council) v Kanadě pro měření transverzální (příčné) vlnové funkce fotonůFoton – základní kvantum energie elektromagnetického záření, polní částice elektromagnetické interakce. Má nulovou klidovou hmotnost a nemá elektrický náboj. Jeho energie a hybnost jsou přímo úměrné frekvenci záření (E = ħω, p = E/c). Stav fotonu zahrnuje také polarizaci, protože jde o příčné vlnění. Kvantování energie poprvé zavedl Max Planck při pokusech o vysvětlení záření černého tělesa. Albert Einstein dal těmto kvantům reálný význam v roce 1905 při vysvětlení fotoelektrického jevu. Samotný název foton poprvé pro tuto částici použil až americký fyzikální chemik Gilbert Lewis v dopise časopisu Nature z roku 1926.. Schéma experimentu je zobrazeno na obrázku níže.
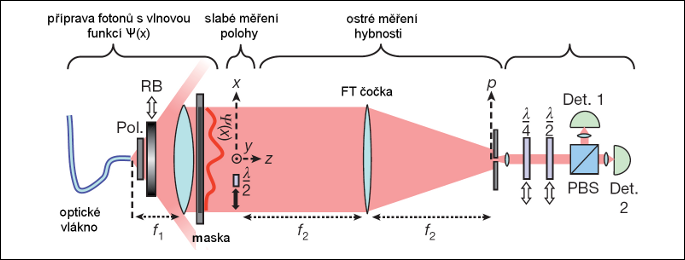
Schéma zařízení pro měření transverzální vlnové funkce fotonu. Zdroj [1].
Zdrojem fotonů je laser generující záření o vlnové délce 783 nebo 800 nm. Záření je přiváděno jednomodovým optickým vláknem do přístroje, kde projde polarizačním filtrem definujícím jeho polarizaciPolarizace světla – jde o vlastnost, pomocí níž popisujeme určitou chaotičnost světla. Elektromagnetické záření je příčným vlněním, které lze ve vakuu popsat kmity vektorů E a B kolmých na sebe a na směr šíření vlny. U nepolarizované vlny opisují koncové body obou vektorů chaotické křivky. U polarizovaného světla je naproti tomu průmět obou vektorů do roviny kolmé na směr šíření vlny přesně definován. Podle tohoto průmětu pak rozlišujeme polarizaci rovinnou, kruhovou, a eliptickou. Polarizaci posuzujeme dohodou podle roviny kmitů elektrického vektoru. Při kruhové polarizaci opisuje konec elektrického vektoru v prostoru kružnici. Příkladem polarizovaného záření je například záření odražené od rovinného zrcadla.. Světlo dále prochází čočkou a maskou o rozměrech 43×11 mm, která původní gaussovský svazek patřičně „ořeže“ a definuje tak vlnovou funkci fotonu. Vlastní slabé měření se uskutečňuje posouváním stříbrné půlvlnné destičky ve směru x. Informace o poloze fotonu je tak „zakódována“ do jeho polarizace. Vzájemnou rotací vstupního polarizačního filtru a půlvlnné destičky lze regulovat stupeň vazby mezi měřícím přístrojem a fotonem. V případě orientace 90 stupňů provádíme ostré měření, zatímco v případě paralelní orientace se přístroj fotonu „nedotkne“. Při slabém měření byl tento úhel nastaven na 20 stupňů. Dalším krokem je ostré měření hybnosti. Světlo dále projde čočkou, která provede Fourierovu transformaci – rozklad do prostorových harmonických složek. Fotony s nulovou transverzální hybností jsou zaostřeny do bodu, kde je umístěna štěrbina a další čočka. Tímto způsobem je provedena post-selekce fotonů s nulovou transverzální hybností. V další fázi tyto fotony procházejí buď čtvrtvlnnou destičkou, nebo další půlvlnnou destičkou. Polarizační rozbočovač pak rozdělí fotony podle jejich polarizace do dvou směrů, kde se nacházejí detektory. Průměrné stočení roviny polarizace, které je úměrné reálné části vlnové funkce, odpovídá poměru signálů na detektorech v případě měření s půlvlnnou destičkou. Imaginární část vlnové funkce odpovídá elipticitě kruhové polarizace, kterou lze změřit jako poměr signálů na detektorech při měření se čtvrtvlnnou destičkou. Výsledek měření je znázorněn na obrázku níže.
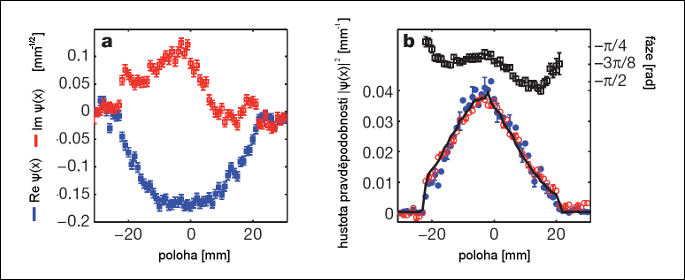
Vlevo: experimentálně změřená reálná a imaginární část vlnové funkce.
Vpravo: vyjádření vlnové funkce pomocí kvadrátu absolutní
hodnoty a fáze. Zdroj [1].
Přestože vlnová funkce byla v minulosti již měřena, je uvedená technika unikátní v tom, že se jedná o přímé měření. To znamená, že reálnou a imaginární část vlnové funkce je možné přímo odečíst z měřicího přístroje, zatímco v případě jiných metod (například kvantová tomografie) se vlnová funkce odhaduje tak, aby vyhovovala naměřeným hodnotám polohy a hybnosti. Možnost přímého měření vlnových funkcí otevírá dveře ke zkoumání stavů systémů, které mohou mít široké využití například v kvantových počítačíchKvantový počítač – počítač využívající k zápisu informace kvantově mechanické vlastnosti částic, například spin elektronů, spin atomových jader nebo jiné vlastnosti kvantově se chovajících objektů. Kvantový počítač nese současně informaci o všech možných hodnotách kvantované veličiny, a tím provádí paralelně výpočet všech možností, které mohou nastat. Výpočet je mnohonásobně efektivnější než u klasického počítače. Základní jednotka informace se nazývá qubit (kvantový bit). Zatím jsou kvantové počítače ve stádiu ověřování principů., kvantových komunikačních zařízeních pro bezpečný přenos dat a nebo v oblasti kvantové teleportace.

Část měřicího zařízení s umělecky ztvárněnou
vlnovou funkcí. Zdroj:
Jeff Lundeen
Odkazy