|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Umíme nedestruktivně detekovat jednotlivé fotony?
Petr Kulhánek
V poslední době se často objevují zprávy o nedestruktivním kvantovém měření, kdy je detekován kvantový objekt (zpravidla elektronElektron – první objevená elementární částice. Je stabilní. Hmotnost má 9,1×10−31 kg a elektrický náboj 1,6×10−19 C. Elektron objevil sir Joseph John Thomson v roce 1897. Existenci antičástice k elektronu (pozitron) teoreticky předpověděl Paul Dirac v roce 1928 a objevil Carl Anderson v roce 1932., fotonFoton – základní kvantum energie elektromagnetického záření, polní částice elektromagnetické interakce. Má nulovou klidovou hmotnost a nemá elektrický náboj. Jeho energie a hybnost jsou přímo úměrné frekvenci záření (E = ħω, p = E/c). Stav fotonu zahrnuje také polarizaci, protože jde o příčné vlnění. Kvantování energie poprvé zavedl Max Planck při pokusech o vysvětlení záření černého tělesa. Albert Einstein dal těmto kvantům reálný význam v roce 1905 při vysvětlení fotoelektrického jevu. Samotný název foton poprvé pro tuto částici použil až americký fyzikální chemik Gilbert Lewis v dopise časopisu Nature z roku 1926. nebo atomAtom – základní strukturní jednotka hmoty, jádro je složeno z neutronů a protonů, obaly z elektronů. Rozměry atomu jsou 10−10 m, rozměry jádra 10−14 m, hustota atomu je 1011 g·cm−3, hustota jádra 1014 g·cm−3. Elektrony nejsou v atomárnáím obalu lokalizovány, můžeme určit jen pravděpodobnosti jejich výskytu v tzv. orbitalech.) s minimálním narušením jeho stavuKvantový stav – soubor pozorovatelných parametrů kvantového systému, kterými je systém plně charakterizován. Popis stavu musí respektovat omezení kvantové mechaniky na současnou měřitelnost či neměřitelnost veličin. Například základní energetický stav atomu značíme symbolem |S>, vakuový stav symbolem |0>, živou kočku označíme |Ž>, mrtvou kočku |M> a podobně. Kvantový stav je zpravidla charakterizován sadou kvantových čísel a je matematicky vyjádřen tzv. vlnovou funkcí (prvkem Hilbertova prostoru stavů).. V tomto článku se budeme zabývat pokusy o nedestruktivní detekci jednotlivých fotonů, o kterou se pokouší Michel Brune se spolupracovníky na francouzské universitě Ecole Normal Supériore.
|
Kvantový stav – soubor pozorovatelných parametrů kvantového systému, kterými je systém plně charakterizován. Popis stavu musí respektovat omezení kvantové mechaniky na současnou měřitelnost či neměřitelnost veličin. Například základní energetický stav atomu značíme symbolem |S>, vakuový stav symbolem |0>, živou kočku označíme |Ž>, mrtvou kočku |M> a podobně. Kvantový stav je zpravidla charakterizován sadou kvantových čísel a je matematicky vyjádřen tzv. vlnovou funkcí (prvkem Hilbertova prostoru stavů). Fockův stav – stav v kvantové teorii, ve kterém je znám počet jedinců s danou energií. Někdy hovoříme o tzv. reprezentaci obsazovacích čísel. Tento stav je pojmenován podle sovětského fyzika Vladimira Alexandroviče Foka (1898–1974), v angličtině se jeho příjmení píše Fock. Wignerova funkce – rozdělovací funkce pro pravděpodobnost nalezení systému se souřadnicí x a hybností p ve fázovém prostoru, která odpovídá kvantové vlnové funkci ze Schrödingerovy rovnice: ρ ≈ ∫ψ*(x+y)ψ(x−y)exp[2πipy/h] dy. Rozdělení je v souladu s relacemi neurčitosti a tak Wignerova funkce popisuje přechod od kvantové teorie ke klasickým trajektoriím v mechanice. Funkce je pojmenována podle amerického fyzika Eugena Wignera (1902–1995). Rabiho frekvence – frekvence periodických změn dvouhladinového systému v přítomnosti elektromagnetického záření. Frekvence vyjadřuje intenzitu vazby mezi dvouhladinovým systémem (například atomy) a elektromagnetickým polem. Může jít například o frekvenci absorpce a stimulované reemise fotonů v dvouhladinovém systému nebo jen o frekvenci změn vlnové funkce. Frekvence je pojmenována podle rakouského fyzika Isidora Isaaca Rabiho (1898–1988). Ramseyova spektroskopie – zjištění stavu dvouhladinového systému (zpravidla atomu) za pomoci dvou interakcí s mikrovlnným pulzem (generovaným maserem). Doba mezi interakcemi je podstatně delší než doba pulzu. Stav se zjišťuje interferencí signálu z obou měření (Ramseyův interferometr). Metoda Je pojmenována podle amerického fyzika Normana Fostera Ramseye (1915), který za ni získal Nobelovu cenu v roce 1989. Rydbergův atom – atom excitovaný do vysokého hlavního a vedlejšího kvantového čísla. Rydbergovy atomy jsou velmi citlivé na okolní elektrická a magnetická pole. Elektronová vlnová funkce může být u některých superpozic stavů těchto atomů aproximována klasickým pohybem elektronu po kružnici. Vysoce excitované atomy jsou pojmenovány podle švédského fyzika Johannese Roberta Rydberga (1854–1919). |
Klasická detekce fotonů
Fotony se nejčastěji registrují klasickou nebo elektronickou cestou. Může jít o fotografickou desku či film, matici detekčních prvků CCDCCD – Charge Coupled Device, zařízení s nábojovou vazbou, umožňuje převést paralelní analogový signál (elektrický náboj kumulovaný v potenciálových jámách) na sériový signál, daný časovou posloupností proudových pulzů úměrných kumulovanému náboji. Při serializaci paralelní informace CCD funguje jako posuvný registr, který umožňuje postupné posouvání náboje změnou potenciálového profilu řízenou hodinovým signálem. (Přesun náboje si lze přestavit podobně jako řetěz lidí předávajících si při požáru na povel různě naplněná vědra s vodou. S každým povelem se konkrétní vědro posune o krok blíže k požáru. Časový průběh proudu vody vylitého do ohně odráží prostorové rozložení objemů vody ve vědrech.) Potenciálové jámy mohou být umístěny vedle sebe pouze v jediné řadě (lineární CCD) nebo ve více řadách (plošné CCD). Nejznámějšími CCD jsou fotoelektrické snímače, kdy se rozložení náboje vytváří vnitřním fotoefektem. Mohou však sloužit i jako paměťové prvky (například jako odkládací paměť pro výše zmíněné fotoelektrické snímače). V zobrazovacích zařízeních jsou nejmenší rozměry jednoho CCD pixelu 9×9 mikrometrů a plošné senzory jsou tvořeny maticí velkou až 5120×5120 pixelů. Chlazené CCD senzory pracují se šumem odpovídajícím 4 až 7 elektronům. (Údaje z roku 2008.), fotonásobičFotonásobič – často označováno jako PMT (PhotoMultiplier Tube), vakuová fotocitlivá součástka využívající zesilovacího efektu prostřednictvím sekundární emise na systému elektrod. Prvotní proud, iniciovaný dopadem světla na světlocitlivou vrstvu, fotokatodu, je tak mnohonásobně zesílen. Napětí mezi elektrodami je několik set voltů a je nastaveno tak, aby koeficient sekundární emise při dopadu elektronu na její povrch byl kladný. Fotonásobiče pracují v impulzním režimu. nebo jiné detekční zařízení. V některých detektorech jsme schopni detekovat i jednotlivé fotony, vždy to ale znamená jejich zánik. Při registraci přístrojem foton zaniká a tak lze proces měření popsat v rámci Fockových stavůFockův stav – stav v kvantové teorii, ve kterém je znám počet jedinců s danou energií. Někdy hovoříme o tzv. reprezentaci obsazovacích čísel. Tento stav je pojmenován podle sovětského fyzika Vladimira Alexandroviče Foka (1898–1974), v angličtině se jeho příjmení píše Fock. jednoduchým schématem, kdy se při měření mění jednofotonový stav ve vakuový stav:
| 1 > → | 0 >.
Klasickými detektory není možné například zjistit vznik fotonu na stěně mikrovlnné dutiny, jeho šíření prostorem a jeho následný zánik. Kvantové skoky elektromagnetického pole v dutině způsobené kreací a anihilací fotonů na stěnách dutiny jsou pro tato zařízení nedostupná.

Fotonásobič. Na levé straně je fotocitlivá katoda emitující elektrony, jejichž počet roste v jedenáctistupňovém násobiči na pravé straně. Zdroj: The National Valve Museum.
Nedestruktivní detekce
Změřit přesně polohu a hybnost fotonu není možné, brání tomu Heisenbergovy relace neurčitosti. Měření jedné veličiny ovlivní měření veličiny druhé. V principu je ale možné určit alespoň přítomnost fotonu, tj. provést nedestruktivní měření Fockova stavu
| 1 > → | 1 >.
Způsob, jak to udělat, navrhla francouzská skupina vedená Michelem Brunem již v roce 1990. K realizaci bylo ale třeba dlouhých sedmnácti let. Srdcem experimentu je mikrovlnná dutina ochlazená na teplotu 0,8 K. V ní se na stěnách rodí a zanikají fotony. Dutina je opatřena dokonale opracovanými měděnými zrcadly s přesností na 8 nanometrů, které odráží fotony mezi sebou. Zrcadla jsou potažena niobemNiob – Niobium, přechodový kovový prvek, který nachází využití v elektronice a metalurgii při výrobě speciálních slitin. Při teplotách nižších než 9,26 K a magnetických polích pod 410 mT je supravodivý. Niob byl objeven roku 1801 Charlesem Hatchttem v minerálu kolumbitu a byl pojmenován podle Niobe, dcery bájného krále Tantala.. Ten je za teploty v dutině supravodivý. Pokud se v dutině objeví foton, odrazí se od zrcadel 1,3 miliardkrát, než se rozptýlí. Přesněji, v dutině mezi zrcadly dojde k útlumu faktorem 1/e za 1,3 miliardy odrazů, což znamená, že foton urazil vzdálenost 40 000 km rovnou obvodu Země. Doba života fotonu v dutině je tak 0,13 sekundy.

Celkový pohled na rezonanční mikrovlnnou dutinu.

Nalevo: Měděné zrcadlo dutiny. Napravo: Pokovování zrcadla niobem.
Jak ale detekovat, zda je právě v dutině foton? Základní princip je na následujícím obrázku. K detekci fotonu se využívají Rydbergovy atomyRydbergův atom – atom excitovaný do vysokého hlavního a vedlejšího kvantového čísla. Rydbergovy atomy jsou velmi citlivé na okolní elektrická a magnetická pole. Elektronová vlnová funkce může být u některých superpozic stavů těchto atomů aproximována klasickým pohybem elektronu po kružnici. Vysoce excitované atomy jsou pojmenovány podle švédského fyzika Johannese Roberta Rydberga (1854–1919). rubidia Rb 85. Jsou připraveny ve stavech s vysokým hlavním kvantovým číslemKvantové číslo, hlavní – značíme n, čísluje energii systému En. Hodnota energie závisí na průběhu potenciální energie. Energie je proto jinak kvantována ve vodíkovém atomu, jinak v harmonickém oscilátoru, kvantové jámě, atd. n. Jedná se o dvoustavový systém se stavy | g >, | e > odpovídajícími číslům n = 50 a n = 51. Vedlejší kvantové čísloKvantové číslo, vedlejší – značíme l, vyjadřuje maximální možnou projekci momentu hybnosti do nějaké osy v jednotkách redukované Planckovy konstanty. U atomu vodíku nabývá vedlejší kvantové číslo hodnot 0, 1, ... n–1. Časté je označování vedlejšího kvantového čísla písmeny s, p, d, f..., které odpovídají hodnotám 0, 1, 2, 3... Velikost momentu hybnosti (nikoli projekce) je dána vztahem L2 = l(l+1)ħ2. dosahuje své maximální hodnoty l = n – 1. Frekvence odpovídající přechodu mezi oběma hladinami je 51,099 GHz. U takto vysoké excitace se elektronové orbitalyOrbital – oblast v atomárním či molekulárním obalu, kde se vyskytuje elektron. Pravděpodobnost výskytu elektronu v orbitalu je rovna druhé mocnině velikosti komplexní vlnové funkce. podobají klasickým trajektoriím a proto je možné Rydbergovy atomy považovat za kruhové útvary (tak jsou znázorněny i na obrázku).
Rydbergovy kruhové atomy mají velký dipólový moment a proto jsou mimořádně citlivé na přítomnost elektromagnetického pole. Při průchodu ultrachladnou mikrovlnnou dutinou dochází ke změně jejich vlnové funkce podle toho, zda je či není přítomen foton. V přítomnosti fotonu bude většina atomů v dutině ve stavu | e >, bez přítomnosti fotonu ve stavu | g >. Stav Rydbergových atomů lze měřit Ramseyovým spektrometremRamseyova spektroskopie – zjištění stavu dvouhladinového systému (zpravidla atomu) za pomoci dvou interakcí s mikrovlnným pulzem (generovaným maserem). Doba mezi interakcemi je podstatně delší než doba pulzu. Stav se zjišťuje interferencí signálu z obou měření (Ramseyův interferometr). Metoda Je pojmenována podle amerického fyzika Normana Fostera Ramseye (1915), který za ni získal Nobelovu cenu v roce 1989., jehož jedno rameno je před dutinou a druhé za dutinou (na obrázku jsou ramena označena R1 a R2). Oba signály se skládají do výsledného interferenčního obrazce, ze kterého je možné určit stav Rydbergových dvouhladinových atomů a tím přítomnost či nepřítomnost fotonu v dutině. Poznamenejme ještě, že míru interakce Rydbergových atomůRydbergův atom – atom excitovaný do vysokého hlavního a vedlejšího kvantového čísla. Rydbergovy atomy jsou velmi citlivé na okolní elektrická a magnetická pole. Elektronová vlnová funkce může být u některých superpozic stavů těchto atomů aproximována klasickým pohybem elektronu po kružnici. Vysoce excitované atomy jsou pojmenovány podle švédského fyzika Johannese Roberta Rydberga (1854–1919). s elektromagnetickým polem dutiny určuje tzv. Rabiho frekvenceRabiho frekvence – frekvence periodických změn dvouhladinového systému v přítomnosti elektromagnetického záření. Frekvence vyjadřuje intenzitu vazby mezi dvouhladinovým systémem (například atomy) a elektromagnetickým polem. Může jít například o frekvenci absorpce a stimulované reemise fotonů v dvouhladinovém systému nebo jen o frekvenci změn vlnové funkce. Frekvence je pojmenována podle rakouského fyzika Isidora Isaaca Rabiho (1898–1988).. Za teploty 0,8 K je 50 % šance, že v dutině je právě jeden foton a 50 % šance, že zde není foton žádný.
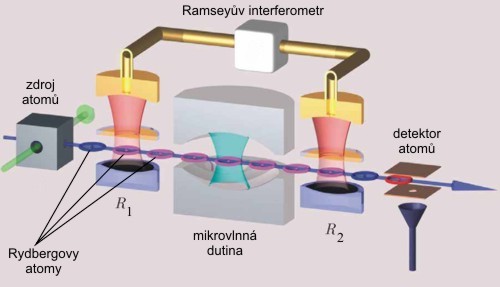
Základní schéma detekce fotonu v mikrovlnné dutině.
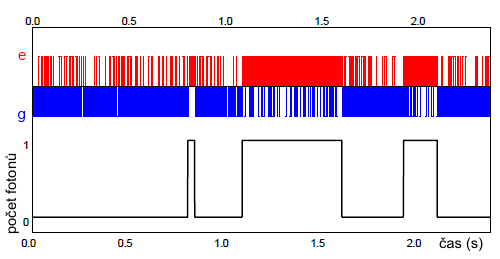
Detekovaný signál z Ramseyova spektrometru. Převažující stav | e > (červeně) znamená přítomnost fotonu. Převažující stav | g > (modře) znamená nepřítomnost fotonu. Statistický charakter signálu je zřejmý.
Uvedená měření dávají svědectví o vzniku, době života a zániku fotonu v dutině. Poprvé v historii je známa existence fotonu v dutině bez jeho likvidace. Velikou výzvou do budoucna je zjištění místa výskytu fotonu v dutině, samozřejmě v rámci možností daných kvantovou teorií. Prakticky půjde o určení tzv. Wignerovy funkceWignerova funkce – rozdělovací funkce pro pravděpodobnost nalezení systému se souřadnicí x a hybností p ve fázovém prostoru, která odpovídá kvantové vlnové funkci ze Schrödingerovy rovnice: ρ ≈ ∫ψ*(x+y)ψ(x−y)exp[2πipy/h] dy. Rozdělení je v souladu s relacemi neurčitosti a tak Wignerova funkce popisuje přechod od kvantové teorie ke klasickým trajektoriím v mechanice. Funkce je pojmenována podle amerického fyzika Eugena Wignera (1902–1995). popisující pravděpodobnost výskytu fotonu ve fázovém prostoru.
Klip týdne: Tepelné záření

Tepelné záření. V animaci jsou modře znázorněny atomy a žlutě elektrony. Obě komponenty se pohybují tepelným pohybem. Při interakci elektronu s atomem dojde tu a tam k vyslání fotonu. V průběhu animace se zvyšuje teplota, chaotický pohyb se zvětšuje a stále častěji dochází k emisi fotonů. Emitované fotony mají různé vlnové délky. Nejčastěji zastoupená vlnová délka klesá s teplotou. Čím vyšší je teplota, tím kratší fotony jsou v průměru generovány (Wienův zákon). Celkový počet generovaných fotonů roste se čtvrtou mocninou teploty (Stefanův-Boltzmannův zákon). Zdroj: Chandra / Harvard University. (mpeg, 6 MB)
Odkazy
