Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. Vydavatel: AGA (Aldebaran Group for Astrophysics) Číslo 12 – vyšlo 20. března, ročník 18 (2020) © Copyright Aldebaran Group for Astrophysics Publikování nebo šíření obsahu je zakázáno. ISSN: 1214-1674, Email: bulletin@aldebaran.cz

12/2020

Koronaviry a modelování epidemií

Vladimír Scholtz, Jaroslav Julák

V souvislosti s aktuální situací jsme si dovolili připravit tento bulletin, ve kterém bychom chtěli přinést některé základní informace jak o současně aktuálním koronaviru, tak i o matematickém modelu jím způsobované epidemie a vysvětlit jeho povahu a parametry.

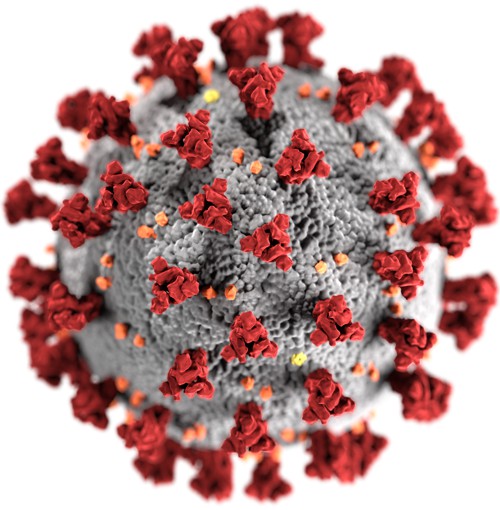
Obr. 1: Koronavirus. Zdroj: Wikimedia.org

Antigen – látka, kterou imunitní systém rozpozná jako cizorodou a reaguje na ni. Mohou to být rozpustné (solubilní) molekuly, například toxiny, nebo částice, například bakterie nebo viry. V tomto případě se jako antigeny chovají obvykle molekuly vázané na jejich povrch, jako jsou například bakteriální pouzdra nebo lipopolysacharidy. Antigeny mohou být proteiny, polysacharidy i nukleové kyseliny. Sérovar (sérotyp) – skupina mikroorganizmů jednoho druhu se společnými antigenními vlastnostmi, proti kterým si organizmus tvoří jeden typ protilátek. RNA – Ribonucleic acid, ribonukleová kyselina. Jde o nukleovou kyselinu, jejiž cukernou složkou je ribóza, nukleotidy jsou obdobné jako v DNA, pouze báze thymin je nahrazena uracilem, který také umožňuje komplementaritu s adeninem. Hlavní funkcí RNA je přenos informace z DNA do dalších struktur. Na rozdíl od DNA dvoušroubovice není typickou strukturou RNA.

Koronaviry

Čeleď Coronaviridae obsahuje RNARNA – Ribonucleic acid, ribonukleová kyselina. Jde o nukleovou kyselinu, jejiž cukernou složkou je ribóza, nukleotidy jsou obdobné jako v DNA, pouze báze thymin je nahrazena uracilem, který také umožňuje komplementaritu s adeninem. Hlavní funkcí RNA je přenos informace z DNA do dalších struktur. Na rozdíl od DNA dvoušroubovice není typickou strukturou RNA. viry rodu Betacoronavirus, způsobující obvykle lehká onemocnění podobná rýmě nebo zánětu horních cest dýchacích. V elektronovém mikroskopu mají vzhled kuliček s krásnými výběžky antigenníchAntigen – látka, kterou imunitní systém rozpozná jako cizorodou a reaguje na ni. Mohou to být rozpustné (solubilní) molekuly, například toxiny, nebo částice, například bakterie nebo viry. V tomto případě se jako antigeny chovají obvykle molekuly vázané na jejich povrch, jako jsou například bakteriální pouzdra nebo lipopolysacharidy. Antigeny mohou být proteiny, polysacharidy i nukleové kyseliny. molekul, připomínajícími královskou korunu (corona). Běžně se vyskytují u různých živočichů, u člověka je významný lidský koronavirus HuCV. Tento druh se ovšem vyskytuje v mnoha antigenních typech resp. sérovarechSérovar (sérotyp) – skupina mikroorganizmů jednoho druhu se společnými antigenními vlastnostmi, proti kterým si organizmus tvoří jeden typ protilátek., jejichž patogenita (schopnost mikrobiálního druhu vyvolat onemocnění) a virulence (schopnost daného mikroba vyvolat onemocnění) se velmi výrazně liší. Pro pochopení této situace je možné porovnání se známou analogickou a dobře prostudovanou variabilitou příbuzného chřipkového viru: u něj rozeznáváme kromě základních typů A, B a C, též řadu sérovarů daných složením povrchových antigenůAntigen – látka, kterou imunitní systém rozpozná jako cizorodou a reaguje na ni. Mohou to být rozpustné (solubilní) molekuly, například toxiny, nebo částice, například bakterie nebo viry. V tomto případě se jako antigeny chovají obvykle molekuly vázané na jejich povrch, jako jsou například bakteriální pouzdra nebo lipopolysacharidy. Antigeny mohou být proteiny, polysacharidy i nukleové kyseliny., a to hemaglutininu (16 variant) a neuraminidázy (9 variant). Jejich kombinace pak určuje antigenní typ chřipkového viru, např. H5N3. Tyto varianty pak působí různě závažná onemocnění; nejsmrtelnější byl v letech 1918–1920 původce tzv. španělské chřipky typu H1N1, který podle různých odhadů usmrtil 20–100 milionů lidí. Přesnější odhad už není možný, rozhodně však zahubil mnohem více lidí, než se povraždilo za celou 1. světovou válku. Variabilita chřipkového viru je značná, k mutaci dochází jednou za jeden replikační cyklus, každoročně proto máme „novou“ chřipku. Selekce nových typů se uskutečňuje obvykle cirkulací viru mezi ptáky (typicky kachnami), vepřem a člověkem. Tento přechod je častý při úzkém soužití těchto tří druhů, obvyklém např. v jihovýchodní Asii. Prodělané onemocnění zanechává imunitu, každý typ se ovšem antigenně odlišuje, z čehož plyne nutnost každoročního očkování proti aktuálnímu typu. Smrtnost (letalita, mortalita) chřipky není vysoká (cca 0,1–0,2 %), v důsledku častého výskytu na ni ovšem v této zemi každoročně zemře kolem 1 500 osob.

Situace lidského koronaviru je obdobná, s několika charakteristickými rysy: Jeho variabilita je zřejmě nižší, selekce virulentních (onemocnění vyvolávajících) typů je méně častá. Běžně se vyskytují málo virulentní typy NL63, OC43, NL63, HKU1 aj. V roce 2002 se v Číně objevil virus zvaný SARS-CoV, způsobující Severe Acute Respiratory Syndrome (SARS), tj. syndrom náhlého selhání dýchání. Pocházel pravděpodobně z netopýrů a přes cibetky se rychle rozšířil téměř do celého světa, onemocnělo asi 8 000 lidí, jeho smrtnost byla kolem 10 % z nakažených lidí. Další epidemii způsobil koronavirus MERS-CoV (zvaný též hCoV-EMC), poprvé pozorovaný v roce 2012 na středním Východě a způsobující Middle East Respiratory Syndrome (MERS), tj. respirační syndrom středního východu. Pocházel pravděpodobně opět z netopýrů a na člověka se přenesl přes velbloudy, kromě postižení plic způsoboval i akutní selhání ledvin, jeho vysoká smrtnost dosahovala až 50 %. Obě tato onemocnění poměrně rychle vymizela, pravděpodobně díky kratší inkubační době a vysoké smrtnosti.

Současný typ zvaný SARS-CoV-2 (též 2019-nCoV) se vyvinul opět v Číně pravděpodobně z netopýřího viru, na člověka se přenesl asi přes luskouny. Způsobuje onemocnění zvané COVID-19, manifestované v akutní fázi jako zánět plic. Pro šíření infekce je významné, že virus v okolním prostředí přežívá až několik dní. Inkubační doba je poměrně dlouhá, až 14 dní, nemocnost není vysoká, častý je bezpříznakový průběh. Smrtnost také není příliš vysoká: obvykle 1–3 %, ovšem u rizikových skupin, např. seniorů, až 18 %. Tyto skutečnosti způsobují obtíže při identifikaci nemocných resp. nosičů, při sledování průběhu šíření viru, jeho výskytu a průběhu epidemie. Kromě těchto nejistot na straně viru jsou významné též nejistoty na straně hostitele, tj. pacientů: Např. nemocnost a smrtnost se výrazně liší podle věku (děti málo, senioři více), dalšími doposud málo prostudovanými parametry jsou infekciozita (nakažlivost), nebo infekční dávka, tj. počet virových partikulí nutných k propuknutí onemocnění. Většina těchto parametrů je proměnlivá i u jiných onemocnění: např. u cholery se infekční dávka uvádí podle okolností v širokém rozmezí 10³–10⁹ bakteriálních jedinců. Tyto parametry, významné pro matematické modelování, mohou být s vyhovující přesností a spolehlivostí stanoveny dlouhodobým sledováním průběhů šíření původců epidemie a příslušných onemocnění; tento požadavek u současné pandemie ještě nemohl být splněn.

Modelování epidemií

Pro modelování epidemií existuje v současné době mnoho matematických modelů podle charakteru infekce. Tady postupnými kroky vybudujeme tzv. SIR model, který se hodí pro základní popis současné epidemie COVID-19. Cílem je populární popis tohoto modelu a jeho chování. Z toho důvodu se v dalším popisu zcela záměrně dopouštíme mnoha matematických zjednodušení, nepřesností a neúplností. Zájemce o podrobnější studium odkazujeme např. na literaturu [1].

Abychom pochopili myšlenku modelování epidemií, vyjdeme nejdříve z nejjednoduššího modelu množení organizmu v dokonale míchaném prostředí (všichni se navzájem náhodně potkávají) s neomezenými zdroji (pořád je dostatek potravy, místa a všech ostatních potřeb). V tom případě je vývoj populace závislý pouze na schopnosti organizmu se množit. Tento proces můžeme popsat jednoduchou diferenciální rovnicí

dn/dt = a·n,     a ≥ 0,

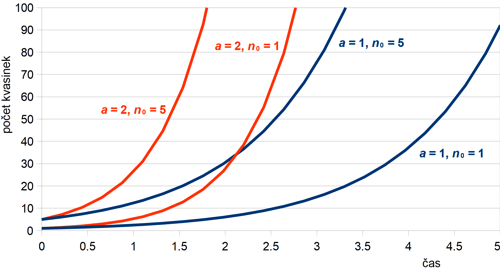
kde n je počet organizmů a koeficient a udává rychlost množení. V tomto případě nám časová změna dn/dt popisuje rychlost narůstání populace, neboli změnu počtu daného organizmu za jednotku času, což je možné přibližně zapsat i jako Δn/Δt. Tato rovnice má exponenciální řešení ve tvaru n(t) = n₀ e^at, kde n₀ je počáteční stav populace. Dá se ukázat, že tato rovnice má jeden stacionární stav, a to n₀ = 0, kdy vlastně žádné organizmy nemáme a nemá se nám tedy co množit, např. sud plně naložený švestkami, ale bez jediné kvasinky. Takto dokonale sterilní sud vydrží teoreticky nekonečně dlouho. V případě, že tam ale vložíme jen jednu jedinou kvasinku, tj. n₀ = 1, začne nám jejich počet exponenciálně narůstat. Při mitotickém (binárním přehrádečném) dělení při pokojové teplotě trvá dělicí cyklus běžné kvasinky asi 3 hodiny, tj. t_d = 180 min. Z toho dostáváme koeficient pro rychlost množení a = 2/t_d ≐ 1,9·10⁻⁴ s⁻¹ a řešení pak ve tvaru n(t) = 1 exp[1,9·10⁻⁴ t ]. Graficky je průběh řešení tohoto modelu, nazývaný i jako růstová křivka, pro dvě hezčí hodnoty a a n₀ znázorněn na obr. 2. Jak je vidět, tvar jednotlivých křivek (strmost jejich stoupání) závisí na koeficientu množení a, zatímco volbou n₀ posunujeme křivky v čase.

Obr. 2: Průběh řešení modelu růstu kvasinky bez omezení pro dvě různé hodnoty
rychlosti množení a a počáteční populace n₀.

Tato situace je samozřejmě nereálná, protože by počet kvasinek brzy přerostl všechny meze, což se experimentálně nepozoruje. Ve skutečnosti se takto exponenciálně kvasinky množí jenom ze začátku, pokud je jejich počet malý a v sudu je dostatek jak cukru, tak i místa. Mnohem realističtější pohled představuje model množení organizmů s omezením. Ten má tvar

dn/dt = a·n − b·n²,     a, b ≥ 0,

kde oproti předchozímu modelu přibyl člen tzv. párové interakce −b·n². Člen úměrný n² je možné chápat jako hodnotu přímo úměrnou pravděpodobnosti, že se nějaké dva organizmy vzájemně „potkají“. Toto setkání je možné obecně chápat jako skutečné setkání, kdy se dva jedinci potkají a třeba zápasí nebo se dělí o potravu, nebo i tak, že se třeba vyskytnou na stejném místě v různých časech, přičemž ten druhý už toto místo nalezne „vyžrané“. V našem příměru s kvasinkami v sudu švestek si tuto interakci můžeme představit jako pravděpodobnost, že se dvě kvasinky potkají u stejné molekuly cukru, přičemž ta první ji už pozřela a druhá tím pádem hladoví. Číselně je pro malé n tento člen mnohem menší než první člen a·n a systém se ze začátku vyvíjí jako v prvním modelu. Se zvyšujícím se n však tento člen začne být stále významnější a exponenciální nárůst tlumí. Grafický průběh tohoto řešení pro různé hodnoty a a b a fixní hodnotu n₀ = 1 je uveden na obr. 3. Jak je vidět z obrázku, hodnota a udává prudkost počátečního růstu populace, zatímco hodnota a/b udává konečnou hodnotu, na které se velikost populace zastaví. Také je možné odvodit, že tento systém má dva stacionární stavy (což je možné snadno ověřit dosazením), a to n_s1 = 0 a n_s2 = a/b. Podle tohoto modelu se nám populace kvasinek v sudu už nemnoží donekonečna, ale velikost její populace se ustálí na jedné stabilní hodnotě. A to už je v souladu s pozorováním. S postupem času kvasinky zdroj živin vyčerpají a promění jej v odpadní produkty, čímž dojde k jejich postupnému umírání. Tento děj už ale není v našem modelu zahrnutý.

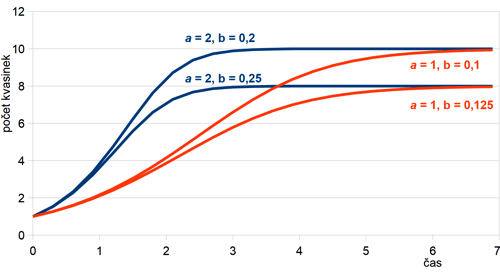
Obr. 3: Průběh řešení modelu růstu kvasinky s omezením pro různé hodnoty rychlosti
množení a a koeficientu párové interakce b, počáteční populace je n₀ = 1.

Model SI

Tento model je vhodný k popisu vývoje epidemie v konstantní (celkový počet jedinců se nemění), homogenní (všichni jedinci jsou stejní) a ideálně míchané (všichni se navzájem náhodně potkávají) populaci, přičemž samotná infekce nemá v uvažované době modelování na hostitele negativní vliv a zároveň se hostitel infekce nezbaví. Celková velikost populace činí N jedinců, kteří se dále dělí na tzv. susceptible (S) čili vnímaví, náchylní neboli zdraví a tzv. infective (I) čili infekční. Z uvedeného platí, že N = S + I. Model má tvar:

dS/dt = −r·S·I,

dI/dt = +r·S·I,

kde první rovnice vyjadřuje pokles počtu vnímavých (zdravých) jedinců, který je přes koeficient r úměrný párové interakci vnímavých a infekčních jedinců (tj. pravděpodobnost, že se potkají a že dojde k infikování). Druhá rovnice vyjadřuje nárůst počtu infekčních jedinců, který je stejný jako pokles vnímavých. Protože se celkový počet jedinců v populaci nemění, je možné druhou rovnici vyjádřit ve tvaru

dI/dt = r·N·I − r·I²,

což je stejná rovnice, jako byla ta pro množení organizmů s omezením. Průběh epidemie pro vnímavé i infekční jedince pro jednoho infekčního jedince v populaci velikosti N = 1000 je znázorněn na obr. 4. Počet infekčních jedinců ze začátku stoupá exponenciálně, poté se nárůst zmírní a ustálí se, až jsou všichni jedinci v populaci infekční; počet vnímavých jedinců je doplňkem k celkové velikosti populace.

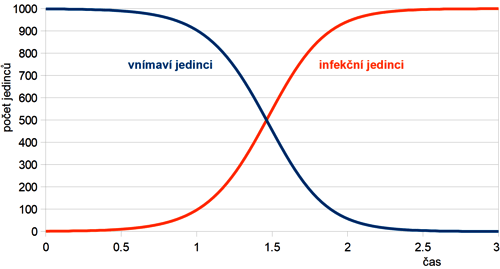
Obr. 4: Průběh řešení SI modelu v populaci N = 1000 jedinců pro koeficient
r = 0,005 a počáteční počet infekčních jedinců I₀ = 1.

Průběh vývoje infekčních jedinců pro různé hodnoty koeficientu nakažlivosti r a počátečním počtu infikovaných I₀ je znázorněn na obr. 5. Jak je vidět, s růstem r roste rychlost rozvoje epidemie, zatímco počet infekčních jedinců na začátku modelování I₀ ovlivňuje dobu, kdy k rozvoji epidemie dojde. Dále si všimněte, že model má pouze dva stacionární (finální) stavy (S = N; I = 0) a (S = 0; I = N), tj. že jsou všichni vnímaví (zdraví) a nikdo není infekční (nemocný) nebo obráceně, že všichni jsou nemocní a nikdo zdravý už nezůstal. Pokud se v populaci infekce objeví, finální stav epidemie už nezávisí na původním počtu nakažených jedinců. Na tomto počtu zavisí pouze čas, kdy k plnému propuknutí epidemie dojde.

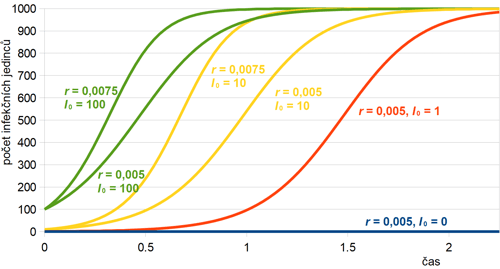
Obr. 5: Průběh řešení SI modelu pro různé hodnoty koeficientu nakažlivosti
r a počátečním počtu infikovaných I₀.

Model SIR

Tento model je rozšířením předchozího pro dlouhodobější model epidemie, kdy se počítá i s klinickým rozvinutím infekce, přičemž propuknutí infekce končí pro každého jedince buď vyléčením a získáním imunity (což je typické pro virové infekce jako chřipka nebo tato naše popisovaná) nebo smrtí (což se taky bohužel stává, ale obvykle v malých počtech). Oba tyto případy jsou v rámci populace zahrnuty do nové kategorie removed (R), čili odstraněni. Rovnice modelu jsou následující

dS/dt = −r·S·I,

dI/dt = r·S·I − a·I,

dR/dt = a·I.

První rovnice je stejná jako v předchozím případě. Ve druhé rovnici přibyl člen −a·I, který reprezentuje odstranění (tedy uzdravení se získáním imunity nebo smrt) jedince, a je přímo úměrný počtu infikovaných jedinců. Tento člen také popisuje přírůstek odstraněných jedinců ve třetí rovnici. Pokud vyjdeme z počátečního stavu populace bez infekce, tj. S = N, I = 0 a R = 0, má systém dvě stacionární (finální) řešení, a to, že epidemie buď vůbec nepropukne, tj. bude stále I = 0, nebo budou všichni jedinci v kategorii odstraněni, tj. S = 0, I = 0 a R = N (nezávisí přitom na tom, která část populace infekci přežila a která ne). Tento typický průběh epidemie je znázorněn na obr. 6, kde je vidět, že průběh kategorií náchylní a odstranění je podobný jako v předchozím modelu SI, jenom mají mezi sebou časový rozestup. V tomto čase dochází nejdříve k nárůstu počtu infikovaných jedinců a následně k jeho poklesu. Právě tento průběh je důležitý z hlediska sledování průběhu epidemie, protože nejdříve dochází k exponenciálnímu nárustu jako v případě kvasinek. Tento průběh signalizuje, že se epidemie rozvíjí a zatím nikdo neví, jak dopadne a všichni jsou nervózní. Exponenciální růst se ale následně zpomaluje, což signalizuje, že se začínáme přibližovat k vrcholu, a tudíž je vyhlídka, že epidemie může někdy skončit. Lidé, a hlavně epidemiologové, se začínají mírně uklidňovat. Poté začne počet infikovaných klesat a zdá se, že epidemie se bliží ke konci, situace se opět uklidňuje. I nadále by se měla tvrdě uplatňovat všechna opatření, aby se nezměnily parametry modelu. Vyhráno je, až je dosaženo finálního stavu.

Obr. 6: Průběh řešení SIR modelu v populaci N = 1000 jedinců pro koeficient in­fek­čnos­ti r = 0,001, odstraňování a = 0,3 a počáteční počet infekčních jedinců I₀ = 1.

Průběhy epidemie pro několik různých parametrů jsou znázorněny na obr. 7. Stejně jako v předchozím případě platí, že tvar průběhu infekce příliš nezávisí na počátečním počtu infikovaných jedinců. Tento počet ale výrazně ovlivňuje čas propuknutí epidemie. Tvar je určen pouze parametry infekčnosti r a rychlosti odstraňování a.

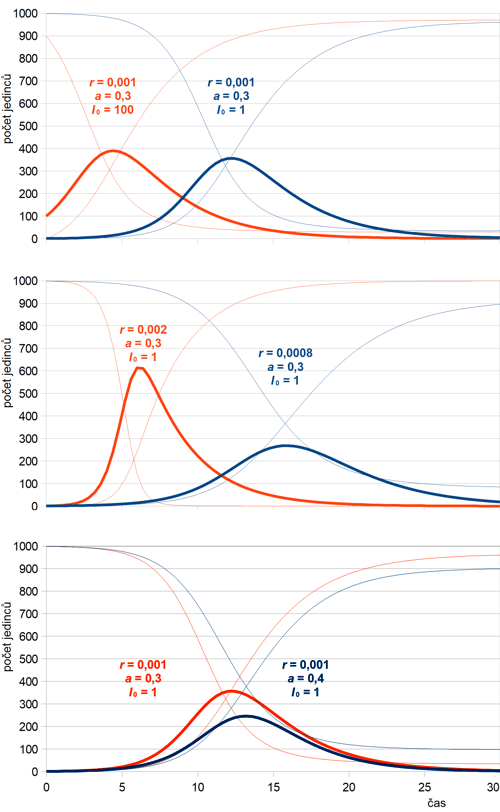
Obr. 7: Průběhy řešení SIR modelu v populaci N = 1000 jedinců pro různé koefi­cien­ty infekčnosti r, odstraňování a a počáteční počet infekčních jedinců I₀.

Tento model velice věrně popisuje některá virová onemocnění, jak je možno vidět na obr. 8, kde je zobrazen modelovaný a reálný průběh lokální epidemie chřipky na anglické chlapecké škole.

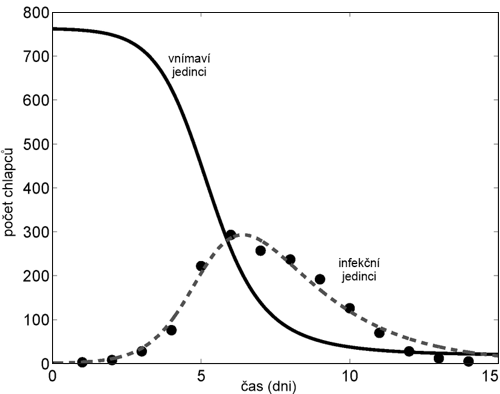
Obr. 8: SIR model (křivky) a skutečný průběh (body) epidemie chřipky na anglické
chlapecké internátní škole v roce 1978. Zdroj: [2].

A co z toho pro nás vyplývá pro COVID-19?

Jak je ale vidět z průběhů, ani jedno z předchozích opatření nezmění finální stav po­pu­lace, pouze zmírní nárůst počtu infikovaných jedinců a oddálí odeznění epi­de­mie. A proto je důležité:

*  *  *

Závěrem ještě upozornění ohledně inkubační doby 9–14 dní, která není zanesena v modelu. Model popisuje skutečný stav epidemie a počty jednotlivých skupin jedinců. To, co ale pozorujeme my, jsou typicky až jedinci, u kterých se nákaza projevila, a tudíž pozorujeme stav, který je starý zhruba těch 9–14 dnů.

*  *  *

Tento příspěvek vznikl za podpory programu Univerzity Karlovy Progress Q25.

Odkazy