|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Nové poznatky o účinnosti Faradayovy klece
Miroslav Havránek
Klec pro stínění elektrického pole vynalezl v roce 1836 jeden z nejvýznamnějších experimentátorů – Michael Faraday [1]. V dnešní době se Faradayova klec používá v mnoha obměnách ke stínění statického elektrického pole i elektromagnetických vln. Setkat se s ní můžeme například v mikrovlnné troubě, ve starších mobilních telefonech nebo ve vědeckých laboratořích. Efekt Faradayovy klece také chrání pasažéry automobilu nebo letadla před účinky zásahu bleskem. Speciální Faradayovy obleky umožňují technikům provádět opravy na vysokonapěťovém vedení pod napětím. Jen z tohoto krátkého výčtu je vidět, jak důležitou úlohu tento 179 let starý vynález hraje v našem životě. Zatímco základní princip fungování Faradayovy klece je relativně snadno pochopitelný, pokud budeme zkoumat detaily týkající se závislosti účinnosti stínění na geometrii klece, je třeba vytvořit vhodný model a použít patřičný matematický aparát k vyřešení daného problému. Je překvapivé, že neexistuje mnoho publikovaných prací zabývajících se touto problematikou. Nedávno vyšel článek [1] zabývající se matematickým popisem Faradayovy klece, který předpovídá nižší účinnost stínění, než se původně předpokládalo.

Michael Faraday byl vynikající britský experimentátor, který se zabýval elektrickými a magnetickými ději a také chemií. Mezi jeho objevy a vynálezy patří elektrolýza, elektromagnetická indukce nebo právě Faradayova klec. Zdroj: Quotation Of.
Faradayova klec
Elektricky vodivé materiály (vodiče) obsahují volné nosiče nábojů, které jsou schopny se pohybovat v materiálu pod vlivem vnějšího elektrického pole. Umístíme-li kousek vodivého materiálu do elektrického pole, dojde uvnitř tohoto vodiče k přeuspořádání nábojů. Záporný náboj se shromáždí na povrchu vodiče, blíže ke kladně nabité elektrodě, a kladný náboj blíže k záporné elektrodě. Tomuto jevu se říká elektrická indukce. Uvnitř vodiče tak vznikne indukované elektrické pole, které přesně vykompenzuje vnější elektrické pole tak, že uvnitř vodiče je pole nulové (v ideálním případě). Tento indukovaný náboj je koncentrován pouze na povrchu vodiče a vnitřní objem vodiče se stínícího efektu neúčastní. Vytvoříme-li ve vodiči dutinu, pak v ní bude rovněž nulové elektrické pole, jak je znázorněno na obrázku níže.
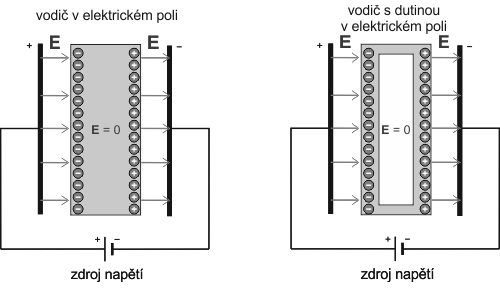
Na povrchu vodiče v elektrickém poli vznikne indukovaný náboj, který svým polem vykompenzuje elektrické pole uvnitř vodiče na nulu. Tento efekt funguje i ve vodiči s dutinou.
Stínící efekt funguje i tehdy, když vodič nemá souvislou plochu a může obsahovat otvory, případně může být složený pouze z drátů, čímž se dostáváme k Faradayově kleci. Demonstrace stínícího efektu je vidět na následujících dvou obrázcích, kde Van de Graaffův generátor vytváří statické elektrické pole, které elektrickou indukcí nabíjí tenké vodivé pásky (třásně) připevněné k testovací figurce. Tyto pásky se vlivem souhlasného náboje odpuzují. Pokud figurku umístíme do Faradayovy klece, tak je figurka umístěna v nulovém elektrickém poli (v ideálním případě) a k žádné indukci nedochází. Ovšem na povrchu Faradayovy klece existuje indukovaný náboj, jehož přítomnost signalizují vlající vodivé třásně připevněné na pravé straně klece.

Elektrické pole Van de Graaffova generátoru způsobí odpuzování
vodivých třásní připevněných k testovací figurce. Zdroj: MIT.

Faradayova klec stíní elektrické pole a k žádnému odpuzování
třásní na figurce nedochází. Zdroj: MIT.
Faradayova klec funguje i opačně – stíní elektrický náboj umístěný uvnitř a jeho elektrické pole nezasahuje ven. Klec ovšem v tomto případě musí být uzemněná (což vyplývá z Gaussova zákona pro elektrostatiku). V této konfiguraci se používá jako stínění v elektronických zařízeních, nebo v elektrických stanicích. Uzemněná Faradayova klec do značné míry stíní také elektromagnetické vlny. Zde je důležité aby vlnová délka záření byla mnohem větší než otvory v kleci (typický příklad jsou dvířka mikrovlnné trouby kde mikrovlny s vlnovou délkou 12,5 cm zůstanou uvězněny v troubě, zatímco viditelné světlo s vlnovou délkou ve stovkách nanometrů bez problému projde otvory v mřížce dvířek trouby). U elektromagnetických vln ale vstupují do hry i jiné faktory, než je vodivost klece – například permeabilita použitého materiálu.

Obří Faradayova klec stínící elektromagnetické vyzařování z transformátorů v elektrické převáděcí stanici v kalifornském Sylmaru v USA (viz mapa). Ve stanici se převádí stejnosměrné napětí 500 kV ze severozápadu USA na střídavých 230 kV při výkonu 3,1 GW. Stanice napájí velkou část Los Angeles. Povrch klece je přibližně 37 000 m2. Zdroj: Galvanizeit, Wikipedia.
Je jasné, že účinnost Fadayovy klece má své hranice. Jeden drát elektrické pole neodstíní, zatímco vodivá krabice s plnými stěnami ano. Jak tedy namodelovat přechod mezi těmito extrémními případy? Klesne intenzita elektrického pole ve Faradayově kleci skutečně na nulu? Jak závisí účinnost stínění na hustotě drátů klece?
Matematický popis Faradayovy klece
Výsledky výpočtů stínících schopností Faradayovy klece závisí na její geometrii a přesnost závisí na zjednodušeních, která se při analýze provádějí. Například analýza uváděná ve Feynmanových přednáškách ([4] – druhý díl, kapitola 7-5) uvažuje model mřížky s nekonečně tenkými a nekonečně dlouhými dráty s konstantním nábojem a předpovídá exponenciální pokles elektrického pole k nule s rostoucí vzdáleností od mřížky. Analýzou stínících schopností Faradayovy klece se nedávno také zabývala skupina matematiků na Oxfordské univerzitě. Cílem jejich studií bylo vypočítat rozložení elektrického potenciálu v okolí Faradayovy klece vyřešením Laplaceovy rovnice podobně jako ve Feynmanově případě, avšak s tím rozdílem, že vodiče mají konečný průměr a konstantní potenciál (nikoliv konstantní náboj). Zdrojem elektrického pole je elektrický náboj umístěný vně klece. Dráty klece ve dvou dimenzích reprezentuje n vodivých disků o poloměru r rozmístěných po obvodu kruhu o jednotkovém poloměru. Ekvipotenciály elektrického pole získané numerickým řešením jsou znázorněny na obrázcích níže pro několik různých poloměrů drátů a pro různé počty drátů tvořících klec.
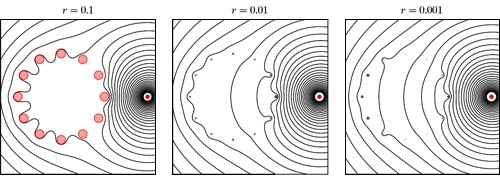
Výstup z 2D simulace elektrického potenciálu v okolí Faradayovy klece. Elektrický náboj je umístěn v pravé části každého obrázku a Faradayovu klec znázorňují růžové kruhy. Simulace byla provedena s různými průměry drátů. Je vidět, že při malém průměru drátů (obrázek zcela vpravo) efektivita stínění dramaticky klesá. Zdroj: [2].
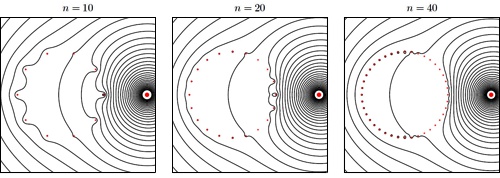
Obdobná simulace elektrického potenciálu jako na obrázku výše. Tentokrát se však mění počet drátů, které tvoří klec. Při nízkém počtu drátů elektrické pole rovněž proniká dovnitř klece. Zdroj: [2].
Elektrické pole vždy částečně proniká do klece a nikdy neklesne zcela na nulu, ale na konečnou hodnotu. Pole uvnitř klece má pouze logaritmickou závislost na poloměru drátů oproti očekávané exponenciální (což je Feynmanův případ s mřížkou s konstantním nábojem) a hyperbolickou závislost na počtu drátů. Intenzita elektrického pole uvnitř klece klesá nikoli k nule, ale ke konečně malé hodnotě pole. Tato nedokonalost stínění souvisí s indukcí náboje v drátech klece a s energií, kterou má pole kolem klece. Pro nabití tenkého drátu je potřeba více energie než pro nabití tlustého drátu na stejný náboj, protože v tenčím drátě jsou souhlasné náboje blíže sobě. Tento energetický rozdíl je zodpovědný za nedokonalou kompenzaci elektrického pole uvnitř Faradayovy klece. Výsledky simulací byly reprodukovány také pomocí jiných schémat výpočtu – například řešením Laplaceovy rovnice s nábojem spojitě rozloženým na kružnici reprezentující obvod klece nebo hledáním rozložení potenciálu pomocí minimalizace energie elektrického pole.
Závěr
Výpočty účinnosti Faradayovy klece ukazují nižší stínící schopnosti, než se doposud myslelo, což je poměrně překvapivé zjištění 179 let po jejím vynálezu – nehledě na to, že se jedná pouze o simulaci a matematický popis [2, 3]. Experimentální ověření těchto výsledků není nikterak složitý úkol a jistě by ho zvládl student fyziky nebo elektrotechniky, nicméně žádnou publikaci, která by experimentálně podpořila platnost výpočtů, se autorovi tohoto bulletinu nepodařilo dohledat. To ovšem neznamená, že by tato data nikde neexistovala. Problematika stínění je seriózní inženýrská disciplína a řeší se buď pomocí příslušného CAD softwaru, nebo jsou data o účinnosti stínící klece získána měřením pro dané geometrické uspořádání jako například v publikaci [5], což mohou být z aplikačního hlediska dostatečné údaje, ale na seriózní vědeckou publikaci pokrývající jak teoretický popis, tak experimentální data, si budeme muset asi ještě nějakou dobu počkat.
Odkazy
- L. P. Williams: Michael Faraday – British physicist and chemist, Britannica
- S. J. Chapman et al: Mathematics of the Faraday Cage, SIAM, 2015
- N. Trefethen, S. J. Chapman et al: Mathematics of the Faraday Cage, Modern Applications of Complex Variables: Modeling, Theory and Computation (workshop presentation), 2015
- R. Feynman et al: Lectures on Physics, 1963
- Holland Shielding Systems: Mu-copper Faraday cages
