|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Drake strikes back!
Jiří Hofman
Drakeova rovnice je jednoduchý předpis s mnoha neznámými faktory, pomocí něhož lze spočítat počet civilizací v Galaxii, se kterými bychom mohli komunikovat. Vymyslel ji Frank Drake v roce 1961. Obvykle se zapisuje ve tvaru:
![]()
Rovnice obsahuje sedm mezi sebou vynásobených neznámých parametrů. R je průměrný počet nově vzniklých hvězd v Galaxii, fp je podíl hvězd s planetami, ne je průměrný počet planet v planetárním systému s možností života, fl je podíl z těchto planet, kde se život opravdu vyvine, fi je dále podíl z dosud spočítaných planet, kde se vyvine inteligentní život, fc je podíl civilizací, které během své existence do Vesmíru vyšlou zachytitelné signály, a nakonec L je doba, po kterou takové civilizace tyto signály vysílají.
Samozřejmě parametr R je diskutabilní. Proč by měl počet nově vzniklých hvězd nějak úzce souviset s počtem civilizací, které můžeme kontaktovat? I z tohoto důvodu se často Drakeova rovnice vyjadřuje jako
![]()
kde Ns je počet hvězd v Galaxii a fL je podíl civilizací, které vysílaly nebo budou vysílat během doby, kdy je můžeme zachytit (zjednodušeně: vysílají právě teď). Ani tato „integrální“ forma se neobejde bez dodatečných předpokladů, nicméně pro představu, co Drakeova rovnice zahrnuje, je dostačující.
Jak lze snadno nahlédnout, Drakeův vztah je spíš hříčka než seriózní výpočet. Rovnice obsahuje parametry, z nichž některé dokážeme jen zhruba odhadnout a jiné nedokážeme odhadnout téměř vůbec. Je to spíš jen základní výčet parametrů, které výsledek zajisté ovlivňují.
Nicméně i hříčky se dají vylepšit. Claudio Maccone ji za pomoci statistiky a teorie pravděpodobnosti, zejména centrální limitní věty, změnil v robustnější předpis, který dokáže dát i zajímavé odpovědi. Výsledkem nové rovnice totiž není jen číslo, ale logaritmicko-normální rozdělení. Začněme od začátku.
Nudná statistika
Drakeova rovnice je prostý součin čísel, která známe jen velmi nepřesně. Tato nepřesnost v ní ale zahrnuta není. Hned se tedy nabízí, jak ji lze vylepšit. Každé číslo se dá nahradit náhodnou veličinou s nějakým rozdělením pravděpodobnosti. Tuto statistickou Drakeovu rovnici tak lze zapsat jako
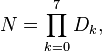
kde Dk jsou příslušné kladné náhodné veličiny. Výsledek je tedy také náhodnou veličinou. Protože součin náhodných veličin se nezpracovává snadno, je výhodné rovnici zlogaritmovat a logaritmy náhodných veličin nahradit novými náhodnými veličinami
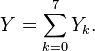
Jenže jaká rozdělení pravděpodobnosti Dk mají? Rovnou se dá vyloučit normální rozdělení, protože to vyžaduje reálnou náhodnou veličinu. Nabízí se třeba gama rozdělení, ale kvůli jednoduchosti je vhodné zvolit rovnoměrné rozdělení. Pro jeho střední hodnotu a směrodatnou odchylku platí vztahy
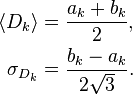
Proměnné ak a bk jsou dolní a horní meze intervalu možných hodnot Dk. Z těchto rovnic plyne, že pokud se někdy podaří stanovit střední hodnotu a směrodatnou odchylku některé Dk, její horní a dolní mez budou v našem případě od její střední hodnoty vzdáleny √3násobku směrodatné odchylky. Hustotu pravděpodobnosti náhodné veličiny Yk lze vyjádřit jako
![]()
Střední hodnota a směrodatná odchylka se pak dají vyjádřit vztahy
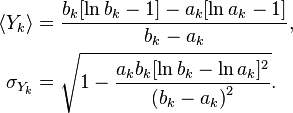
Dále poznamenejme, že hustotu pravděpodobnosti náhodné veličiny Y lze v našem případě transformovat na hustotu pravděpodobnosti náhodné veličiny N podle předpisu:
![]()
Pro následující část se bude ještě hodit výpočet charakteristické funkce náhodné veličiny Yk, tedy Fourierovy transformace výše zmíněné hustoty náhodné veličiny. Po troše integrování vyjde:
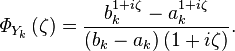
K čemu Fourierova transformace? K vyjádření hustoty pravděpodobnosti součtu náhodných veličin Yk. Hustota pravděpodobnosti součtu nezávislých náhodných veličin je totiž konvoluce jejich hustot pravděpodobnosti a zároveň konvoluce funkcí je součin jejich Fourierových transformací. Takže charakteristická funkce Y je rovna
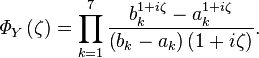
Bohužel, výpočet zpětné Fourierovy transformace není vůbec triviální a je nutno přistoupit k numerickému řešení. Postupme tedy k příkladu.
Příklad
Zvolme si nějak rozumně všechny parametry. Jde nám jen o příklad výpočtu, není tedy třeba se zabývat jejich správností.
| Dk | <Dk> | σDk |
|---|---|---|
| Ns | 3,5×1011 | 109 |
| fp | 0,5 | 0,1 |
| ne | 1 | 1/√3 |
| fl | 0,5 | 0,1 |
| fk | 0,2 | 0,1 |
| fc | 0,2 | 0,1 |
| fL | 10-6 | 10-7 |
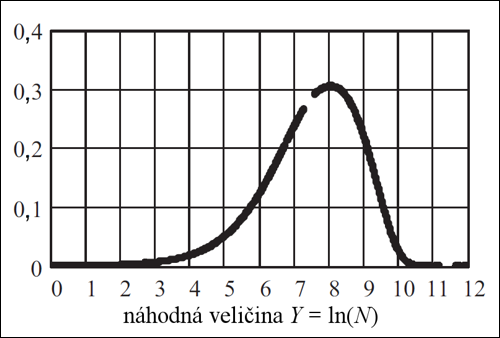
Pokud dosadíme střední hodnoty do původní Drakeovy rovnice, vyjde N = 3 500. Po numerickém výpočtu zpětné Fourierovy transformace lze hustotu pravděpodobnosti náhodné veličiny Y vyjádřit grafem:
Výsledek numerického výpočtu hustoty pravděpodobnosti náhodné veličiny Y.
Dvě přerušení grafu jsou důsledkem omezení použitého softwaru.
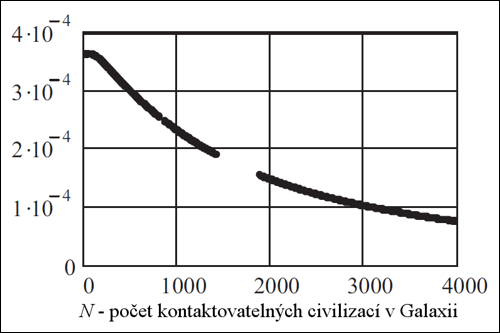
Po dalším numerickém výpočtu, tentokrát transformace hustoty pravděpodobnosti, získáme hustotu pravděpodobnosti náhodné veličiny N vyjádřenou grafem:
Hustota pravděpodobnosti náhodné veličiny N, čili toho, že v Galaxii se
nalézá N civilizací, se kterými bychom mohli komunikovat.
Z tohoto výsledku se dá pro kontrolu integrací dopočítat střední hodnota <N> = 3 500 a hlavně směrodatná odchylka. Ta vychází σN ≐ 3 953. Směrodatná odchylka je tedy větší než střední hodnota. Zde je nutno zopakovat, že tento výsledek platí pouze pro zvolené parametry a rovnoměrné rozdělení náhodných veličin Dk – není to skutečná předpověď. To, jak odpovídá obecnému řešení, ověříme v následujícím odstavci.
Zapojení centrální limitní věty
Poctivě čtoucí čtenář již možná pomalu propadal skepsi a od paniky ho ochránilo jen vědomí blízkého konce světa a smíření se s faktem, že i kdybychom do té doby nějakou mimozemskou civilizaci objevili, už si s ní moc nepopovídáme. Ještě poctivěji čtoucí čtenář ale ví, že teorie pravděpodobnosti nabízí jeden velmi silný nástroj: centrální limitní větu, kterou začátkem 20. století ve své nejobecnější verzi, ale s příliš silnými podmínkami, dokázal ruský matematik a fyzik Alexandr Michajlovič Ljapunov. Se slabšími podmínkami ji na začátku 20. let dokázal finský matematik Jarl Waldemar Lindeberg. A těm z Vás, kteří dočetli až sem, aniž by je pravděpodobnost a statistika jakkoli vzrušila, autor bulletinu nabízí aspoň jeden drb. V roce 1935 totéž dokázal ve své disertační práci na univerzitě v Cambridgi britský matematik a informatik Alan Turing nevěda, že věta je již dokázána. Práce tak ani nebyla publikována.
Ve zkratce centrální limitní věta říká, že součet náhodných veličin jakýchkoli rozdělení v limitě přechází do normálního rozdělení, přičemž jeho střední hodnota je součet středních hodnot a jeho rozptyl součtem rozptylů jednotlivých náhodných veličin.
Jeden součet, na který by se centrální limitní věta dala uplatnit, se v tomto bulletinu již objevil. Je to součet náhodných veličin Yk. Podobně jako výše i jeho výsledek můžeme transformovat. Normální rozdělení se ztransformuje na logaritmicko-normální rozdělení. Jeho vlastnosti jsou ale dobře známé:
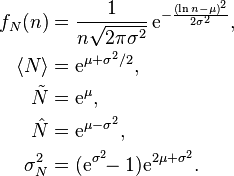
Výrazy shora dolů znamenají: hustotu pravděpodobnosti, střední hodnotu, medián, modus a rozptyl. Pokud se nyní vrátíme k příkladu, můžeme spočítat, že pro zvolené parametry je μ = 7,462 176 a σ = 1,392 381, a porovnat s výsledkem bez použití centrální limitní věty.
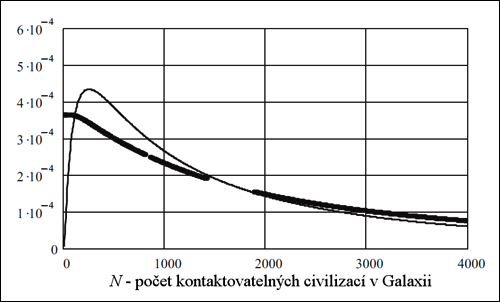
Porovnání hustot pravděpodobnosti získané bez pomoci centrální
limitní věty (tlustě) a s její pomocí (tence).
Vzhledem k tomu, že křivky jsou pro N >1 500 nápadně podobné, což je mimochodem důsledek zákona velkých čísel, můžeme se osmělit a hustotu pravděpodobnosti získanou pomocí centrální limitní věty považovat za velmi dobře nahrazující hustotu pravděpodobnosti spočítanou dříve.
Porovnejme a rozeberme ještě některé číselné výsledky. Střední hodnota je přibližně rovna 4 590. To je více, než předpovídá klasická Drakeova rovnice pro náš příklad (3 500). Pokud si můžeme dovolit zobecnění, je to jistě dobrá zpráva pro projekt SETI – civilizací je v naší Galaxii možná více, než by se na první pohled mohlo zdát. Směrodatná odchylka je zhruba 11 195. To sice může znamenat, že tu jsme sami, ale také, že se značnou pravděpodobností jsou v Galaxii až desítky tisíc civilizací, které bychom mohli nalézt. Medián je roven asi 1 740, z čehož vyplývá, že s 50 % pravděpodobností je počet civilizací v naší Galaxii v našem příkladě vyšší a se stejnou pravděpodobností nižší než toto vypočtené číslo.
Jak daleko jsou?
Získané rozdělení pravděpodobnosti může posloužit k dalším analýzám. Jednou z nich je výpočet rozdělení pravděpodobnosti vzdálenosti nejbližší mimozemské civilizace, na kterou bychom mohli, například v projektu SETI, narazit. Pro relativně jednoduchý výpočet je třeba zavést několik předpokladů. Claudio Maccone tak předpokládá, že objem Galaxie VG = πRG2hG, přičemž RG položil rovno 50 000 a hG 16 000 světelným rokům, a že civilizace jsou v Galaxii rozesety rovnoměrně. Za těchto předpokladů se dá snadno odvodit, že průměrná vzdálenost mezi dvěma civilizacemi je nepřímo úměrná třetí odmocnině počtu komunikujících civilizací v Galaxii. Trojčlenkou se dá spočítat i míra úměry C:
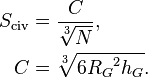
Konstanta C je přibližně rovna 28 845 světelným rokům.
Transformací hustoty pravděpodobnosti lze vyjádřit i hustotu pravděpodobnosti náhodné veličiny Sciv(r), tedy vlastně pravděpodobnost nalezení nějaké civilizace v infinitezimální kulové slupce ve vzdálenosti r:
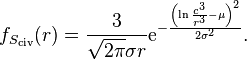
Vlastnosti této hustoty pravděpodobnosti lze také celkem snadno dopočítat:
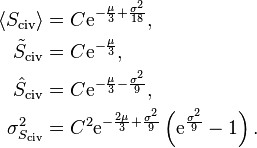
Vrátíme se opět k příkladu, do výrazů dosadíme a nakreslíme graf hustoty pravděpodobnosti. Ten prozradí další, zajímavější vlastnosti.
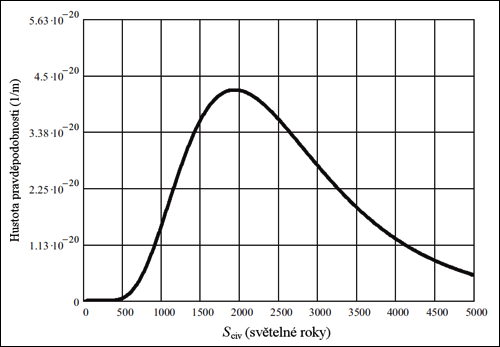
Graf pravděpodobnosti nalezení nejbližší mimozemské civilizace ve vzdálenosti r od Země.
Střední hodnota tohoto rozdělení je 2 670 světelných roků. Směrodatná odchylka 1 309 světelných roků. Se 75 % pravděpodobností tedy můžeme civilizaci očekávat v intervalu 1 361 až 3 979 světelných roků. Modus rozdělení je roven 1 933 světelným rokům – to je vzdálenost, ve které je nalezení nejbližší civilizace nejpravděpodobnější. Nutno opět podotknout, že tato čísla nejsou předpověď, vztahují se jen ke zvolenému příkladu.
Co je ale na konkrétních číslech nezávislé, je samo rozdělení, kterému se možná jednou začne říkat Macconeho. Naopak toto rozdělení je důsledkem použití centrální limitní věty. S opodstatněním jejího použití stojí a padá i následující předpověď. Na grafu pravděpodobnosti nalezení nejbližší mimozemské civilizace ve vzdálenosti r od Země je nejzajímavější část úplně vlevo, tedy to, jak popisuje naše nejbližší okolí. Pravděpodobnost nalezení cizí civilizace v našem bezprostředním okolí je podle něj prakticky nulová. I pro poměrně optimisticky zvolené parametry Drakeovy rovnice má smysl cizí civilizace hledat až ve vzdálenostech stovek či tisíců světelných roků. To je zatím mimo experimentální možnosti projektu SETI.
Není třeba smutnit nad pesimisticky vyznívajícím závěrem. Prostě se máme v projektu SETI do budoucna na co těšit. Statistická analýza kromě toho přinesla i řadu předpovědí, které jsou oproti výsledkům klasické Drakeovy rovnice pro SETI alespoň mírnou vzpruhou.
Odkazy
- C. Maccone: The Statistical Drake Equation, Acta Astronautica (2010), doi:10.1016/ j.actaastro.2010.05.003
- F. Cain: Dr. Seth Shostak Answers Your Questions About SETI
- Wikipedie: Drake equation, SETI, Log-normal distribution, Standard deviation, Probability density function, Characteristic function, Central limit theorem