Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie.
Vydavatel: AGA & Štefánikova hvězdárna v Praze
Číslo 36 (vyšlo 18. září), ročník 7 (2009)
© Copyright Aldebaran Group for Astrophysics
Publikování nebo šíření obsahu je zakázáno.
ISSN: 1214-1674,
Email: bulletin@aldebaran.cz

Hledáme hranice kvantového světa IV

Petr Kulhánek

Pojďme se dnes ještě jednou podívat do kvantového světa, který je natolik vzdálen našim běžným představám. Ve svém okolí máme zkušenosti s hmotnými objekty, které jsou lokalizované, tj. víme, kde jsou a jejich polohu jsme schopni určit měřením a toto měření je natolik jemné, že stav měřeného objektu nezmění. Setkáváme se také s některými typy vln, ať jde o často diskutované vlny na moři, zvuk či vlny elektromagnetické. Jenže svět malých rozměrů se chová úplně jinak. Objekty nemusí být lokalizované, stírá se rozdíl mezi částicí a vlnou, měření výrazně naruší stav systému, naše tělo nemá receptory schopné postihnout kvantové objekty a mozek zkušenosti vyhodnotit správně chování mikrosvěta.

Společný jmenovatel – nekomutativnost

Vznik kvantové teorie byl spletitý a rozhodně ne jednoduchý. Na počátku 20. století se experimentální úroveň lidí posunula již tak daleko, že kvantové chování látek nebylo možné opominout. Podle stávajících teorií se nedařilo vysvětlit existenci spektrálních čar, záření těles, fotoelektrický jevFotoelektrický jev – vyrážení elektronů z povrchu některých látek (zejména kovů) světlem. Při tomto jevu se projevují částicové vlastnosti světla, jednotlivý foton musí mít energii vyšší než je výstupní práce nutná k vytržení elektronu z atomu. Jev poprvé objevil Heinrich Hertz v roce 1887 a vysvětlil Albert Einstein v roce 1905., radioaktivní rozpad a dokonce ani samotnou existenci atomů. Z prvních nesmělých krůčků se před námi otevíral zcela nový svět, svět malých rozměrů s pro nás prapodivnými vlastnostmi. Vybudování prvních variant kvantové teorie trvalo čtvrt století a z dnešního pohledu se kvantový svět od našeho liší jednou základní vlastností – není komutativníKomutace – symetrická vlastnost objektů vzhledem k zavedené operaci, platí například při běžném násobení nebo sčítání čísel: AB = BA, A+B = B+A. . V makrosvětě je 3×5 = 5×3, ab = ba. V mikrosvětě tomu tak není. Pokud změříme polohu elektronuElektron – první objevená elementární částice. Je stabilní. Hmotnost má 9,1×10⁻³¹ kg a elektrický náboj 1,6×10⁻¹⁹ C. Elektron objevil sir Joseph John Thomson v roce 1897. Existenci antičástice k elektronu (pozitron) teoreticky předpověděl P. Dirac v roce 1928 a objevil C. Anderson v roce 1932. a poté jeho rychlost, dostaneme jiný výsledek, než kdybychom měření provedli v obráceném pořadí. Akt měření sám ovlivní zkoumaný objekt a změní jeho stav. Nekomutativnost je základní vlastností mikrosvěta, je mu vrozená, ať měření provádíme, či nikoli. Veškeré teorie 19. století byly komutativní, a proto při popisu mikrosvěta nutně selhaly. Teprve kvantová teorie je založena na nekomutujících matematických objektech (například maticích nebo diferenciálních operacích). A jedině nekomutativní teorie mohla odrazit vlastnosti mikrosvěta v našem vždy nedokonalém matematickém popisu skutečnosti. Poznání nekomutativnosti světa na elementární úrovni patří k nejvýznamnějším objevům v dějinách lidstva vůbec.

Z nekomutativních teorií přirozeným způsobem vyplývá kvantování některých veličin, vlnová povaha a nelokálnost objektů i nedeterminizmus v určení budoucího stavu. V podobě nekomutativních teorií lidé dostali do rukou nástroj, jehož možnosti nejsou do dnešní doby plně pochopeny. Neustále se ptáme: Kde je hranice mezi nelokálními kvantovými objekty a nám dobře známými lokalizovanými „kuličkami“? A je elektron vlna nebo částice? Otázky které, zdá se, nemají odpověď. Pokud nejsou stavyKvantový stav – soubor pozorovatelných parametrů kvantového systému, kterými je systém plně charakterizován. Popis stavu musí respektovat omezení kvantové mechaniky na současnou měřitelnost či neměřitelnost veličin. Například základní energetický stav atomu značíme symbolem |S>, vakuový stav symbolem |0>, živou kočku označíme |Ž>, mrtvou kočku |M> a podobně. Kvantový stav je zpravidla charakterizován sadou kvantových čísel a je matematicky vyjádřen tzv. vlnovou funkcí (prvkem Hilbertova prostoru stavů). objektu propleteny se stavy okolí, chová se kvantově. Pokud jsou propletené do okolí (objekt interaguje s molekulami okolního plynu, vydává záření atd.), své kvantové vlastnosti ztrácí a je možné principiálně nějakým experimentem určit jeho polohu. Hranice mezi kvantovým a naším světem tedy není pravděpodobně dána velikostí objektů, ale schopností jejich interakce s okolím (viz AB 33, 34 a 35). Snad jsme na správné stopě.

Dvojštěrbinový experiment

Dvojštěrbinový experiment byl popisován tolikrát, že se omezíme jen na jeho stručnou charakteristiku. Dvěma štěrbinami prolétá svazek částic a na stínítku jsou sledována místa jejich dopadu. Ta vytváří charakteristický interferenční obrazec, a to i tehdy, když je svazek natolik řídký, že se v prostoru interferometru nachází v průměru jedna jediná částice. To samozřejmě vede k otázkám typu: Kterým otvorem částice prolétla? Neznamená interferenční obrazec to, že prolétla oběma otvory a interferovala sama se sebou (delokalizace)? Ve snaze odpovědět na tyto otázky se můžeme pokusit zjistit polohu prolétávající částice. Jakmile ale učiníme takové kroky, aby polohu bylo možné (byť jen teoreticky) zjistit, interferenční obrazec zmizí. A právě zde je hranice mezi kvantovým a nekvantovým chováním. Principiální možnost zjistit polohu objektu, například z jeho interakce s okolím, likviduje kvantové chování. Pokud zabráníme této možnosti, můžeme pozorovat interferenci a tím kvantové chování i u obřích molekul složených z tisíců protonů a neutronů (AB 33).

Dvojštěrbina

Schrödingerova kočka

Erwin Schrödinger poukázal na absurditu aplikace kvantových vlastností na objekty makrosvěta ve známém myšlenkovém experimentu s kočkou (AB 53/2008). Kočka je uzavřena v neprůhledné krabici, kde je umístěna sklenička se smrtícím jedem. Kladivo, které skleničku rozbije, je ovládáno pomocí náhodného radioaktivního rozpadu. Po určité době je padesátiprocentní šance, že došlo k rozbití skleničky a usmrcení kočky. Dokud ale neotevřeme krabici a nepřesvědčíme se o skutečném stavu kočky, je kočka z hlediska kvantové teorie v superpozici dvou stavůKvantový stav – soubor pozorovatelných parametrů kvantového systému, kterými je systém plně charakterizován. Popis stavu musí respektovat omezení kvantové mechaniky na současnou měřitelnost či neměřitelnost veličin. Například základní energetický stav atomu značíme symbolem |S>, vakuový stav symbolem |0>, živou kočku označíme |Ž>, mrtvou kočku |M> a podobně. Kvantový stav je zpravidla charakterizován sadou kvantových čísel a je matematicky vyjádřen tzv. vlnovou funkcí (prvkem Hilbertova prostoru stavů).: „mrtvá kočka“ a „živá kočka“. Schrödinger chtěl tímto experimentem poukázat na nesmyslnost aplikace kvantových zákonů na makroskopické objekty. V experimentu se Schrödingerovou kočkou se opět setkáváme s onou pomyslnou hranicí mezi kvantovým a nekvantovým chováním: Kde končí svět kvantových objektů a začíná svět nám známých lokalizovaných objektů? Kde mizí kvantový svět? Nikdo nikdy neviděl makroskopické objekty v superpozici dvou stavů. Možná jde ale jen o technický problém jejich oddělení od okolí.

Schrodingerova kočka

Harmonický oscilátor

Velmi zajímavým systémem je harmonický oscilátor. Většina lidí si ho představuje jako kuličku na pružině nebo dvě kuličky spojené pružinkou. Obecně jde ale o jakýkoli systém s kvadratickou závislostí potenciální energie na výchylce. Síla působící na oscilátor je úměrná výchylce z rovnovážné polohy a má opačný směr. V klasické fyzice může mít harmonický oscilátor jakoukoli nezápornou energii. Harmonický oscilátor má ale širší platnost. Dokonce i elektromagnetické pole si můžeme představit jako soustavu harmonických oscilátorů. V kvantové teorii má harmonický oscilátor dvě odlišné vlastnosti od klasického oscilátoru.

Energie oscilací nemůže být libovolná, ale mění se skokem. K přechodu z jednoho vibračního stavu do jiného musíme dodat základní kvantum energie. Díky těmto přeskokům pozorujeme například vibrační spektra dvojatomárních molekul.
V klasické fyzice je nejnižší možná energie nulová a oscilátor se nepohybuje. Kvantová teorie takové řešení neumožňuje a i základní stav má nenulovou energii, která je jakýmsi nejmenším kvantem pohybu. Při absolutní nule proto neustává veškerý pohyb, ale krystaly konají tzv. nulové kmity, nejmenší možný vibrační pohyb. Absolutní nula je proto stavem těles s nejmenší možnou hodnotou energie (nikoli nulovou).

Při vysokých energiích jsou vzhledem k energii oscilátoru rozdíly energetických hladin zanedbatelné a kvantování nevnímáme. Systém tak přirozeným způsobem přechází od kvantového ke klasickému chování. Na počátku roku 2009 byly zveřejněny experimenty, které vyrážejí dech. Na makroskopickou vzdálenost bylo pozorováno propletení stavů dvou harmonických oscilátorů. Vzhledem k tomu, že propletení stavu systému s okolím je dnes považováno za klíč ke ztrátě kvantových vlastností objektu, mají tyto experimenty mimořádnou důležitost pro pochopení přechodu mezi kvantovým a klasickým světem.

Dva oscilátory

Propletení stavů dvou oscilátorů

Skupina vědců z NISTNIST – National Institute for Standards and Technology. Americký Národní úřad pro standardy a technologie. Založen byl v roce 1901. Jeho laboratoře se nacházejí v Boulderu (Colorado) a v Gaithersburgu (Maryland). v Boulderu pod vedením Johna Josta připravila makroskopicky propletené stavy dvou oscilátorů [1]. Pojďme si jejich experiment popsat. Každý oscilátor se skládal z jednoho beryliovéhoBerylium – nejlehčí prvek ze skupiny kovů alkalických zemin, tvrdý, šedý kov o značně vysoké teplotě tání. Vede špatně elektrický proud a teplo. Velmi dobře propouští radioaktivní záření. Jeho soli jsou mimořádně toxické. Berylium bylo objeveno roku 1798 Louisem Vauguelinem jako součást minerálu berylu a smaragdů. atomu ⁹Be a jednoho hořčíkovéhoHořčík – Magnesium, lehký, středně tvrdý stříbrolesklý kov, druhý nejlehčí z kovů alkalických zemin. Využívá se při výrobě lehkých a pevných slitin, jako redukční činidlo v organické syntéze a při pyrotechnických aplikacích. V léčitelství se soli hořčíku používají od 17. století. Čistý hořčík elektrolyticky připravil sir Humphry Davy roku 1808. atomu ²⁴Mg. Atomy se chovají jako kuličky spojené pružinou o délce 4 μm. Tým začal se čtyřmi kladnými ionty, které byly elektrickým polem zachyceny v potenciálové jámě. Postup přípravy propleteného stavu dvou oscilátorů je popsán v následujícím obrázku

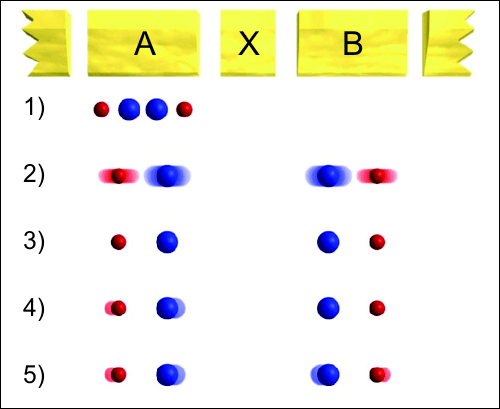
Experiment

1) Ionty jsou zachyceny v potenciálové jámě elektrického pole, která je na obrázku označena A. Ionty ⁹Be⁺ jsou červené a ionty ²⁴Mg⁺ modré. V této jámě dojde k propletení stavů obou menších iontů berylia.

2) Ionty jsou za pomoci elektrického pole přemístěny k pomocné elektrodě X a separovány do dvou párů, z nichž jeden se usadí v potenciálové jámě A a druhý v potenciálové jámě B.

3) Excitace iontů, ke které došlo pohybem je odstraněna laserovým ochlazovánímLaserové ochlazování – technika využívající k ochlazování atomů laserového světla s vlnovou délkou nepatrně nižší než je charakteristický elektronový přechod v atomu. Toto „podladění“ má za následek, ža atomy absorbují větší množství fotonů, pokud se pohybují směrem ke zdroji než pokud se pohybují od zdroje. Při interakci s fotonem atom ztrácí odpovídající hybnost ve směru zdroje světla. Při následném vyzáření fotonu sice hybnost opět získá, ale v náhodném směru. Zpravidla se používá šest laserů ve směru a proti směru tří souřadnicových os. Ať se atom vydá kamkoli, vždy proti němu bude svítit laser se správně posunutou frekvencí. Mnohonásobným opakováním lze shluk atomů ochladit na nanokelvinové teploty. V roce 1997 byla za tento objev udělena Stevenovi Chuovi, Claudeovi Cohen-Tannoudjimu a Williamovi Philipsovi Nobelova cena za fyziku.. Ionty se nacházejí v blízkosti základního stavu.

4) Laserový puls interaguje Ramanovým rozptylemRamanův jev – také Ramanův rozptyl (kombinační rozptyl, Mandelstamův rozptyl, Smekalův-Ramanův rozptyl). Jde o změnu směru i velikosti vlnového vektoru a polarizace fotonů při průchodu prostředím v důsledku interakce s vibračními a rotačními stavy molekul či krystalové mříže. Rozptýlené fotony nesou informace o energetickém spektru rozptylového centra i prostorové orientaci konkrétní chemické vazby, tedy jakési molekulární „vizitky“. Bez speciálních opatření je však tímto způsobem rozptylován pouze jediný foton ze stovek miliónů až stovek miliard dopadajících fotonů. Účinný průřez Ramanova rozptylu je zhruba 10⁻³⁰ cm². s iontem berylia v potenciálové jámě A a vytvoří propletený stav mezi spinovýmiSpin – vlastní (vnitřní) rotační moment částice souvisící s Lorentzovou symetrií. Pro částici v centrálním poli se přirozeným způsobem skládá s momentem hybnosti. Částice s nenulovým spinem se mohou chovat jako elementární magnetické dipóly μ, aniž by měly elektrický náboj. Takové částice reagují na vnější magnetická pole. a pohybovými stupni volnosti iontu.

5) Současně je spin beryliového iontu v jámě A propleten se spinem beryliového iontu v jámě B. Tím vzniká propletený stav obou oscilátorů

Skupině se podařilo vytvořit dva kvantové oscilátory, jejichž stavy byly vzájemně propleteny. Každý oscilátor měl vzdálenost obou iontů (délku pomyslné pružiny) 4 μm. Vzdálenost mezi oběma oscilátory byla 0,24 mm. Jde o natolik velikou vzdálenost, že vylučovala jakoukoli klasickou vazbu mezi oběma oscilátory. Přesto byly oscilátory spolu provázány propletením kvantových stavů na makroskopickou vzdálenost. Toto propletení stavů se podařilo udržet po dobu 100 μs. Obdobné experimenty nám umožní pochopit nelokální měření prováděná na dvou odlehlých místech současně a znamenají další krok k porozumění hranici mezi kvantovým a klasickým světem. Již dnes uvažujeme o superpozici dvou stavů makroskopických objektů na úrovni virů [2] a vracíme se tak oklikou k tomu, zda je Schrödingerova kočka mrtvá či živá.

Odkazy

Fórum – diskuze k tomuto bulletinu